甘肃省酒泉市肃州区第六片区2021-2022学年九年级上学期期末考试数学试卷
试卷更新日期:2022-01-25 类型:期末考试
一、单选题
-
1. 下列立体图形中,俯视图是三角形的是( )A、
 B、
B、 C、
C、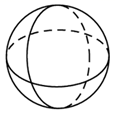 D、
D、 2. 如图,在Rt△ABC中,∠C=90°,AB=4,sinA= ,则BC的长为( )
2. 如图,在Rt△ABC中,∠C=90°,AB=4,sinA= ,则BC的长为( ) A、2 B、3 C、 D、3. 如图, ,直线a,b与 分别交于点A、B、C和点D、E、F,若AB∶BC=2∶3,EF=6,则DE的长是( )
A、2 B、3 C、 D、3. 如图, ,直线a,b与 分别交于点A、B、C和点D、E、F,若AB∶BC=2∶3,EF=6,则DE的长是( ) A、8 B、9 C、4 D、104. 一元二次方程 的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 下列四幅图的质地大小、背面图案都一样,把它们充分洗匀后翻放在桌面上,则从中任意抽取一张,抽到的图案是中心对称图形的概率是( )
A、8 B、9 C、4 D、104. 一元二次方程 的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根5. 下列四幅图的质地大小、背面图案都一样,把它们充分洗匀后翻放在桌面上,则从中任意抽取一张,抽到的图案是中心对称图形的概率是( ) A、 B、 C、 D、16. 下列性质中,菱形具有而矩形不一定具有的是( )A、对角线相等 B、对角线垂直 C、邻边垂直 D、邻角互补7. 若点A(-1, ),B(1, ),C(2, )在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,在△ABC中,点D,E分别在边AB、AC上,下列条件中不能判断△ABC∽△ADE的是( )
A、 B、 C、 D、16. 下列性质中,菱形具有而矩形不一定具有的是( )A、对角线相等 B、对角线垂直 C、邻边垂直 D、邻角互补7. 若点A(-1, ),B(1, ),C(2, )在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、8. 如图,在△ABC中,点D,E分别在边AB、AC上,下列条件中不能判断△ABC∽△ADE的是( ) A、∠ADE=∠B B、∠AED=∠C C、 D、9. 在同一坐标系中,函数 和 的图象大致是( )A、
A、∠ADE=∠B B、∠AED=∠C C、 D、9. 在同一坐标系中,函数 和 的图象大致是( )A、 B、
B、 C、
C、 D、
D、 10. 已知二次函数 的图象如图所示,在下列五个结论中:① ;② ;③ ;④ ;⑤ .其中正确的个数有( )
10. 已知二次函数 的图象如图所示,在下列五个结论中:① ;② ;③ ;④ ;⑤ .其中正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 抛物线 的顶点坐标是.12. 若反比例函数 (k≠0)的图象经过点(-1,2),则k的值是.13. 已知==≠0,则的值为
14. 在 中, , , 则 .15. 一个等腰三角形的两条边长分别是方程x2﹣7x+10=0的两根,则该等腰三角形的周长是 .16. 某厂前年缴税 万元,今年缴税 万元, 如果该厂缴税的年平均增长率为 ,那么可列方程为.17. 将一副直角三角板(含45°角的直角三角板ABC与含30°角的直角三角板DCB)按图示方式叠放,斜边交点为O,则△AOB与△COD的面积之比等于。 18. 如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .
18. 如图,点A在双曲线上,点B在双曲线y=上,且AB∥x轴,C、D在x轴上,若四边形ABCD为矩形,则它的面积为 .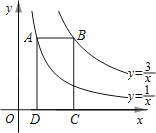
三、解答题
-
19. 计算、解方程:(1)、(2)、(3)、20. 如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
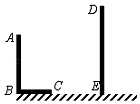 (1)、请你在图中画出此时DE在阳光下的投影;(2)、在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.21. 一个不透明的箱子里装有3个红色小球和若干个白色小球,每个小球除颜色外其他完全相同,每次把箱子里的小球摇匀后随机摸出一个小球,记下颜色后再放回箱子里,通过大量重复实验后,发现摸到红色小球的频率稳定于0.75左右.(1)、请你估计箱子里白色小球的个数;(2)、现从该箱子里摸出1个小球,记下颜色后放回箱子里,摇匀后,再摸出1个小球,求两次摸出的小球颜色恰好不同的概率(用画树状图或列表的方法).22. 在 ABC中,AD是BC边上的高,∠C=45°, ,AD=1,求BC的长.
(1)、请你在图中画出此时DE在阳光下的投影;(2)、在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.21. 一个不透明的箱子里装有3个红色小球和若干个白色小球,每个小球除颜色外其他完全相同,每次把箱子里的小球摇匀后随机摸出一个小球,记下颜色后再放回箱子里,通过大量重复实验后,发现摸到红色小球的频率稳定于0.75左右.(1)、请你估计箱子里白色小球的个数;(2)、现从该箱子里摸出1个小球,记下颜色后放回箱子里,摇匀后,再摸出1个小球,求两次摸出的小球颜色恰好不同的概率(用画树状图或列表的方法).22. 在 ABC中,AD是BC边上的高,∠C=45°, ,AD=1,求BC的长.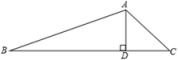 23. 如图,BD是△ABC的角平分线,过点D分别作BC和AB的平行线,交AB于点E,交BC于点F.
23. 如图,BD是△ABC的角平分线,过点D分别作BC和AB的平行线,交AB于点E,交BC于点F. (1)、求证:四边形BEDF是菱形;(2)、若AE=3,BE=4,求FC的长.24. 为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理.如图所示,正在执行巡航任务的海监船以每小时40海里的速度向正东方向航行,在A处测得灯塔P在北偏东 方向上,继续航行30分钟后到达 处,此时测得灯塔P在北偏东 方向上.
(1)、求证:四边形BEDF是菱形;(2)、若AE=3,BE=4,求FC的长.24. 为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理.如图所示,正在执行巡航任务的海监船以每小时40海里的速度向正东方向航行,在A处测得灯塔P在北偏东 方向上,继续航行30分钟后到达 处,此时测得灯塔P在北偏东 方向上.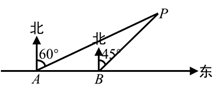 (1)、求 的度数;(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?(参考数据: , )25. 如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
(1)、求 的度数;(2)、已知在灯塔P的周围25海里内有暗礁,问海监船继续向正东方向航行是否安全?(参考数据: , )25. 如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由. 26. 已知:如图,两点 、 是一次函数 和反比例函数 图象的两个交点.
26. 已知:如图,两点 、 是一次函数 和反比例函数 图象的两个交点.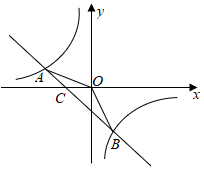 (1)、求一次函数和反比例函数的的解析式.(2)、求 的面积.(3)、观察图象,直接写出不等式 的解集.27. 喜迎元旦,某商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价每上涨1元,则每星期就会少卖出10件.(1)、假设设每件商品的售价上涨 元( 为正整数),每星期销售该商品的利润为 元,求 与 之间的函数关系式.(2)、每件商品的售价上涨多少元时,该商店每星期销售这种商品可获得最大利润?此时,该商品的定价为多少元?获得的最大利润为多少?28. 如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M.
(1)、求一次函数和反比例函数的的解析式.(2)、求 的面积.(3)、观察图象,直接写出不等式 的解集.27. 喜迎元旦,某商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价每上涨1元,则每星期就会少卖出10件.(1)、假设设每件商品的售价上涨 元( 为正整数),每星期销售该商品的利润为 元,求 与 之间的函数关系式.(2)、每件商品的售价上涨多少元时,该商店每星期销售这种商品可获得最大利润?此时,该商品的定价为多少元?获得的最大利润为多少?28. 如图,在平面直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴交于点M. (1)、求此抛物线的解析式和对称轴;(2)、在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
(1)、求此抛物线的解析式和对称轴;(2)、在此抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、连接AC,在直线AC下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.