甘肃省白银市2021-2022学年七年级上学期期末数学试卷

试卷更新日期：2022-01-25 类型：期末考试

进入出卷网下载

一、单选题

1. 在0，-4，3， $- \frac{1}{4}$ 中，最小的数是（）

A、0 B、 $- 4$ C、3 D、 $- \frac{1}{4}$

查看试题解析
2. 下列图形经过折叠可以围成一个棱柱的是（）

A、 B、 C、 D、

查看试题解析
3. 2021年“五一”假日，白银市各景点迎来旅游旺季，全市共接待境内外游客约545800人次，旅游的游客人数及收入均创历史新高，545800用科学记数法表示为（）

A、 $5.458 \times 10^{5}$ B、 $5.458 \times 10^{6}$ C、 $54.58 \times 10^{6}$ D、 $5458 \times 10^{2}$

查看试题解析
4. 下列判断错误的是（）

A、若 $a = 2$ ，则 $a + 3 = 2 + 3$ B、若 $a + 5 = b - 5$ ，则 $a = b$ C、若 $a = b$ ，则 $3 a = 3 b$ D、若 $a = b$ ，则 $\frac{a}{- 3} = \frac{b}{- 3}$

查看试题解析
5. 下列调查中最适合采用全面调查的是（）

A、调查甘肃人民春节期间的出行方式 B、调查市场上纯净水的质量 C、调查我市中小学生垃圾分类的意识 D、调查某航班上的乘客是否都持有“绿色健康码”

查看试题解析
6. 下列表述正确的是（）

A、单项式ab的系数是0，次数是2 B、 $- 2 x^{2} y^{3}$ 的系数是 $- 2$ ，次数是3 C、 $x - 1$ 是一次二项式 D、 $- a b^{2} + 3 a - 1$ 的项是 $- a b^{2}$ ，3a，1

查看试题解析
7. 下列方程中，其解为 $x = - 2$ 的是（）

A、 $3 x - 4 = 2$ B、 $3 (x + 1) - 3 = 0$ C、 $2 x = - 1$ D、 $\frac{x + 7}{5} - 1 = 0$

查看试题解析
8. 如图，观察图形，下列结论中不正确的是（）

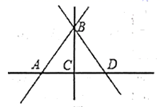A、图中有 $5$ 条线段 B、直线 $B A$ 和直线 $A B$ 是同一条直线 C、 $A B + B D > A D$ D、射线 $A C$ 和射线 $A D$ 是同一条射线

查看试题解析
9. 地铁4号线在驶进深圳北站前，列车上共有a人，停靠深圳北站后，上车人数是下车人数的3倍，列车在驶离深圳北站时车上共有b人，那么在深圳北站上车的人数有（　　）

A、（a+b）人 B、（b﹣a）人 C、 $\frac{b - a}{2}$ 人 D、 $\frac{3}{2}$ （b﹣a）人

查看试题解析
10. 如图， $∠ A O B ： ∠ B O C ： ∠ C O D = 2 ： 3 ： 4$ ，射线OM、ON分别平分 $∠ A O B$ 与 $∠ C O D$ ， $∠ M O N$ 是直角，则 $∠ C O D$ 的度数为（）

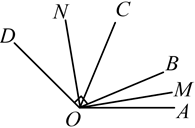A、70° B、62° C、60° D、58°

查看试题解析

二、填空题

11. $- \frac{4}{5}$ 的倒数是.

查看试题解析
12. 若 $- 2 x y^{m} + x^{n} y^{3} = - x^{n} y^{3}$ ，则 $m + n$ 的值是.

查看试题解析
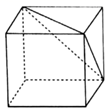
13. 一只蚂蚁从数轴上点A出发向左爬了5个单位长度到了表示-2的点处，则点A所表示的数是.

查看试题解析
14. 某市今年共有12万名考生参加中考，为了了解这12万名考生的数学成绩，从中抽取了1500名考生的数学成绩进行统计分析.在这次调查中，被抽取的1500名考生的数学成绩是.（填“总体”，“样本”或“个体”）

查看试题解析
15. 如图，一个正方体截去一个角后，剩下的几何体有条棱.

查看试题解析
16. 解一元一次方程 $\frac{1}{2} (x + 1) = 1 - \frac{1}{3} x$ 时，去分母后得到的方程是.

查看试题解析
17. 如图，一扇形纸扇完全打开后，外侧两竹条OA和OC的夹角为120°，OA的长为25cm，贴纸部分的宽AB为20cm，则一面贴纸的面积为 ${cm}^{2}$ .（结果保留π）

查看试题解析
18. 如图，这是由相同大小的正方形和相同大小的圆按照一定规律摆放而成的，按此规律，则第（n）个图形中圆的个数为.

查看试题解析

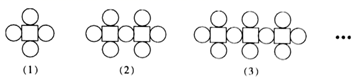
三、解答题

19. 如图，这是由5个相同的小正方体搭成的一个几何体，请画出这个几何体从左面和上面看到的形状图.

查看试题解析
20. 解方程： $6 - x = - 5 (x + 2)$ .

查看试题解析
21. 先化简，后求值：
$a^{2} - (3 a^{2} - 2 b^{2}) + 3 (a^{2} - b^{2})$ ，其中 $a = - 3 ， b = - 2$ .

查看试题解析
22. 如图，点C为线段AB的中点，点E为线段AB上的点，点D为线段AE的中点，若 $A B = 16$ ， $C E = 5$ ，求出线段AD的长度.

查看试题解析
23. 计算：

(1)、 $(- 3) - (- 2) + (- 4)$ ；

(2)、 $- 1^{4} + (- \frac{3}{2}) \times 2 - (- 4) \div \frac{1}{2}$

查看试题解析

24. 有24筐大庙香水梨，以每筐20千克为标准，超过或不足的分别用正、负来表示，记录如下：

与标准质量的差（单位：千克）	-3	-2	-1.5	0	1	2.5
筐数	1	4	4	6	5	4

请你计算这24筐香水梨的总质量是多少千克.

查看试题解析

25. 我国明代数学读本《算法统宗》一书中有这样一道题：“一支竿一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托.”其大意为：现有一根竿和一条绳索，如果用绳索去量竿，绳索比竿长5尺；如果将绳索对折后再去量竿，就比竿短5尺.设索长x尺.

(1)、用含x的式子表示竿长.

(2)、求竿长和索长.

查看试题解析
26. 如图，一块正方形纸板剪去四个相同的三角形后留下了阴影部分的图形.已知正方形的边长为a，三角形的高为h.

(1)、用含a，h的式子表示阴影部分的面积；

(2)、当 $| a - 6 | + | h - \frac{3}{2} | = 0$ 时，求阴影部分的面积.

查看试题解析
27. 在精准扶贫的政策下，某贫困户在当地政府的支持和帮助下办起了养殖业，经过一段时间的精心饲养，总量为6000只的一批兔子达到了出售标准，现从这批兔中随机选择部分进行称重，将得到的数据用下列统计图表示（频数分布直方图每组含前一个边界值，不含后一个边界值）.根据以上信息，解答下列问题：

(1)、补全图中的频数分布直方图；

(2)、估计这批兔子中质量不小于1.7kg的有多少只.

查看试题解析
28. （问题回顾）
我们曾解决过这样的问题：如图1，点O在直线 $A B$ 上， $O C$ ， $O D$ 分别平分 $∠ A O E$ ， $∠ B O E$ ，可求得 $∠ C O D = 90 °$ .（不用求解）

（问题改编）

点O在直线 $A B$ 上， $∠ C O D = 90 °$ ，OE平分 $∠ B O C$ .

(1)、如图2，若 $∠ A O C = 50 °$ ，求 $∠ D O E$ 的度数；

(2)、将图2中的 $∠ C O D$ 按图3所示的位置进行放置，写出 $∠ A O C$ 与 $∠ D O E$ 度数间的等量关系，并写明理由.

查看试题解析