海南省三亚市2021年初中学业水平模拟考试数学试卷
试卷更新日期:2022-01-25 类型:中考模拟
一、单选题
-
1. 实数2021的相反数是( )A、2021 B、-2021 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 中国互联网络信息中心数据显示,随着二胎政策全面开放,升学就业竞争压力的不断增大,满足用户碎片化学习需求的在线教育用户规模持续增长,预计2020年中国在线教育用户规模将达到305000000人.将305000000用科学记数法表示为( )A、 B、 C、 D、4. 下列四个几何体中,俯视图与其他三个不同的是( )A、
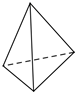 B、
B、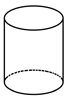 C、
C、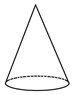 D、
D、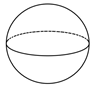 5. 已知:在直角坐标系中,点A,B的坐标分别是(1,0),(0,3),将线段AB平移,平移后点A的对应点A′的坐标是(2,﹣1),那么点B的对应点B′的坐标是( )A、(2,1) B、(2,3) C、(2,2) D、(1,2)6. 如图,将直尺与三角尺叠放在一起,如果 ,那么 的度数为( )
5. 已知:在直角坐标系中,点A,B的坐标分别是(1,0),(0,3),将线段AB平移,平移后点A的对应点A′的坐标是(2,﹣1),那么点B的对应点B′的坐标是( )A、(2,1) B、(2,3) C、(2,2) D、(1,2)6. 如图,将直尺与三角尺叠放在一起,如果 ,那么 的度数为( )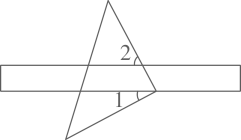 A、62° B、56° C、28° D、72°7. 将不等式组 的解集在数轴上表示,正确的是( )A、
A、62° B、56° C、28° D、72°7. 将不等式组 的解集在数轴上表示,正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 口袋里有除颜色不同其它都相同的红、黄、白三种颜色小球20个,摸到红球的概率是 , 摸到黄球的概率是 , 则袋子里有白球( )A、10个 B、4个 C、5个 D、6个9. 若反比例函数 的图象位于第二、四象限,则k的取值可能是( )A、0 B、2 C、3 D、410. 如图, 的对角线AC,BD相交于点O, 是AB中点,且AE+EO=4,则 的周长为( )
8. 口袋里有除颜色不同其它都相同的红、黄、白三种颜色小球20个,摸到红球的概率是 , 摸到黄球的概率是 , 则袋子里有白球( )A、10个 B、4个 C、5个 D、6个9. 若反比例函数 的图象位于第二、四象限,则k的取值可能是( )A、0 B、2 C、3 D、410. 如图, 的对角线AC,BD相交于点O, 是AB中点,且AE+EO=4,则 的周长为( )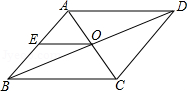 A、20 B、16 C、12 D、811. 如图,在中, , , 将绕点C逆时针转 , 得到 , 则的长是( )
A、20 B、16 C、12 D、811. 如图,在中, , , 将绕点C逆时针转 , 得到 , 则的长是( )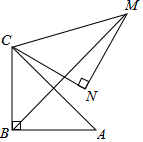 A、 B、 C、 D、12. 如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH, △CFG分别沿EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 时,则 为( )
A、 B、 C、 D、12. 如图,矩形EFGH的四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH, △CFG分别沿EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的 时,则 为( )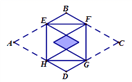 A、 B、2 C、 D、4
A、 B、2 C、 D、4二、填空题
-
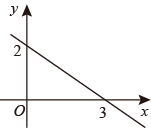
13. 比较大小:4(填“>”“<”或“=”).14. 八边形的内角和为度.15. 函数的图象如图,不等式的解集为.
 16. 如图所示,动点C在⊙O的弦AB上运动,AB=2 , 连接OC,CD⊥OC交⊙O于点D.则CD的最大值为.
16. 如图所示,动点C在⊙O的弦AB上运动,AB=2 , 连接OC,CD⊥OC交⊙O于点D.则CD的最大值为.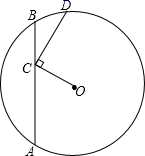
三、解答题
-
17.(1)、计算:.(2)、先化简,再求值: , 其中.18. 为响应“把中国人的饭碗牢牢端在自己手中”的号召,确保粮食安全,优选品种,提高产量,某农业科技小组对A,B两个玉米品种进行了试验种植对比研究.今年A,B两个品种各种植了10亩.收获后A,B两个品种的售价均为2.4元/千克,且B品种的平均亩产量比A品种高100千克,A,B两个品种全部售出后总收入为21600元.求A,B两个品种今年平均亩产量分别是多少千克?19. 2021年3月,中共中央、国务院颁布了《关于全面加强新时代大中小学劳动教育的意见》.某市教育局发布了“普通中小学校劳动教育状况评价指标”.为了解某校学生一周劳动次数的情况,随机抽取若干学生进行调查,得到如下统计图:
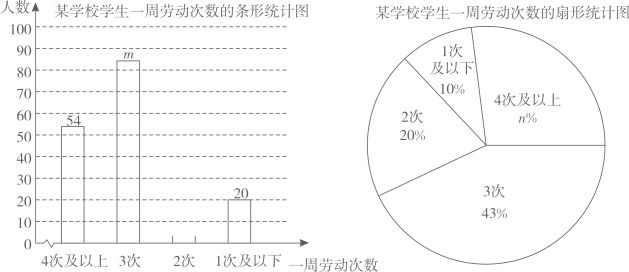 (1)、 , ;(2)、请将条形统计图补充完整;(3)、在扇形统计图中,一周劳动2次所对应的扇形圆心角为度.20. 如图,为测量一段笔直自西向东的河流的河面宽度,小明在南岸 处测得对岸 处一棵柳树位于北偏东 方向,他以每秒1.5米的速度沿着河岸向东步行40秒后到达 处,此时测得柳树位于北偏东 方向,试计算此段河面的宽度.
(1)、 , ;(2)、请将条形统计图补充完整;(3)、在扇形统计图中,一周劳动2次所对应的扇形圆心角为度.20. 如图,为测量一段笔直自西向东的河流的河面宽度,小明在南岸 处测得对岸 处一棵柳树位于北偏东 方向,他以每秒1.5米的速度沿着河岸向东步行40秒后到达 处,此时测得柳树位于北偏东 方向,试计算此段河面的宽度. 21. 如图,在矩形中, , , P为边上一点,连接 , 过点P作交于点Q,连接 , 当平分时:
21. 如图,在矩形中, , , P为边上一点,连接 , 过点P作交于点Q,连接 , 当平分时: (1)、证明:;(2)、求四边形的面积;(3)、M为直线或直线上一点,在平面内是否存在点N,使以P,C,M,N为顶点的四边形为矩形?若存在,请直接写出的长度:若不存在,请说明理由.22. 如图,已知抛物线与x轴交于点和两点,与y轴交于点C.
(1)、证明:;(2)、求四边形的面积;(3)、M为直线或直线上一点,在平面内是否存在点N,使以P,C,M,N为顶点的四边形为矩形?若存在,请直接写出的长度:若不存在,请说明理由.22. 如图,已知抛物线与x轴交于点和两点,与y轴交于点C.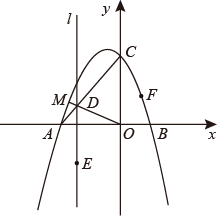 (1)、求抛物线的解析式;(2)、如图,点M为抛物线第二象限上一点,连接交线段于点D,与的面积比为.
(1)、求抛物线的解析式;(2)、如图,点M为抛物线第二象限上一点,连接交线段于点D,与的面积比为.①求点M的坐标;
②过点D作直线轴,点E是直线l上的点,点F是抛物线上一动点,是否存在这样的E、F,使得以A,C,E,F为顶点的四边形是平行四边形?若存在,求出点E,F的坐标:若不存在,请说明理由.