浙江省温州市瓯海区三校联考2021-2022学年九年级上学期12月月考数学试卷

试卷更新日期：2022-01-25 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知⊙O的半径为5，点P在⊙O外，则OP的长可能是（）

A、3 B、4 C、5 D、6

查看试题解析
2. 若 $\frac{x}{y}$ = $\frac{3}{2}$ ，则 $\frac{x}{x + y}$ 的值等于（）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{5}{2}$ D、 $\frac{5}{3}$

查看试题解析
3. 抛物线y＝﹣（x﹣1）²向右平移2个单位，平移后的抛物线的表达式为（）

A、y＝﹣（x+1）² B、y＝﹣（x﹣3）² C、y＝﹣（x﹣1）²+2 D、y＝﹣（x﹣1）²﹣2

查看试题解析
4. 下列事件是必然事件的是（）

A、任意选择某电视频道，它正在播新闻联播 B、温州今年元旦当天的最高气温为15℃ C、在装有白色和黑色的袋中摸球，摸出红球 D、不在同一直线上的三点确定一个圆

查看试题解析
5. 一种数学课本的宽与长之比为黄金比，已知它的长是26cm，那么它的宽是（）cm

A、26 $\sqrt{5}$ +26 B、26 $\sqrt{5}$ ﹣26 C、13 $\sqrt{5}$ +13 D、13 $\sqrt{5}$ ﹣13

查看试题解析
6. 在 $△$ ABC中，D，E分别是边AB，AC上的两个点，并且DE $∥$ BC，AD：BD＝3：2，则 $△$ ADE与四边形BCED的面积之比为（）

A、3：5 B、4：25 C、9：16 D、9：25

查看试题解析
7. 已知点O，C在直线m的同一侧，作⊙O交m于点A，B.连结AC，BC，OA，OB，若点C在⊙O外，∠AOB＝110°，则∠C的角度可能是（）

A、50° B、55° C、60° D、65°

查看试题解析
8. 已知三个点（﹣1，y₁），（1，y₂），（4，y₃）都在二次函数y＝x²﹣4x+c的图象上，那么y₁ ， y₂ ， y₃的大小关系正确是（）

A、y₁＜y₂＜y₃ B、y₂＜y₁＜y₃ C、y₂＜y₃＜y₁ D、y₃＜y₂＜y₁

查看试题解析
9. 在科学小实验中，一个边长为30cm正方体小木块沿着一个斜面下滑，其轴截面如图所示.初始状态，正方形的一个顶点与斜坡上的点P重合，点P的高度PF＝40cm，离斜坡底端的水平距离EF＝80cm.正方形下滑后，点B的对应点 $B$ 与初始状态的顶点A的高度相同，则正方形下滑的距离（即 $A A$ 的长度）是（）cm

A、40 B、60 C、30 $\sqrt{5}$ D、40 $\sqrt{5}$

查看试题解析
10. 已知抛物线y＝ax²﹣2ax+3不经过第四象限.当﹣1≤x≤2时，y的最大值与最小值的差是12，则a的值是（）

A、﹣3 B、3 C、4 D、12

查看试题解析

二、填空题

11. 从分别写有2，4，5，6的四张卡片中任取一张，卡片上的数是偶数的概率为.

查看试题解析
12. 线段a是线段b，c的比例中项，且b=4cm，c=9cm，则a=cm

查看试题解析
13. 已知弧的长是 $\frac{5}{3}$ π，弧的半径为3，则该弧所对的圆心角度数为°.

查看试题解析
14. 如图，已知 $△$ ABC，AB＝AC，∠A＝70°.O，D分别为BC，AB的中点，以O为圆心，OD为半径作圆，与AB的另一个交点为E，与AC交于点G，F，则∠DOE+∠FOG的度数是.

查看试题解析
15. 如图所示，草坪边上有互相垂直的小路m，n，垂足为E，草坪内有一个圆形花坛，花坛边缘有A，B，C三棵小树.在不踩踏草坪的前提下测圆形花坛的半径，某同学设计如下方案：若在小路上P，Q，K三点观测，发现均有两树与观测点在同一直线上，从E点沿着小路n往右走，测得∠1＝∠2＝∠3，EQ＝16米，QK＝24米；从E点沿着小路m往上走，测得EP＝15米，BP⊥m，则该圆的半径长为米.

查看试题解析
16. 已知抛物线y＝ax²+bx﹣5的对称轴是x＝2，与x轴的一个交点为（﹣1，0），则该抛物线与x轴的另一个交点坐标是.

查看试题解析

三、解答题

17. 如图，转盘黑色扇形和白色扇形的圆心角分别为120°和240°.

(1)、让转盘自由转动一次，指针落在白色区域的概率是多少？

(2)、让转盘自由转动两次，请用树状图或者列表法求出两次指针都落在白色区域的概率.（注：当指针恰好指在分界线上时，无效重转）

查看试题解析
18. 已知抛物线y＝﹣x²+bx+c经过点（0，1），（1，﹣4）.

(1)、求抛物线的表达式和顶点坐标.

(2)、若（﹣5，y₁），（m，y₂）是抛物线上不同的两点，且y₁+y₂＝﹣8，求m的值.

查看试题解析
19. 如图，在5×5的方格纸中，已知格点 $△$ ABC，请按要求画图.

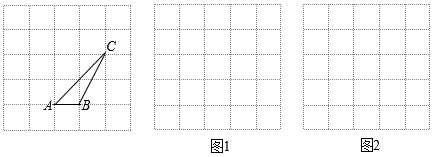(1)、在图1画一个格点 $△$ DEF，使 $△$ DEF与 $△$ ABC相似，且 $△$ DEF与 $△$ ABC的周长比是2.

(2)、在图2画一个格点 $△$ MNL，使 $△$ MNL与 $△$ ABC相似，且 $△$ MNL与 $△$ ABC的面积比是2.

查看试题解析
20. 如图，⊙O是四边形ABCD的外接圆，AD为⊙O的直径.连结BD，若 $\overset{⌢}{A C} = \overset{⌢}{B D}$ .

(1)、求证：∠1＝∠2.

(2)、当AD＝4 $\sqrt{2}$ ， BC＝4时，求 $△$ ABD的面积.

查看试题解析
21. 如图，抛物线y＝x²﹣2x+c与x轴交于A，B两点（点A在点B左侧），与y轴交于点C（0，﹣3）.

(1)、求AB的长.

(2)、将点A向上平移n个单位至点E，过点E作DF $∥$ x轴，交抛物线与点D，F.当DF＝6时，求n的值.

查看试题解析
22. 如图，矩形ABCD，BF⊥AC交CD于点E，交AD的延长线于点F.

(1)、求证：AB²＝BC•AF.

(2)、当 $\frac{B C}{A B} = \frac{2}{3}$ ， DF＝5时，求AC的长.

查看试题解析
23. 某蛋糕店有线下和网上两种销售方式，每天共销售50个。已知线下和网上销售的纯利润分别为24元/个，20元/个，每天的总纯利润为1120元.

(1)、求线下和网上的销售量分别是多少.

(2)、该店为了扩大业务，增加了销售量。调查发现，线下销售的每个蛋糕的纯利润保持不变；网上销售在原来的基础上每降低1元的纯利润，销售量增加2个.
①该店当天线下和网上销售量均为34个，求当天的总纯利润？

②若线下增加的销售量不超过原来线下销售量的 $\frac{1}{3}$ ，该店每天生产多少个蛋糕，可使当天的总纯利润最大？

查看试题解析
24. 如图1，已知 $△$ ABC，∠CAB＝45°，AB＝7，AC＝3 $\sqrt{2}$ ， CD⊥AB于点D.E是边BC上的动点，以DE为直径作⊙O，交BC为F，交AB于点G，连结DF，FG.

(1)、求证：∠BCD＝∠FDB.

(2)、当点E在线段BF上，且 $△$ DFG为等腰三角形时，求DG的长.

(3)、如图2，⊙O与CD的另一个交点为P.若射线AP经过点F，求 $\frac{A P}{D E}$ 的值.

查看试题解析