江苏省扬州市六校联盟2021-2022学年九年级上学期12月月考数学试卷
试卷更新日期:2022-01-25 类型:月考试卷
一、单选题
-
1. 已知点P在半径为1的上,则( )A、 B、 C、 D、以上答案都不正确2. 若(),下列变形正确的是( )A、 B、 C、 D、3. 二次函数的顶点坐标是( )A、 B、 C、 D、4. 如图,点A,B,C均在 上, , 则 的度数为( )
 A、 B、 C、 D、5. 如图,已知 , 若 , , , 则AC的长是( )
A、 B、 C、 D、5. 如图,已知 , 若 , , , 则AC的长是( )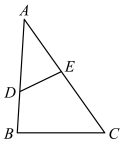 A、12 B、13 C、14 D、156. 用一个圆心角为 , 半径为12的扇形作为一个圆锥的侧面,则该圆锥底面半径为( )A、 B、4 C、6 D、87. 已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数 图象的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为( )A、0米到3米 B、5米到8米 C、到8米 D、5米到 米8. 如图,在直角坐标系中, , , , 以A为位似中心且在点A同侧,把按相似比放大,放大后的图形记作 , 则的最小值是( )
A、12 B、13 C、14 D、156. 用一个圆心角为 , 半径为12的扇形作为一个圆锥的侧面,则该圆锥底面半径为( )A、 B、4 C、6 D、87. 已知烟花弹爆炸后某个残片的空中飞行轨迹可以看成为二次函数 图象的一部分,其中x为爆炸后经过的时间(秒),y为残片离地面的高度(米),请问在爆炸后1秒到6秒之间,残片距离地面的高度范围为( )A、0米到3米 B、5米到8米 C、到8米 D、5米到 米8. 如图,在直角坐标系中, , , , 以A为位似中心且在点A同侧,把按相似比放大,放大后的图形记作 , 则的最小值是( )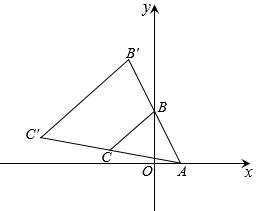 A、 B、 C、 D、3
A、 B、 C、 D、3二、填空题
-
9. 数据6,3,9,7,1的极差是.10. 已知关于x的方程有两个相等的实数根,则m的值为.11. 若点C是线段AB的黄金分割点, , 线段AC的长为2,则.(保留根号)12. 如图,一个转盘,转盘上共有红、白两种不同的颜色,已知红色区域的圆心角为 , 自由转动转盘,指针落在白色区域的概率是.
 13. 将抛物线y = x2先向右平移1个单位,再向上平移2个单位后,所得抛物线的函数表达式是.14. 如图, 中弦AB长为24,半径 于点D,若 , 则 半径长是.
13. 将抛物线y = x2先向右平移1个单位,再向上平移2个单位后,所得抛物线的函数表达式是.14. 如图, 中弦AB长为24,半径 于点D,若 , 则 半径长是. 15. , , 三点都在二次函数的图象上,则a,b,c的大小关系为.(用“<”连接)16. 如图,直线 与x轴、y轴分别交于点B、A,点C是x轴上一动点,以C为圆心, 为半径的作 , 当 与直线AB相切时,点C的坐标为.
15. , , 三点都在二次函数的图象上,则a,b,c的大小关系为.(用“<”连接)16. 如图,直线 与x轴、y轴分别交于点B、A,点C是x轴上一动点,以C为圆心, 为半径的作 , 当 与直线AB相切时,点C的坐标为. 17. 如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是.
17. 如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是. 18. 若关于x的方程在范围内有且只有一个实数根,则实数m的取值范围是.
18. 若关于x的方程在范围内有且只有一个实数根,则实数m的取值范围是.三、解答题
-
19. 解方程:(1)、;(2)、.20. 甲、乙两人在相同的情况下各打靶6次,每次打靶的成绩依次如下(单位:环):
甲:10,7,8,7,8,8
乙:5,6,10,8,9,10
(1)、甲成绩的众数 , 乙成绩的中位数.(2)、计算乙成绩的平均数和方差;(3)、已知甲成绩的方差是1环,则的射击成绩离散程度较小.(填“甲”或“乙”)21. 一张连排休息座椅设有4个座位,甲先坐在如图所示的座位上,乙、丙2人等可能地坐到①、②、③中的2个座位上. (1)、乙坐在②号座位的概率是.(2)、用画树状图或列表的方法,求乙与丙相邻而坐的概率.22. 在学校劳动基地里有一块长40米、宽20米的矩形试验田,为了管理方便,准备沿平行于两边的方向纵、横开辟三条等宽的小道,如图.已知这块矩形试验田中种植的面积为741平方米,小道的宽为多少米?
(1)、乙坐在②号座位的概率是.(2)、用画树状图或列表的方法,求乙与丙相邻而坐的概率.22. 在学校劳动基地里有一块长40米、宽20米的矩形试验田,为了管理方便,准备沿平行于两边的方向纵、横开辟三条等宽的小道,如图.已知这块矩形试验田中种植的面积为741平方米,小道的宽为多少米? 23. 如图,在四边形 中, , , 点E、F分别在AB、BC上,且 .
23. 如图,在四边形 中, , , 点E、F分别在AB、BC上,且 . (1)、求证: ;(2)、若 , , , 求BE的长.24. 已知二次函数.
(1)、求证: ;(2)、若 , , , 求BE的长.24. 已知二次函数. (1)、写出它的顶点坐标;(2)、在下图的直角坐标系中,描出5个整点(横纵坐标均为整数的点)并连线画出的它的图象;(3)、结合图象回答:
(1)、写出它的顶点坐标;(2)、在下图的直角坐标系中,描出5个整点(横纵坐标均为整数的点)并连线画出的它的图象;(3)、结合图象回答:①当时,y的取值范围是;
②当时,x的取值范围是.
25. 如图,在△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,点E为BC的中点,连接DE. (1)、求证:DE为⊙O的切线;(2)、若BC=2,∠BAC=30°,求阴影部分的面积.26. 在一次数学探究活动中,王老师设计了一份活动单:已知线段 , 使用作图工具作 , 尝试操作后思考:这样的点A唯一吗?点A的位置有什么特征?你有什么感悟?
(1)、求证:DE为⊙O的切线;(2)、若BC=2,∠BAC=30°,求阴影部分的面积.26. 在一次数学探究活动中,王老师设计了一份活动单:已知线段 , 使用作图工具作 , 尝试操作后思考:这样的点A唯一吗?点A的位置有什么特征?你有什么感悟?“追梦”学习小组通过操作、观察、讨论后汇报:点A的位置不唯一,它在以BC为弦的圆弧上(点B、C除外),….小华同学画出了符合要求的一条圆弧(如图1).
 (1)、小华同学提出了下列问题,请你帮助解决.
(1)、小华同学提出了下列问题,请你帮助解决.①该弧所在圆的半径长为;
② 面积的最大值为;
(2)、经过比对发现,小明同学所画的角的顶点不在小华所画的圆弧上,而在如图1所示的弓形外部,我们记为 , 请你利用图1证明 .(3)、请你运用所学知识,结合以上活动经验,解决问题:如图2,已知矩形 的边长 , , 点P在直线CD的左侧,且 , 则线段PB长的最小值为.27. 如图,二次函数()的图象经过点 , 点 , 点 , 连接AC. (1)、求二次函数的表达式;(2)、点P是该二次函数()图象上位于第一象限内的一点.
(1)、求二次函数的表达式;(2)、点P是该二次函数()图象上位于第一象限内的一点.①如图1,过点P作y轴的平行线交BC于点D,求线段PD的最大值.
②如图2,过点P作 , 交直线BC于点Q,若 , 求点P的坐标.
28. 某地实施产业扶贫种植某种水果,其成本经过测算为20元 , 投放市场后,经过市场调研发现,这种水果在上市的一段时间内的销售单价p(元)与时间t(天)之间的函数图象如图,且其日销售量y()与时间t(天)的关系是: , 天数为整数. (1)、试求销售单价p(元)与时间t(天)之间的函数关系式;(2)、哪一天的销售利润最大?最大日销售利润为多少?(3)、在实际销售的前28天中,公司决定每销售水果就捐赠n元利润()给“精准扶贫”对象.现发现:在前28天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
(1)、试求销售单价p(元)与时间t(天)之间的函数关系式;(2)、哪一天的销售利润最大?最大日销售利润为多少?(3)、在实际销售的前28天中,公司决定每销售水果就捐赠n元利润()给“精准扶贫”对象.现发现:在前28天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.