江苏省淮安市淮阴区2021-2022学年九年级上学期12月月考数学试卷

试卷更新日期：2022-01-25 类型：月考试卷

进入出卷网下载

一、单选题

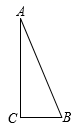
1. 若sinα＝ $\frac{1}{2}$ ，则锐角α＝（）

A、30° B、45° C、50° D、60°

查看试题解析
2. 如图，在△ABC中，∠C=90°，BC=5，AC=12，则tanB等于（）

A、 $\frac{5}{12}$ B、 $\frac{12}{5}$ C、 $\frac{5}{13}$ D、 $\frac{12}{13}$

查看试题解析
3. 在 $△$ ABC中，∠C=90°，若BC=4， $s i n A = \frac{2}{3}$ ，则AB的长为（）

A、6 B、 $2 \sqrt{5}$ C、 $3 \sqrt{5}$ D、 $2 \sqrt{13}$

查看试题解析
4. 二次函数y＝（x﹣1）²﹣3的顶点坐标是（）

A、（1，3） B、（﹣1，3） C、（1，﹣3） D、（﹣1，﹣3）

查看试题解析
5. 若将抛物线y＝x²向下平移1个单位，则所得抛物线对应的函数关系式为（）

A、y＝（x﹣1）² B、y＝（x+1）² C、y＝x²﹣1 D、y＝x²+1

查看试题解析
6. 若tanA=2，则∠A的度数估计在（）

A、在0°和30°之间 B、在30° 和45°之间 C、在45°和60°之间 D、在60°和90°之间

查看试题解析
7. 已知二次函数y=ax²+bx+c的图象如图所示，则下列结论错误的是（）

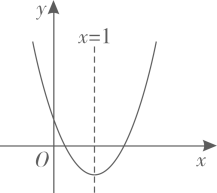A、a＞0 B、c＞0 C、b²﹣4ac＞0 D、a+b+c=0

查看试题解析
8. 如图，在 $△$ ABC中，∠C=90°，∠ABC=30°，D是AC的中点，则tan∠DBC的值是（）

A、 $\sqrt{3}$ B、 $2 \sqrt{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{3}}{6}$

查看试题解析

二、填空题

9. 计算：cos45°=.

查看试题解析
10. 若2x=5y，则 $\frac{x + y}{x} =$ .

查看试题解析
11. 抛物线 $y = 2 x^{2}$ 的图象开口向（填“上”或“下”）.

查看试题解析
12. 已知二次函数y=x²﹣kx﹣3的图象过点（1，﹣4），则k的值为 .

查看试题解析
13. 如图，点A、B、C都在格点上，则∠CAB的正切值为.

查看试题解析
14. 抛物线y=2x²+8x+m的顶点在x轴上，则m的值为.

查看试题解析
15. 在△ABC中，∠C＝90°，若tanA＝ $\frac{1}{2}$ ，则sinA＝.；

查看试题解析
16. 如图，在矩形 $A B C D$ 中， $D E ⊥ A C$ ，垂足为点 $E$ .若 $\sin ∠ A D E = \frac{4}{5}$ ， $A D = 4$ ，则 $A B$ 的长为.

查看试题解析

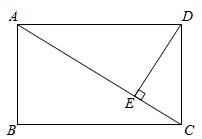
三、解答题

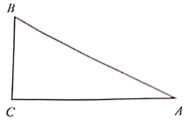
17. 如图，在Rt $△$ ABC中，∠C=90°，BC=1， $A C = \sqrt{3}$ ，求tanA与tanB的值.

查看试题解析
18. 已知二次函数y=ax²+c的图象经过点（﹣2，8）和（﹣1，5），求这个二次函数的表达式.

查看试题解析
19. 如图，已知⊙O的直径AB与弦CD互相垂直，垂足为点E.且AD=5， $c o s ∠ B C D = \frac{4}{5}$ .

(1)、求弦CD的长；

(2)、求⊙O的半径.

查看试题解析
20.
如图，小东在教学楼距地面9米高的窗口C处，测得正前方旗杆顶部A点的仰角为37°，旗杆底部B点的俯角为45°，升旗时，国旗上端悬挂在距地面2.25米处，若国旗随国歌声冉冉升起，并在国歌播放45秒结束时到达旗杆顶端，则国旗应以多少米/秒的速度匀速上升？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

查看试题解析
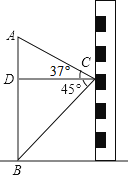21. 抛物线上部分点的横坐标、纵坐标的对应值如表：
x
﹣2
﹣1
0
0.5
1
2
3
y
0
4
6
6.25
6
4
0
请选择合适方法，求此抛物线的函数表达式.

查看试题解析
22.
如图，从热气球C上测得两建筑物A、B底部的俯角分别为30°和60度．如果这时气球的高度CD为90米．且点A、D、B在同一直线上，求建筑物A、B间的距离．

查看试题解析
23. 如图，已知抛物线y=﹣x²﹣2x+3与x轴交于点A和点B，与y轴交于点C，若点E为第二象限内抛物线上一动点，连接BE、CE.

(1)、求B、C两点的坐标；

(2)、求四边形BOCE面积的最大值.

查看试题解析
24.
如图，AB为⊙O的直径，C是⊙O上一点，过点C的直线交AB的延长线于点D，AE⊥DC，垂足为E，F是AE与⊙O的交点，AC平分∠BAE．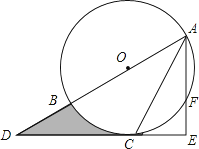

(1)、求证：DE是⊙O的切线；

(2)、若AE=6，∠D=30°，求图中阴影部分的面积．

查看试题解析
25. 如图，抛物线 $y = - x^{2} + b x + 4$ 的图象与直线l交于 $A (- 1 ， 2)$ 、 $B (3 ， n)$ 两点，点P是x轴上的一个动点，过点P作x轴的垂线交直线l于点M，交抛物线于点N，设点P的横坐标为m.

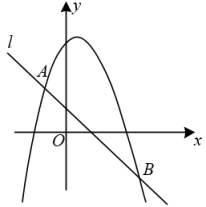(1)、b= ，n= ；

(2)、将直线AB向上平移4个单位长度，分别与x轴、y轴交于点C、D，将线段MA绕点M顺时针旋转 $90 °$ 得到线段MF.当 $\frac{1}{7} < m < 3$ 时，求 $△ A M F$ 与 $△ D B C$ 重叠部分的面积S与m的函数表达式.

查看试题解析

x	﹣2	﹣1	0	0.5	1	2	3
y	0	4	6	6.25	6	4	0