贵州省毕节市2021-2022学年九年级上学期阶段性练习三数学试卷
试卷更新日期：2022-01-25 类型：月考试卷
一、单选题
-
1. 方程的解是（ ）A、 B、 ， C、 D、 ，2. 如图，是空心圆柱体，其主视图是下列图中的（ ）
A、
B、
C、
D、
3. 某小组做“用频率估计概率”的实验时，绘出的某一结果出现的频率折线图，则符合这一结果的实验可能是（ ）
A、抛一枚硬币，出现正面朝上 B、掷一个正六面体的骰子，出现3点朝上 C、一副去掉大小王的扑克牌洗匀后，从中任抽一张牌的花色是红桃 D、从一个装有2个红球1个黑球的袋子中任取一球，取到的是黑球4. 如图，四边形ABCD和是以点O为位似中心的位似图形，若 ， 则四边形ABCD与四边形的面积比为（ ）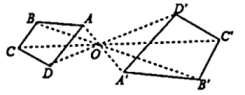
A、4：9 B、2：5 C、2：3 D、5.如图，在△ABC中，若DE∥BC，AD=5，BD=10，DE=4，则BC的值为( )
A、8 B、9 C、10 D、126. 已知中， ， ， CD是斜边AB上的中线，则的度数是（ ）
A、 B、 C、 D、7. 下列测量方案中，能确定四边形门框为矩形的是（ ）A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量对角线是否相等 D、测量对角线交点到四个顶点的距离是否都相等8. 一元二次方程 根的情况是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根9. 如图，已知矩形ABCD中，AB=3，BE=2，EF⊥BC．若四边形EFDC与四边形BEFA相似而不全等，则CE=（ ）
A、3 B、3.5 C、4 D、4.510. 如图，已知矩形ABCD沿着直线BD折叠，使点C落在C'处，BC'交AD于E，AD=8，AB=4，则DE的长为（ ）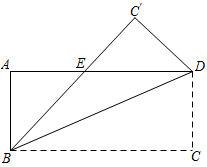
A、3 B、4 C、5 D、611. 如图，在 ABCD中，对角线AC与BD相交于点O，过点O作EF⊥AC交BC于点E，交AD于点F，连接AE、CF．则四边形AECF是（ ）
A、梯形 B、矩形 C、菱形 D、正方形12. 在图（1）、（2）所示的△ABC中，AB=4，AC=6．将△ABC分别按照图中所标注的数据进行裁剪，对于各图中剪下的两个阴影三角形而言，下列说法正确的是（ ）
A、只有（1）中的与△ABC相似 B、只有（2）中的与△ABC相似 C、都与△ABC相似 D、都与△ABC不相似13. 如图，Rt△ABC中，∠ACB=90°，斜边AB=9，D为AB的中点，F为CD上一点，且CF= CD，过点B作BE∥DC交AF的延长线于点E，则BE的长为（ ）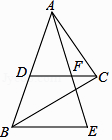
A、6 B、4 C、7 D、1214. 如图所示，在正方形ABCD中，G为CD边中点，连接AG并延长交BC边的延长线于E点，对角线BD交AG于F点．已知FG=2，则线段AE的长度为（ ）
A、6 B、8 C、10 D、1215. 如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于E，F，连接PB，PD．若AE=2，PF=8．则图中阴影部分的面积为（ ）
A、10 B、12 C、16 D、18二、填空题
-
16. 若一个菱形的两条对角线的长为3和4，则菱形的面积为.17. 已知 ，且3a－2b＋c＝9，则2a＋4b－3c＝.18. 如图，身高为1.7m的小明AB站在小河的一岸，利用树的倒影去测量河对岸一棵树CD的高度，CD在水中的倒影为C′D，A、E、C′在一条线上．如果小河BD的宽度为12m，BE=3m，那么这棵树CD的高为m．
19. 已知点C是线段AB的黄金分割点，且 ， 则AC长是.20. 如图，已知矩形OABC与矩形ODEF是位似图形，P是位似中心，若点B的坐标为 ，点E的坐标为 ，则点P的坐标为 ．
三、解答题
-
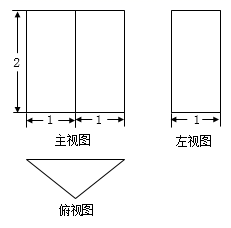
21. 如图是一个几何体的三视图，求该几何体的表面积.
22. 列方程（组）解应用题：某驻村工作队，为带动群众增收致富，巩固脱贫攻坚成效，决定在该村山脚下，围一块面积为600m2的矩形试验茶园，便于成功后大面积推广.如图所示，茶园一面靠墙，墙长35m，另外三面用69m长的篱笆围成，其中一边开有一扇1m宽的门（不包括篱笆）.求这个茶园的长和宽.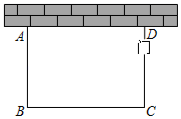
23. 某中学在艺术节期间向全校学生征集书画作品，美术王老师从全校随机抽取了四个班级记作A、B、C、D，对征集到的作品的数量进行了分析统计，制作了如下两幅不完整的统计图．
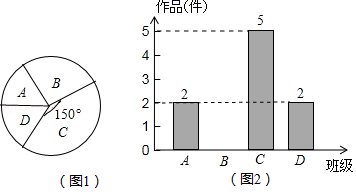(1)、王老师抽查的四个班级共征集到作品多少件？(2)、请把图2的条形统计图补充完整；(3)、若全校参展作品中有四名同学获得一等奖，其中有二名男生、二名女生．现在要在其中抽两名同学去参加学校总结表彰座谈会，请用画树状图或列表的方法求恰好抽中一名男生一名女生的概率．24. 我们知道当人的视线与物体表面互相垂直时的视觉效果最佳.如图是小亮站在距离墙壁1.60米处观察装饰画时的示意图，此时小亮的眼睛与装饰画底部A处于同一水平线上，视线恰好落在装饰画中心位置E处，且与AD垂直，已知装饰面的高度AD为0.66米.
(1)、求证：；(2)、求装饰画顶部到墙壁的距离DC（精确到0.01米）.25. 随着全球疫情的爆发，医疗物资需求猛增，某企业及时引进一条口罩生产线生产口罩，开工第一天生产口罩5000盒，第三天生产口罩7200盒，若每天增长的百分率相同．(1)、求每天增长的百分率.(2)、经调查发现，1条生产线的最大产能是15000盒/天，但是每增加1条生产线，每条生产线的产能将减少500盒/天，现该厂要保证每天生产口罩65000盒，在增加产能的同时又要节省投入的条件下（生产线越多，投入越大），应该增加几条生产线？26. 如图，点P是菱形ABCD的对角线BD上一点，连接CP并延长，交AD于E，交BA的延长线于点F.
(1)、求证： ；(2)、如果 ， ， 求线段PA的长.27.
(1)、问题：如图1，在四边形ABCD中，点P为AB上一点，∠DPC=∠A=∠B=90°.求证：AD·BC=AP·BP.(2)、探究：如图2，在四边形ABCD中，点P为AB上一点，当∠DPC=∠A=∠B=θ时，上述结论是否依然成立.说明理由.(3)、应用：请利用（1）（2）获得的经验解决问题：如图3，在△ABD中，AB=6，AD=BD=5.点P以每秒1个单位长度的速度，由点A 出发，沿边AB向点B运动，且满足∠DPC=∠A.设点P的运动时间为t（秒），当DC的长与△ABD底边上的高相等时，求t的值.