甘肃省酒泉市肃州区第六片区2021-2022学年八年级上学期期末考试数学试卷
试卷更新日期:2022-01-25 类型:期末考试
一、单选题
-
1. 下列各数中为无理数的是( )A、 B、 C、 D、2. 点P的坐标为(﹣3,2),则点P位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 4 的算术平方根是A、 16 B、2 C、-2 D、4. 四根小棒的长分别是5,9,12,13,从中选择三根小棒首尾相接,搭成边长如下的四个三角形,其中是直角三角形的是( )A、5,9,12 B、5,9,13 C、5,12,13 D、9,12,135. 估计 的值在( )A、和 之间 B、和 之间 C、和 之间 D、和 之间6. 直角坐标系中,点在一次函数的图象上,则的值是( )A、 B、 C、 D、7. 如下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲
乙
丙
丁
平均数(cm)
185
180
185
180
方差
2.5
2.5
6.4
7.1
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A、甲 B、乙 C、丙 D、丁8. 如图,是的角平分线, , 交于点.已知 , 则的度数为( ) A、 B、 C、 D、9. 正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )A、
A、 B、 C、 D、9. 正比例函数y=kx(k≠0)的图象在第二、四象限,则一次函数y=x+k的图象大致是( )A、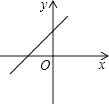 B、
B、 C、
C、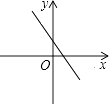 D、
D、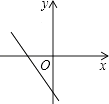 10. 《九章算术》中记载:“今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?”意思是:现有一些人共同买一个物品,每人出8元,还余3元;每人出7元,还差4元.问共有多少人?这个物品价格是多少元?设共有 个人,这个物品价格是 元.则可列方程组为( )A、 B、 C、 D、
10. 《九章算术》中记载:“今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?”意思是:现有一些人共同买一个物品,每人出8元,还余3元;每人出7元,还差4元.问共有多少人?这个物品价格是多少元?设共有 个人,这个物品价格是 元.则可列方程组为( )A、 B、 C、 D、二、填空题
-
11. 比较大小: 1.(选填“<”“>”或“=”)12. 线段AB=5,AB平行于x轴,A在B左边,若A点坐标为(-1,3),则B点坐标为.13. 已知是关于的二元一次方程的一个解,则的值为.14. 如图,在△ABC中,点D在CB的延长线上,∠A=60°,∠ABD=110°,则∠C等于.
 15. 如图,已知 和 的图象交于点P,根据图象可得关于X、Y的二元一次方程组 的解是 .
15. 如图,已知 和 的图象交于点P,根据图象可得关于X、Y的二元一次方程组 的解是 . 16. 八年级(1)、(2)两班人数相同,在同一次数学单元测试中,班级平均分和方差如下:则成绩较为稳定的班级是.
16. 八年级(1)、(2)两班人数相同,在同一次数学单元测试中,班级平均分和方差如下:则成绩较为稳定的班级是.
17. 如图是一个三级台阶,它的每一级的长、宽、高分别为 , 和 , 和 是这个台阶的两个端点, 点上有一只蚂蚁想到 点去吃可口的食物,则它所走的最短路线长度为 . 18. 在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
18. 在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换:
f(m,n)=(m,-n),如f(2,1)=(2,-1);
g(m,n)=(-m,-n),如g(2,1)=(-2,-1).
按照以上变换有:f[g(3,4)]=f(-3,-4)=(-3,4),那么g[f(2,-3)]=.三、解答题
-
19. 化简:(1)、(2)、20. 解方程组:(1)、(2)、21. 5年前母亲的年龄是女儿年龄的15倍,15年后,母亲的年龄比女儿年龄的2倍多6岁.那么现在这对母女的年龄分别是多少?22. 已知:如图, , 点E在AC上.求证: .
 23. 随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9(1)、这组数据的中位数是 , 众数是;(2)、计算这10位居民一周内使用共享单车的平均次数;(3)、若该小区有2000位居民,试估计该小区居民一周内使用共享单车的总次数.
23. 随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9(1)、这组数据的中位数是 , 众数是;(2)、计算这10位居民一周内使用共享单车的平均次数;(3)、若该小区有2000位居民,试估计该小区居民一周内使用共享单车的总次数.