四川省南充市2021-2022学年七年级上学期期末数学试卷
试卷更新日期:2022-01-25 类型:期末考试
一、单选题
-
1. 下列有理数中,最小的是( )A、 B、0 C、 D、2. 嘉陵江是长江的第二大支流,流经甘肃、陕西、四川、重庆四省市,全长 , 流域面积约是 . 把160000用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图,点O在直线上, , 则的大小为( )
 A、 B、 C、 D、5. 下列表述不正确的是( )A、葡萄的单价是4元/ , 表示葡萄的金额 B、正方形的边长为表示这个正方形的周长 C、某校七年级有4个班,平均每个班有a名男生,表示全校七年级男生总数 D、一个两位数的十位和个位数字分别为4和表示这个两位数6. 下列4个平面图形中,能够围成圆柱侧面的是( )A、
A、 B、 C、 D、5. 下列表述不正确的是( )A、葡萄的单价是4元/ , 表示葡萄的金额 B、正方形的边长为表示这个正方形的周长 C、某校七年级有4个班,平均每个班有a名男生,表示全校七年级男生总数 D、一个两位数的十位和个位数字分别为4和表示这个两位数6. 下列4个平面图形中,能够围成圆柱侧面的是( )A、 B、
B、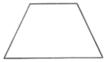 C、
C、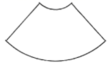 D、
D、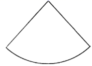 7. 小明家的汽车在阳光下曝晒后车内温度达到了60℃,打开车门后经过降低到室外同温32℃,再启动空调关车门,若每分钟降低4℃,降到设定的20℃共用时间是( )A、 B、 C、 D、8. 下列说法中,正确的是( )A、射线和射线是同一条射线 B、若 , 则点B为线段的中点 C、点在一条直线上,则 D、点C在线段上,分别是线段的中点,则9. 商店元旦促销,某款衣服打8折销售.每件比标价少35元,仍获利15元.下列说法:①衣服标价为每件175元;②衣服促销单价为140元;③衣服的进价为每件125元;④不打折时商店的利润为每件50元.正确的共有( )A、4个 B、3个 C、2个 D、1个10. 已知a为自然数,关于x的一元一次方程的解也是自然数,则满足条件的自然数a共有( )A、3个 B、4个 C、5个 D、6个
7. 小明家的汽车在阳光下曝晒后车内温度达到了60℃,打开车门后经过降低到室外同温32℃,再启动空调关车门,若每分钟降低4℃,降到设定的20℃共用时间是( )A、 B、 C、 D、8. 下列说法中,正确的是( )A、射线和射线是同一条射线 B、若 , 则点B为线段的中点 C、点在一条直线上,则 D、点C在线段上,分别是线段的中点,则9. 商店元旦促销,某款衣服打8折销售.每件比标价少35元,仍获利15元.下列说法:①衣服标价为每件175元;②衣服促销单价为140元;③衣服的进价为每件125元;④不打折时商店的利润为每件50元.正确的共有( )A、4个 B、3个 C、2个 D、1个10. 已知a为自然数,关于x的一元一次方程的解也是自然数,则满足条件的自然数a共有( )A、3个 B、4个 C、5个 D、6个二、填空题
-
11. 计算: .12. 钟面上7点30分时,时针与分针的夹角的度数是 .13. 加上等于的多项式是 .14. 若 , 则等于 .15. 中国古代数学著作《孙子算经》中有个问题:今有三人共车,二车空;二人共车,九人步,问人与车各几何?这道题的意思是:今有若干人乘车,每三人乘一车,最终剩余2辆车,若每2人共乘一车,最终剩余9个人无车可乘,问有多少人,多少辆车?如果我们设有x辆车,则可列方程 .16. 如图,数轴上两点对应的数分别为 , 若数轴上的点C满足 , 则点C表示的数为 .
三、解答题
-
17. 计算:(1)、;(2)、 .18. 先化简,再求值: , 其中 .19. 某检修小组乘一辆汽车在东西走向的公路上检修线路,约定向东行为正,某天从A地出发到收工时的行动记录如下(单位:):
次数
1
2
3
4
5
6
7
8
9
记录
(1)、问收工时检修小组是否回到A地;如果没有回到A地,请说明检修小组最后的位置.(2)、距离A地最近的记录是哪一次?距离多远?20.(1)、解方程: .(2)、若方程 和关于x的方程 的解相同,试求a的值.21. 如图,已知四点 .
(1)作图:连接 , 在的延长线上取点E,使 .
(2)作图:在直线上找一点P,使它到点A,点B的距离之和最小.
(3)用适当的语句表述作出图中的点与线的关系.(作图不用写作法,(3)问要求写其中4句即可.)22. 如图,在桌上放置一副三角板(忽略厚度),直角与角顶点重合.三角板可绕着点A旋转. (1)、当平分时,求的度数.(2)、在旋转过程中,保持在内部,求的度数.23. 如图,甲、乙两块长方形苗圃的长与宽相同,分别为 , 中间都有两条横、竖交错的通道.甲苗圃横、竖通道的宽分别为 , 乙苗圃横、竖通道的宽分别为 .
(1)、当平分时,求的度数.(2)、在旋转过程中,保持在内部,求的度数.23. 如图,甲、乙两块长方形苗圃的长与宽相同,分别为 , 中间都有两条横、竖交错的通道.甲苗圃横、竖通道的宽分别为 , 乙苗圃横、竖通道的宽分别为 . (1)、用含x的式子表示两苗圃通道的面积 .(2)、比较的大小,并求两者之差.24. 为发展校园足球运动,某校决定购买一批足球运动装备.甲、乙两商场销售同种品牌的足球和足球队服,标价一致,每个足球比每套队服少50元,两套队服与3个足球的费用相等.经洽谈,甲商场优惠方案是:每购买10套队服,送1个足球.乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)、每个足球和每套队服的价格是多少元?(2)、若购买100套队服和个足球,请用含a的式子分别表示到甲商场和乙商场所花的费用.(3)、初中年级到甲商场购买100套队服和若干箱足球(每箱10个),高中年级在乙商场购买相同装备,付费相同,求学校共买足球箱数.25. 如图,O为原点,长方形与的面积都为12,且能够完全重合,边在数轴上, . 长方形可以沿数轴水平移动,移动后的长方形与重叠部分的面积记为S.
(1)、用含x的式子表示两苗圃通道的面积 .(2)、比较的大小,并求两者之差.24. 为发展校园足球运动,某校决定购买一批足球运动装备.甲、乙两商场销售同种品牌的足球和足球队服,标价一致,每个足球比每套队服少50元,两套队服与3个足球的费用相等.经洽谈,甲商场优惠方案是:每购买10套队服,送1个足球.乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)、每个足球和每套队服的价格是多少元?(2)、若购买100套队服和个足球,请用含a的式子分别表示到甲商场和乙商场所花的费用.(3)、初中年级到甲商场购买100套队服和若干箱足球(每箱10个),高中年级在乙商场购买相同装备,付费相同,求学校共买足球箱数.25. 如图,O为原点,长方形与的面积都为12,且能够完全重合,边在数轴上, . 长方形可以沿数轴水平移动,移动后的长方形与重叠部分的面积记为S. (1)、如图1,求出数轴上点F表示的数.(2)、当S恰好等于长方形面积的一半时,求出数轴上点表示的数.(3)、在移动过程中,设P为线段的中点,点所表示的数能否互为相反数?若能,求点O移动的距离;若不能,请说明理由.
(1)、如图1,求出数轴上点F表示的数.(2)、当S恰好等于长方形面积的一半时,求出数轴上点表示的数.(3)、在移动过程中,设P为线段的中点,点所表示的数能否互为相反数?若能,求点O移动的距离;若不能,请说明理由.