四川省眉山市仁寿县2020-2021学年七年级上学期期末数学试卷
试卷更新日期:2022-01-25 类型:期末考试
一、单选题
-
1. 的绝对值是( )A、 B、2021 C、 D、2. 在1, , , 0这四个有理数中,最小的数是( )A、 B、0 C、 D、13. 下列四个数中,数值不同于其他三个的是( )A、 B、 C、 D、4. 下面说法正确的是( )A、倒数等于它本身的数是1 B、是最大的负整数 C、单项式的系数是 , 次数是2 D、与是同类项5. 如图是几何体的俯视图,所表示数字为该位置小正方体的个数,则该几何体的正视图是( )
 A、
A、 B、
B、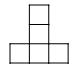 C、
C、 D、
D、 6.
6.
嫦娥五号”在距地球约384400千米之外完成了中国航天史上“最复杂的任务”,中国成为了人类第三个获取月球样本的国家.将近似数384400精确到万位,并用科学记数法表示为( )A、 B、 C、 D、7. 点A表示数轴上的一个点,将点A向右移动6个单位,再向左移动4个单位,终点恰好是原点,则点A表示的数是( )A、 B、 C、0 D、8. 按如图所示的程序运算:当输入的数据为1时,则输出的数据是( )
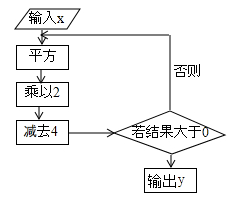 A、2 B、4 C、6 D、89. 在灯塔P处观测到轮船A位于北偏西55°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( )
A、2 B、4 C、6 D、89. 在灯塔P处观测到轮船A位于北偏西55°的方向,同时轮船B在南偏东15°的方向,那么∠AOB的大小为( ) A、100° B、105° C、125° D、140°10. 已知 , , 且 , 则的值是( )A、或 B、 C、 D、或811. 当时,代数式的值为2,则当时,代数式的值为( )A、 B、 C、2 D、612. 如图,已知直线AB∥CD,直线EF分别与AB、CD交于点M、N,点H在直线CD上,HG⊥EF于点G,过点G作GP∥AB.则下列结论:①∠AMF与∠DNF是对顶角;②∠PGM=∠DNF;③∠BMN+∠GHN=90°;④∠AMG+∠CHG=270°.其中正确结论的个数( )
A、100° B、105° C、125° D、140°10. 已知 , , 且 , 则的值是( )A、或 B、 C、 D、或811. 当时,代数式的值为2,则当时,代数式的值为( )A、 B、 C、2 D、612. 如图,已知直线AB∥CD,直线EF分别与AB、CD交于点M、N,点H在直线CD上,HG⊥EF于点G,过点G作GP∥AB.则下列结论:①∠AMF与∠DNF是对顶角;②∠PGM=∠DNF;③∠BMN+∠GHN=90°;④∠AMG+∠CHG=270°.其中正确结论的个数( )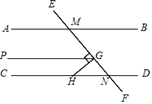 A、1个 B、2 个 C、3个 D、4个
A、1个 B、2 个 C、3个 D、4个二、填空题
-
13. 如果“”表示增产 , 那么“”表示.14. 已知 , 则 , .15. 定义一种新运算⊗:x⊗y=3x﹣2y,那么(﹣5)⊗4=.16. 如图是一个正方体纸盒的展开图,正方体的各面标有数1,2,3, , 相对面上的两个数互为相反数,则.
 17. 已知a,b两数在数轴上对应的点如图所示,化简的结果是.
17. 已知a,b两数在数轴上对应的点如图所示,化简的结果是. 18. 一根绳子弯曲成如图1所示的形状.当用剪刀像图2那样沿虚线a把绳子剪断时,绳子被剪为5段;当用剪刀像图3那样沿虚线b(b∥a)把绳子再剪一次时,绳子就被剪为9段.若用剪刀在虚线a,b之间把绳子再剪(n﹣2)次(剪刀的方向与a平行),这样一共剪n次时绳子的段数是.
18. 一根绳子弯曲成如图1所示的形状.当用剪刀像图2那样沿虚线a把绳子剪断时,绳子被剪为5段;当用剪刀像图3那样沿虚线b(b∥a)把绳子再剪一次时,绳子就被剪为9段.若用剪刀在虚线a,b之间把绳子再剪(n﹣2)次(剪刀的方向与a平行),这样一共剪n次时绳子的段数是.
三、解答题
-
19. 计算:.20. 化简:.21. 阅读并完成下列推理过程,在括号内填写理由.
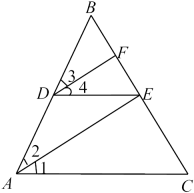
已知:如图,点D,E分别在线段 、 上, , 平分 , 平分 交 于点E、F.
求证: .
证明: 平分 (已知),
.
平分 (已知),
_▲_(角平分线的定义),
(已知),
.
.
.
22. 若 , , 且a、b互为倒数,求 的值.23. 如图,已知线段AB上有两点C、D,且AC:CD:DB=2:3:4,E,F分别为AC、DB的中点,EF=12cm.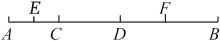 (1)、线段BC的长;(2)、线段AB的长;(3)、若点G在直线AB上,且GB=3cm,求线段DG的长.24. 2020年12月8日,中尼两国共同宣布珠穆朗玛峰的最新测定高度为8848.86米.今有某登山队5名队员在一次登山活动中,以二号高地为基地,开始向海拔距二号高地500米的顶峰冲刺,设他们向上走为正,行程单位:记录如下: , , , , , , , .(1)、他们最终有没有登上顶峰?如果没有,那么他们离顶峰还差多少米?(2)、登山时,5名队员在登山全程中都使用了氧气瓶,且每人向下行走每米要消耗氧气m升,向上行走每米还要多消耗0.01升,求他们共消耗了氧气多少升?(用含m的代数式表示)
(1)、线段BC的长;(2)、线段AB的长;(3)、若点G在直线AB上,且GB=3cm,求线段DG的长.24. 2020年12月8日,中尼两国共同宣布珠穆朗玛峰的最新测定高度为8848.86米.今有某登山队5名队员在一次登山活动中,以二号高地为基地,开始向海拔距二号高地500米的顶峰冲刺,设他们向上走为正,行程单位:记录如下: , , , , , , , .(1)、他们最终有没有登上顶峰?如果没有,那么他们离顶峰还差多少米?(2)、登山时,5名队员在登山全程中都使用了氧气瓶,且每人向下行走每米要消耗氧气m升,向上行走每米还要多消耗0.01升,求他们共消耗了氧气多少升?(用含m的代数式表示)