河南省南阳市镇平县2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-01-25 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\sqrt{3} ＜ a ＜ \sqrt{17}$ ，则整数a的值不可能为（）

A、2 B、3 C、4 D、5

查看试题解析
2. 同时掷两枚质地均匀的正方体骰子，骰子的六个面上分别刻有1到6的点数，下列事件中是不可能发生的事件是( )

A、点数之和为12 B、点数之和小于3 C、点数之和大于4且小于8 D、点数之和为13

查看试题解析
3. 已知一元二次方程x²＋k﹣3＝0有一个根为1，则k的值为（）

A、﹣2 B、2 C、﹣4 D、4

查看试题解析
4. 根据下列表格的对应值，判断方程ax²+bx+c=0（a≠0，a、b、c为常数）一个解的范围是（　　）
x
3.23
3.24
3.25
3.26
ax²+bx+c
﹣0.06
﹣0.02
0.03
0.09

A、3＜x＜3.23 B、3.23＜x＜3.24 C、3.24＜x＜3.25 D、3.25＜x＜3.26

查看试题解析
5. 如图，电线杆 $C D$ 的高度为h，两根拉线 $A C$ 与 $B C$ 相互垂直， $∠ C A B = θ$ ，则拉线 $B C$ 的长度为（A、D、B在同一条直线上）（）

A、 $\frac{h}{s i n θ}$ B、 $\frac{h}{c o s θ}$ C、 $\frac{h}{t a n θ}$ D、 $h ⋅ c o s θ$

查看试题解析
6. 某中学组织九年级学生篮球比赛，以班为单位，每两班之间都比赛一场，总共安排15场比赛，则共有多少个班级参赛（）

A、6 B、5 C、4 D、3

查看试题解析
7. 如图，在△ABC中，点D、E分别是AB、AC的中点，若△ABC的面积为16，则四边形BCED的面积为（）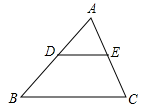

A、8 B、12 C、14 D、16

查看试题解析
8. 如图1所示，△DEF中，∠DEF＝90°，∠D＝30°，B是斜边DF上一动点，过B作AB⊥DF于B，交边DE（或边EF）于点A，设BD＝x，△ABD的面积为y，图2是y与x之间函数的图象，则△ABD面积的最大值为（）

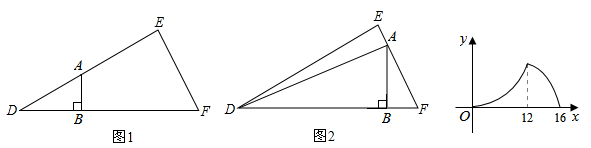A、8 $\sqrt{3}$ B、16 $\sqrt{3}$ C、24 $\sqrt{3}$ D、48 $\sqrt{3}$

查看试题解析
9. 小轩从如图所示的二次函数y＝ax²＋bx＋c（a≠0）的图象中，观察得出了下面五条信息：①abc＜0；②a＋b＋c＜0；③4ac﹣b²＞0；④a $＝ \frac{3}{2}$ b；⑤b＋2c＞0.你认为其中正确信息的个数有（）

A、2 B、3 C、4 D、5

查看试题解析
10.
如图，平行四边形OABC的顶点O（0，0），A（1，2），点C在x轴的正半轴上，延长BA交y轴于点D.将△ODA绕点O顺时针旋转得到△OD'A'，当点D的对应点D'落在OA上时，D'A'的延长线恰好经过点C，则点B的坐标为（）

A、（2 $\sqrt{5}$ ， 2） B、（2 $\sqrt{3}$ ， 2） C、（2 $\sqrt{3} ＋$ 1，2） D、（2 $\sqrt{5} ＋$ 1，2）

查看试题解析

二、填空题

11. 计算 $\sqrt{12}$ ﹣9 $\sqrt{\frac{1}{3}}$ 的结果是．

查看试题解析
12. 关于x的一元二次方程x²+2x+m=0有两个相等的实数根，则m的值是．

查看试题解析
13. 若抛物线y＝x²＋ax＋b与x轴两个交点间的距离为2，对称轴为直线x＝1，则抛物线的解析式为.

查看试题解析
14. 某学校举行中华传统文化知识大赛活动，从三名男生和两名女生中选出两名同学担任本次活动的主持人，则选出的恰为一男一女的概率是．

查看试题解析
15. 如图，在等边三角形ABC中，AB＝2 $\sqrt{3}$ ，点M为边BC的中点，点N为边AB上的任意一点（不与点A，B重合），将△BMN沿直线MN折叠，若点B的对应点B'恰好落在等边三角形ABC的边上，则BN的长为.

查看试题解析

三、解答题

16. 先化简，再求值：（1 $- \frac{5}{x ＋ 2} ） \div \frac{x^{2} - 6 x ＋ 9}{x ＋ 2}$ ，其中x＝3 $- \sqrt{3}$ .

查看试题解析
17. 已知关于x的一元二次方程x²+2（m﹣1）x+m²﹣3＝0有两个不相等的实数根．

(1)、求m的取值范围；

(2)、若m为非负整数，且该方程的根都是无理数，求m的值．

查看试题解析
18. 如图，在等边三角形ABC中，点D，E分别在BC，AB上，且∠ADE＝60°.求证：△ADC∽△DEB.

查看试题解析
19. 在一个不透明的袋中装有5个只有颜色不同的球，其中3个黄球，2个黑球.

(1)、用画树状图或列表的方法求从袋中同时摸出的两个球都是黄球的概率；

(2)、再往袋中放入若干个黑球，搅匀后，若从袋中摸出一个球是黑球的概率是 $\frac{2}{3}$ ，求放入袋中的黑球的个数.

查看试题解析
20. 二次函数y＝ax²＋bx＋c的图象经过点A（4，0），B（0，﹣3），C（﹣2，0），求它的解析式，直接写出它的开口方向、对称轴和顶点坐标.

查看试题解析
21. 如图，某风景区内有一瀑布，AB表示瀑布的垂直高度，在与瀑布底端同一水平位置的点D处测得瀑布顶端A的仰角 $β$ 为45°，斜坡CD的坡度i＝3∶4，CD＝100米，在观景台C处测得瀑布顶端A的仰角 $α$ 为37°，若点B、D、E在同一水平线上，求瀑布的落差AB.（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

查看试题解析
22. 如图1，在△ABC中，AB＝AC＝2，∠BAC＝120°，点D、E分别是AC、BC的中点，连接DE.

(1)、探索发现：
图1中， $\frac{A B}{B C}$ 的值为， $\frac{A D}{B E}$ 的值为.

(2)、拓展探究
若将△CDE绕点C旋转，在旋转过程中 $\frac{A D}{B E}$ 的大小有无变化？请仅就图2的情形给出证明.

(3)、问题解决
当△CDE旋转至A，D，C三点共线时，直接写出线段BE的长.

查看试题解析
23. 如图，在平面直角坐标系中，二次函数y＝﹣x²＋bx＋c的图象与坐标轴交于A，B，C三点，其中点B的坐标为（1，0），点C的坐标为（0，4），点D的坐标为（0，2），点P为二次函数图象上的动点.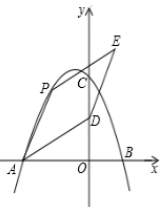

(1)、求二次函数的解析式和直线AD的解析式；

(2)、当点P位于第二象限内二次函数的图象上时，连接AD，AP，以AD，AP为邻边作平行四边形APED，设平行四边形APED的面积为S，求S的最大值.

查看试题解析

x	3.23	3.24	3.25	3.26
ax²+bx+c	﹣0.06	﹣0.02	0.03	0.09