浙江省温州市瓯海区三校联考2021-2022学年八年级上学期12月月考数学试卷

试卷更新日期：2022-01-25 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列“祝你成功”的首拼字母中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 根据下列表述，能够确定具体位置的是（）

A、北偏东25°方向 B、距学校800米处 C、温州大剧院音乐厅8排 D、东经20°北纬30°

查看试题解析
3. 在△ABC中，若AB＝3，BC＝4，且周长为奇数，则第三边AC的长可以是（）

A、1 B、3 C、4 D、5

查看试题解析
4. 如果 a＞b，那么下列各式中正确的是（）

A、a＋1＜b＋1 B、－a＋3＜－b＋3 C、－a＞－b D、 $\frac{a}{2} < \frac{b}{2}$

查看试题解析
5. 已知点A（a+9，2a+6）在y轴上，a的值为（）

A、﹣9 B、9 C、3 D、﹣3

查看试题解析
6. 如图，△ABC中，D，E分别为BC，AD的中点，若△CDE的面积使2，则△ABC的面积是（）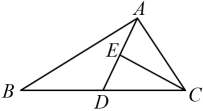

A、4 B、5 C、6 D、8

查看试题解析
7. 某校在一次外出郊游中，把学生编为9个组，若每组比预定的人数多1人，则学生总数超过200人；若每组比预定的人数少1人，则学生总数不到190人，那么每组预定的学生人数为（）

A、24人 B、23人 C、22人 D、不能确定

查看试题解析
8. 在平面直角坐标系中，已知点A（3，﹣3），在坐标轴上确定一点B，使△AOB为等腰三角形，则符合条件的点B共有（）个

A、5 B、6 C、7 D、8

查看试题解析
9. 如图，在△ABC的右侧以AC为边构造等腰Rt△ACD，其中∠CAD为90°，在BC的延长线上取一点E，使∠ADE＝∠ACB.若DE＝BC，且四边形ACED的面积为8，则AB的长为（）

A、2 B、4 C、 $\sqrt{8}$ D、8

查看试题解析
10. 对于坐标平面内的点，先将该点向右平移1个单位，再向上平移2个单位，这种点的运动称为点的斜平移，如点P（2，3）经1次斜平移后的点的坐标为（3，5）.已知点A的坐标为（2，0），点Q是直线l上的一点，点A关于点Q的对称点为点B，点B关于直线l的对称点为点C，若点B由点A经n次斜平移后得到，且点C的坐标为（8，6），则△ABC的面积是（）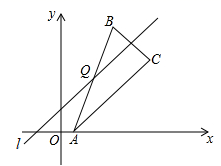

A、12 B、14 C、16 D、18

查看试题解析

二、填空题

11. 根据“3x与5的和是负数”可列出不等式 .

查看试题解析
12. 命题“a＜2a”是命题（填“真”或“假”）.

查看试题解析
13. 在平面直角坐标系中，点P（2，﹣3）到x轴的距离为 .

查看试题解析
14. 如图，在△ABC中，∠ACB=90°，D在BC上，E是AB的中点，AD、CE相交于F，且AD=DB．若∠B=20°，则∠DFE等于．

查看试题解析
15. 如图，等腰△ABC中，AB＝AC＝5，BC＝6，BD⊥AC，则BD＝.

查看试题解析
16. 不等式组 ${\begin{array}{l} x - a \geq 0 \\ 1 - 2 x > - 3 \end{array}$ 的整数解共有4个，则a的取值范围是 .

查看试题解析
17. 如图，在长方形ABCD中，AB=2，BC=4，点E在边AD上，连接BE，将△EAB沿BE翻折得到△EA′B，延长EA′交BC于点F，若四边形EFCD的周长为9，则AE的长为

查看试题解析
18. 如图，在Rt△ABC中，∠ACB=90°，∠ABC=60°，AB=4，点D是BC上一动点，以BD为边在BC的右侧作等边△BDE，F是DE的中点，连结AF，CF，则AF+CF的最小值是.

查看试题解析

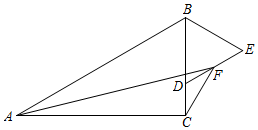
三、解答题

19. 解不等式组 ${\begin{array}{l} 3 (x + 1) \geq x - 1 \\ \frac{x + 9}{2} > 2 x \end{array}$ ，并把解集表示在数轴上.

查看试题解析
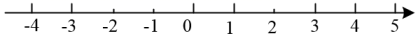20. 如图，已知点B、F、C、E在同一直线上，AB∥DE，AB＝DE，BF＝CE.求证：AC∥DF.

查看试题解析
21. 在直角坐标系中，我们把横、纵坐标都为整数的点称为整点，记顶点都是整点的三角形为整点三角形，如图，已知整点A（2，2），B（4，1），请在所给网格区域（含边界）上按要求画整点三角形.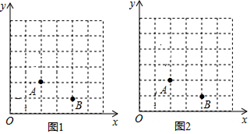

(1)、在图1中画一个等腰△PAB，使点P的横坐标大于点A的横坐标.

(2)、在图2中画一个直角△PAB，使点P的横坐标等于点P，B的纵坐标之和.

查看试题解析
22. 如图，已知点P是等边△ABC内一点，连结PA，PB，PC，D为△ABC外一点，且∠DAC＝∠PAB，AD＝AP，连结DP，DC.

(1)、求证：△ADC≌△APB.

(2)、若PA＝4，PB＝3，PC＝5，求∠APB的度数.

查看试题解析
23. 某商场销售A，B两种品牌的教学设备，这两种教学设备的进价和售价如表所示

A
B
进价（万元/套）
1.5
1.2
售价（万元/套）
1.65
1.4
该商场计划购进两种教学设备若干套，共需66万元，全部销售后可获毛利润9万元．

(1)、该商场计划购进A，B两种品牌的教学设备各多少套？

(2)、通过市场调研，该商场决定在原计划的基础上，减少A种设备的购进数量，增加B种设备的购进数量，已知B种设备增加的数量是A种设备减少的数量的1.5倍．若用于购进这两种教学设备的总资金不超过69万元，问A种设备购进数量至多减少多少套？

查看试题解析
24. 如图，在平面直角坐标系中，已知点 $A (0 ， a)$ ，点 $B (b ， 0)$ ，其中a，b满足 $| 4 - a | + (b - 3)^{2} = 0$ ，点P从点O出发，沿 $O \to B \to A$ 的路径以每秒2个单位的速度向终点A运动，设运动时间为t秒.

(1)、求线段 $A B$ 的值.

(2)、是否存在t，使得 $△ O B P$ 为等腰三角形，若存在，请求出所有t的值，若不存在，请说明理由.

(3)、当 $A P$ 平分 $∠ O A B$ 时，求t的值.

(4)、线段 $A B$ 绕点A按逆时针方向旋转90得到线段 $A C$ ，连结 $B C$ ，若该平面内存在点 $Q (3 ， m)$ ，使得 $△ A B Q$ 与 $△ A B C$ 的面积相等，则m的值为.

查看试题解析

	A	B
进价（万元/套）	1.5	1.2
售价（万元/套）	1.65	1.4