贵州省毕节市2021-2022学年八年级上学期阶段性练习三数学试卷
试卷更新日期:2022-01-25 类型:月考试卷
一、单选题
-
1. 以下列各组线段为边作三角形,能构成直角三角形的是( )A、2,3,5 B、6,8,9 C、5,12,13 D、6,12,132. 64的立方根是( )A、4 B、±4 C、8 D、±83. 若 , 那么( )A、1 B、-1 C、-3 D、-54. 根据下列表述,能确定位置的是( )A、光明剧院8排 B、毕节市麻园路 C、北偏东40° D、东经116.16°,北纬36.39°5. 计算: ( )A、 B、 C、 D、6. 梯子的底端离建筑物6米,10米长的梯子可以到达建筑物的高度是( )A、6米 B、7米 C、8米 D、9米7. 在平面直角坐标系中,点在( )A、轴正半轴上 B、轴负半轴上 C、轴正半轴上 D、轴负半轴上8. 下列函数中,是一次函数的是( )A、 B、 C、 D、9. 下列计算正确的是( )A、=2 B、= C、=x D、10. 下列说法中正确的是( )A、已知a,b,c是三角形的三边,则a2+b2=c2 B、在直角三角形中两边和的平方等于第三边的平方 C、在Rt△ABC中,∠C=90°,所以a2+b2=c2 D、在Rt△ABC中,∠B=90°,所以a2+b2=c211. 若式子有意义,则实数m的取值范围是( )A、且 B、且 C、 D、12. 一次函数的图象大致是( )A、
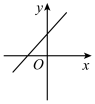 B、
B、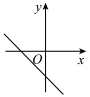 C、
C、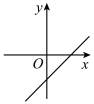 D、
D、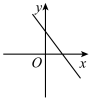 13. 如图,阴影部分是一个长方形,它的面积是( )
13. 如图,阴影部分是一个长方形,它的面积是( ) A、3cm2 B、4cm2 C、5cm2 D、6cm214. 已知直角三角形的斜边长为5cm,周长为12cm,则这个三角形的面积( )A、 B、 C、 D、15. 实数a、b在数轴上的位置如图所示化简,的结果为( )
A、3cm2 B、4cm2 C、5cm2 D、6cm214. 已知直角三角形的斜边长为5cm,周长为12cm,则这个三角形的面积( )A、 B、 C、 D、15. 实数a、b在数轴上的位置如图所示化简,的结果为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
16. 在△ABC中,若AC2+BC2=AB2 , ∠A∶∠B=1∶2,则∠B的度数是.17. 方程的解是.18. 在函数的图象上有 , , 三个点,则 , , 的大小关系是.(用“>”连接)19. 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD= , 则BC=.
 20. 记的整数部分是 , 小数部分是 , 则的值为.
20. 记的整数部分是 , 小数部分是 , 则的值为.三、解答题
-
21. 计算:(1)、;(2)、.22. 先化简,再求值: , 其中.23. 已知.(1)、求的值;(2)、求的平方根.24. 如图,是某种蜡烛在燃烧过程中高度与时间之间关系的图象,由图象解答下列问题:
 (1)、此蜡烛燃烧1小时后,高度为cm;经过小时燃烧完毕;(2)、求这个蜡烛在燃烧过程中高度与时间之间关系的解析式.
(1)、此蜡烛燃烧1小时后,高度为cm;经过小时燃烧完毕;(2)、求这个蜡烛在燃烧过程中高度与时间之间关系的解析式.
