黑龙江省大庆市龙凤区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列具有二次函数关系的是（）

A、正方形的周长y与边长x B、速度一定时，路程s与时间t C、三角形的高一定时，面积y与底边长x D、正方形的面积y与边长x

查看试题解析
2. 如图，在Rt△ABC中，∠ACB＝90°， $\frac{B C}{A C} = \frac{1}{2}$ ，则下列结论中正确的是（）

A、 $\sin A = \frac{1}{2}$ B、sinB＝ $\frac{\sqrt{5}}{5}$ C、cosA＝ $\frac{\sqrt{5}}{5}$ D、tanB＝2

查看试题解析
3. 如图， $A D$ 是 $⊙ O$ 的直径， $\overset{⌢}{A B} = \overset{⌢}{C D}$ ，若 $∠ A O B = 40 °$ ，则圆周角 $∠ B P C$ 的度数是（）

A、 $40 °$ B、 $50 °$ C、 $60 °$ D、 $70 °$

查看试题解析
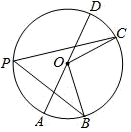4. 小明不慎把家里的圆形玻璃打碎了，其中四块碎片如图所示，为配到与原来大小一样的圆形玻璃，小明带到商店去的一块玻璃碎片应该是（　　）

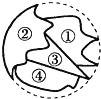A、第①块 B、第②块 C、第③块 D、第④块

查看试题解析
5.
如图，半径为3的⊙A经过原点O和点C（0，2），B是y轴左侧⊙A优弧上一点，则tan∠OBC为（　　）

A、 $\frac{1}{3}$ B、2 $\sqrt{2}$ C、 $\frac{\sqrt{2}}{4}$ D、 $\frac{2 \sqrt{2}}{3}$

查看试题解析
6. 如图，△ABC的内切圆⊙O与AB ， BC ， CA分别相切于点D ， E ， F ，且AD＝2，BC＝5，则△ABC的周长为（）

A、16 B、14 C、12 D、10

查看试题解析
7. 如图，直角坐标系中，以5为半径的动圆的圆心A沿x轴移动，当⊙ $A$ 与直线 $l ： y = \frac{5}{12} x$ 只有一个公共点时，点A的坐标为（）

A、 $(- 12 ， 0)$ B、 $(- 13 ， 0)$ C、 $(\pm 12 ， 0)$ D、 $(\pm 13 ， 0)$

查看试题解析
8. 如图，在△ABC中点D为△ABC的内心，∠A=60°，CD=2，BD=4．则△DBC的面积是（）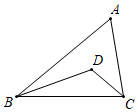

A、4 $\sqrt{3}$ B、2 $\sqrt{3}$ C、2 D、4

查看试题解析
9. 二次函数 $y = (x - a) (x - b) - 2 (a < b)$ 与x轴的两个交点的横坐标分别为m和n，且m ＜n，则下列结论正确的是（）

A、 $m < a < n < b$ B、 $a < m < b < n$ C、 $m < a < b < n$ D、 $a < m < n < b$

查看试题解析
10. 如图所示，在平面直角坐标系中，抛物线y=－x²＋2 $\sqrt{3}$ x的顶点为A点，且与x轴的正半轴交于点B，P点为该抛物线对称轴上一点，则OP＋ $\frac{1}{2}$ AP的最小值为（）.

A、3 B、 $2 \sqrt{3}$ C、 $\frac{3 + 2 \sqrt{21}}{4}$ D、 $\frac{3 + 2 \sqrt{3}}{2}$

查看试题解析

二、填空题

11. 比较大小：sin80°tan50°（填“＞”或“＜”）．

查看试题解析
12. 飞机着陆后滑行的距离s（单位：m）关于滑行的时间t（单位：s）的函数解析式是 $s = 20 t - 0.5 t^{2}$ ，飞机着陆后滑行m才能停下来.

查看试题解析
13. 如图，一根排水管道的横截面是半径为13cm的圆．排水管内有水，若水面宽度AB＝24cm，则水管中的水最大深度为 cm．

查看试题解析
14. 如图，点A，B，C在⊙O上，四边形OABC是平行四边形，若对角线AC＝2 $\sqrt{3}$ ，则 $\hat{A C}$ 的长为．

查看试题解析
15. 构建几何图形解决代数问题是“数形结合”思想的重要性，在计算tan15°时，如图，在Rt△ABC中，∠C＝90°，∠ABC＝30°，延长CB至D，使BD＝AB，连接AD，得∠D＝15°，所以tan15° $= \frac{A C}{C D} = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} =$ 2 $- \sqrt{3}$ ．类比这种方法，计算tan22.5°的值为．

查看试题解析
16. 已知二次函数y＝ax²＋bx＋c中，函数y与自变量x的部分对应值如下表：

x

…

－1

0

1

2

3

…

y

…

10

5

2

1

2

…

则当y＜5时，x的取值范围是.

查看试题解析
17. 我们定义一种新函数：形如y＝|ax²+bx+c|（a≠0，且b²﹣4ac＞0）的函数叫做“鹊桥”函数．小丽同学画出了“鹊桥”函数y＝|x²﹣2x﹣3|的图像（如图所示），并写出下列结论：
①图像与坐标轴的交点为（﹣1，0），（3，0）和（0，3）；
②图像具有对称性，对称轴是直线x＝1；
③当﹣1≤x≤1或x≥3时，函数值y随x值的增大而增大；
④当x＝﹣1或x＝3时，函数的最小值是0；
⑤当x＝1时，函数的最大值是4；
⑥若点P（a，b）在该图像上，则当b＝2时，可以找到4个不同的点P．其中错误的结论是（填序号）．

查看试题解析
18. 如图，在Rt△ABC中，∠C＝90°，AC＝9，BC＝4，以点C为圆心，3为半径做⊙C，分别交AC，BC于D，E两点，点P是⊙C上一个动点，则 $\frac{1}{3}$ PA+PB的最小值为．

查看试题解析

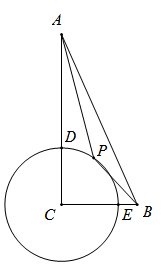
三、解答题

19. 计算：

(1)、2sin30°+3cos60°+tan45°；

(2)、 $| 1 - \sqrt{2} | - 2 c o s 4 5^{°} + (- \frac{1}{3})^{- 2}$ ．

查看试题解析
20. 如图，以40m/s的速度将小球沿与地面成30°角的方向击出时，小球的飞行路线将是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系h＝20t﹣5t² ．解答以下问题

(1)、小球从飞出到落地要用多少时间？

(2)、小球飞行的最大高度是多少？此时需要多少飞行时间？

查看试题解析
21. 避雷针是用来保护建筑物、高大树木等避免雷击的装置.如图，小陶同学要测量垂直于地面的大楼 $B C$ 顶部避雷针 $C D$ 的长度（ $B$ ， $C$ ， $D$ 三点共线），在水平地面 $A$ 点测得 $∠ C A B = 53 °$ ， $∠ D A B = 58 °$ ， $A$ 点与大楼底部 $B$ 点的距离 $A B = 20 m$ ，求避雷针 $C D$ 的长度.（结果精确到 $0.1 m$ .参考数据： $\sin 58 ° \approx 0.85$ ， $\cos 58 ° \approx 0.53$ ， $\tan 58 ° \approx 1.60$ ， $\sin 53 ° \approx 0.80$ ， $\cos 53 ° \approx 0.60$ ， $\tan 53 ° \approx 1.33$ ）

查看试题解析
22. 如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别与BC，AC交于点D，E，过点D作DF⊥AC，垂足为点F．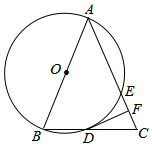

(1)、求证：直线DF是⊙O的切线；

(2)、求证：BD²＝CF•AC．

查看试题解析
23. 河上有一座桥孔为抛物线形的拱桥，水面宽6m时，水面离桥孔顶部3m.因降暴雨水位上升lm.

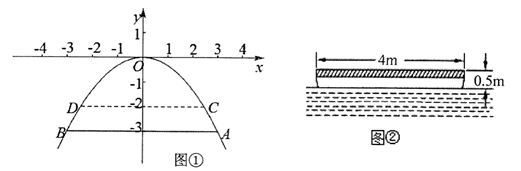(1)、如图①，若以桥孔的最高点为原点，建立平面直角坐标系，求抛物线的解析式；

(2)、一艘装满物资的小船，露出水面的高为0.5m、宽为4m（横断面如图②）.暴雨后这艘船能从这座拱桥下通过吗?请说明理由.

查看试题解析
24. 如图，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D，AB，DC的延长线交于点E．

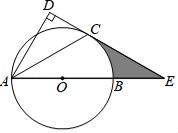(1)、求证：AC平分∠DAB；

(2)、若BE=3，CE=3 $\sqrt{3}$ ，求图中阴影部分的面积．

查看试题解析
25. 某景区超市销售一种纪念品，这种商品的成本价15元/件，已知销售价不低于成本价，且物价部门规定这种商品的销售价不高于24元/件，市场调查发现，该商品每天的销售量y（件）与销售单价x（元/件）之间的函数关系如图所示．

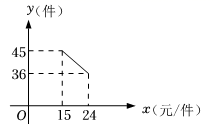(1)、求y与x之间的函数关系式，并写出自变量x的取值范围；

(2)、求每天的销售利润W（元）与销售单价x（元/件）之间的函数关系式，并求出每件销售价为多少元时，每天的销售利润最大？最大利润是多少？

查看试题解析
26. 如图，平行四边形ABCD中，AB+BC＝20，sinA $= \frac{4}{5}$ ， P是AB边上一点，设DC＝x，△PCD的面积为y．

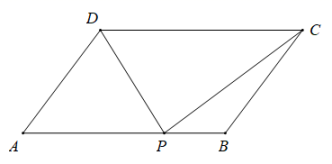(1)、求y与x的函数关系式，并求△PCD的面积的最大值；

(2)、若以DC为直径的圆过P、B两点，求CD的长．

查看试题解析
27. 如图，⊙O是△ABC的外接圆，AD是⊙O的直径，F是AD延长线上一点，连接CD，CF，且：CF是⊙O的切线．

(1)、求证：∠DCF＝∠CAD．

(2)、探究线段CF，FD，FA的数量关系并说明理由；

(3)、若cosB $= \frac{3}{5}$ ， AD＝2，求FD的长．

查看试题解析
28. 如图，在直角坐标系中，直线y＝ $\frac{1}{3}$ x+1与x轴、y轴的交点分别为A、B，以x＝﹣1为对称轴的抛物线y＝﹣x²+bx+c与x轴分别交于点A、C．

(1)、求抛物线的解析式；

(2)、若点P是第二象限内抛物线上的动点，设抛物线的对称轴l与x轴交于一点D，连接PD，交AB于E，求出当以A、D、E为顶点的三角形与△AOB相似时点P的坐标；

(3)、若点Q在第二象限内，且tan∠AQD＝2，线段CQ是否存在最小值？如果存在直接写出最小值，如果不存在，请说明理由．

查看试题解析

x	…	－1	0	1	2	3	…
y	…	10	5	2	1	2	…