辽宁省沈阳市浑南区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 如图所示的几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 关于x的一元二次方程 有两个不相等的实数根,则m的值可能是( )A、8 B、9 C、10 D、113. 用配方法解方程x2﹣4x﹣5=0时,原方程应变形为( )A、(x﹣2)2=9 B、(x﹣1)2=6 C、(x+1)2=6 D、(x+2)2=64. 如果两个相似多边形的周长比是2:3,那么它们的面积比为( )A、2:3 B、4:9 C、: D、16:815. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )
2. 关于x的一元二次方程 有两个不相等的实数根,则m的值可能是( )A、8 B、9 C、10 D、113. 用配方法解方程x2﹣4x﹣5=0时,原方程应变形为( )A、(x﹣2)2=9 B、(x﹣1)2=6 C、(x+1)2=6 D、(x+2)2=64. 如果两个相似多边形的周长比是2:3,那么它们的面积比为( )A、2:3 B、4:9 C、: D、16:815. 如图,在直角坐标系中,有两点A(6,3)、B(6,0).以原点O为位似中心,相似比为 ,在第一象限内把线段AB缩小后得到线段CD,则点C的坐标为( )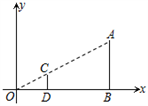 A、(2,1) B、(2,0) C、(3,3) D、(3,1)6. 有四张形状相同的卡片,正面分别印着矩形、菱形、等边三角形、圆四个图案,卡片背面全一样,随机抽出一张,刚好抽到正面的图案是中心对称图形的概率是( )A、 B、 C、 D、17. 在同一时刻的太阳光下,小刚的影子比小红的影子长,那么,在晚上同一路灯下( )A、不能够确定谁的影子长 B、小刚的影子比小红的影子短 C、小刚跟小红的影子一样长 D、小刚的影子比小红的影子长8. 关于菱形的性质,以下说法错误的是( )A、四条边相等 B、对角线相等 C、对角线互相垂直 D、是轴对称图形9. 抛物线的函数表达式为 ,若将 轴向上平移2个单位长度,将 轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为( )A、 B、 C、 D、10. 一次函数 的图象如图所示,则二次函数 的图象可能是( )
A、(2,1) B、(2,0) C、(3,3) D、(3,1)6. 有四张形状相同的卡片,正面分别印着矩形、菱形、等边三角形、圆四个图案,卡片背面全一样,随机抽出一张,刚好抽到正面的图案是中心对称图形的概率是( )A、 B、 C、 D、17. 在同一时刻的太阳光下,小刚的影子比小红的影子长,那么,在晚上同一路灯下( )A、不能够确定谁的影子长 B、小刚的影子比小红的影子短 C、小刚跟小红的影子一样长 D、小刚的影子比小红的影子长8. 关于菱形的性质,以下说法错误的是( )A、四条边相等 B、对角线相等 C、对角线互相垂直 D、是轴对称图形9. 抛物线的函数表达式为 ,若将 轴向上平移2个单位长度,将 轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的函数表达式为( )A、 B、 C、 D、10. 一次函数 的图象如图所示,则二次函数 的图象可能是( )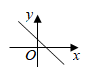 A、
A、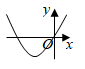 B、
B、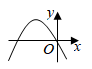 C、
C、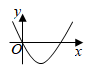 D、
D、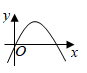
二、填空题
-
11. 关于x的一元二次方程x2+bx﹣10=0的一个根为2,则b的值为 .12. 已知==≠0,则的值为
13. 在一个不透明的袋子中有50个除颜色外均相同的小球,通过多次摸球试验后,发现摸到白球的频率约为36%,估计袋中白球有个.14. 如图,小明同学用自制的直角三角形纸板DEF测量树AB的高度,他调整自己的位置,使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=10m,则AB=m. 15. 如图,已知双曲线y= (k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k=.
15. 如图,已知双曲线y= (k>0)经过直角三角形OAB斜边OB的中点D,与直角边AB相交于点C.若△OBC的面积为3,则k=. 16. 如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3.其中正确结论的序号为 .
16. 如图,在正方形ABCD中,AB=4,E为对角线AC上与A,C不重合的一个动点,过点E作EF⊥AB于点F,EG⊥BC于点G,连接DE,FG,下列结论:①DE=FG;②DE⊥FG;③∠BFG=∠ADE;④FG的最小值为3.其中正确结论的序号为 .
三、解答题
-
17. 解方程:x2-7x-18=0.18. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,在DC的延长线上取一点E,连接OE交BC于点F,延长EO交AD于点G.
 (1)、求证:AOG≌COF;(2)、若AB=3,BC=4,CE=2,则CF= .19. 新年即将来临,利群商场为了吸引顾客,特别设计了一种促销活动:在一个不透明的箱子里放有4个除数字外完全相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.(1)、该顾客至少可得到元购物券;(2)、请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于40元的概率.20. 如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,且AD=AF.
(1)、求证:AOG≌COF;(2)、若AB=3,BC=4,CE=2,则CF= .19. 新年即将来临,利群商场为了吸引顾客,特别设计了一种促销活动:在一个不透明的箱子里放有4个除数字外完全相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.(1)、该顾客至少可得到元购物券;(2)、请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于40元的概率.20. 如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,且AD=AF. (1)、判断四边形ABFC的形状并证明;(2)、若AB=3,∠ABC=60°,求EF的长.21. 如图,一次函数 的图象与反比例函数 的图象交于 , 两点.
(1)、判断四边形ABFC的形状并证明;(2)、若AB=3,∠ABC=60°,求EF的长.21. 如图,一次函数 的图象与反比例函数 的图象交于 , 两点.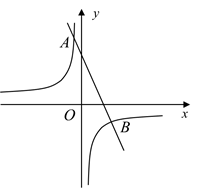 (1)、求一次函数和反比例函数的解析式;(2)、点 在 轴上,且满足 的面积等于4,请直接写出点 的坐标.22. 商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:(1)、商场日销售量增加件,每件商品盈利元(用含x的代数式表示);(2)、在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?23. 已知,如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(﹣9,3).
(1)、求一次函数和反比例函数的解析式;(2)、点 在 轴上,且满足 的面积等于4,请直接写出点 的坐标.22. 商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:(1)、商场日销售量增加件,每件商品盈利元(用含x的代数式表示);(2)、在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?23. 已知,如图,在平面直角坐标系内,点A的坐标为(0,12),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(﹣9,3). (1)、求直线l1 , l2的表达式;(2)、点C为直线OB上一动点(点C不与点O,B重合),作CDy轴交直线l2于点D,过点C,D分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.
(1)、求直线l1 , l2的表达式;(2)、点C为直线OB上一动点(点C不与点O,B重合),作CDy轴交直线l2于点D,过点C,D分别向y轴作垂线,垂足分别为F,E,得到矩形CDEF.①设点C的纵坐标为n,求点D的坐标(用含n的代数式表示);
②若矩形CDEF的面积为48,请直接写出此时点C的坐标.
24. 在菱形ABCD中,∠ABC=60°,P是直线BD上一动点,以AP为边向右侧作等边APE(A,P,E按逆时针排列),点E的位置随点P的位置变化而变化. (1)、如图1,当点P在线段BD上,且点E在菱形ABCD内部或边上时,连接CE,则BP与CE的数量关系是 , BC与CE的位置关系是;(2)、如图2,当点P在线段BD上,且点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;(3)、当点P在直线BD上时,其他条件不变,连接BE.若AB=2 , BE=2 , 请直接写出APE的面积.25. 如图,在平面直角坐标系中,已知抛物线y=ax2+2x+c(a≠0)与x轴交于点A,B,与y轴交于点C,连接BC,OA=1,OB=5,点D是此抛物线的顶点.
(1)、如图1,当点P在线段BD上,且点E在菱形ABCD内部或边上时,连接CE,则BP与CE的数量关系是 , BC与CE的位置关系是;(2)、如图2,当点P在线段BD上,且点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由;(3)、当点P在直线BD上时,其他条件不变,连接BE.若AB=2 , BE=2 , 请直接写出APE的面积.25. 如图,在平面直角坐标系中,已知抛物线y=ax2+2x+c(a≠0)与x轴交于点A,B,与y轴交于点C,连接BC,OA=1,OB=5,点D是此抛物线的顶点. (1)、求抛物线的表达式;(2)、抛物线上C,D两点之间的距离是;(3)、①点E是第一象限内抛物线上的动点,连接BE和CE,求BCE面积的最大值;
(1)、求抛物线的表达式;(2)、抛物线上C,D两点之间的距离是;(3)、①点E是第一象限内抛物线上的动点,连接BE和CE,求BCE面积的最大值;②在①的条件下,当BCE的面积最大时,P为y轴上一点,过点P作抛物线对称轴的垂线,垂足为M,连接ME,BP,探究EM+MP+PB是否存在最小值.若存在,请直接写出此时点M的坐标;若不存在,请说明理由.