辽宁省沈阳市沈北新区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 二次函数y=(x+2)2﹣1的顶点是( )A、(2,﹣1) B、(2,1) C、(﹣2,﹣1) D、(﹣2,1)2. 点(﹣3,5)在反比例函数y=(k≠0)的图象上,则下列各点在该函数图象上的是( )A、(5,﹣3) B、(﹣ , 3) C、(﹣5,﹣3) D、( , 3)3. 在Rt△ABC中,∠C=90°,AC=4,BC=3,则下列选项正确的是( )A、sinA= B、cosA= C、cosB= D、tanB=4. 菱形ABCD的周长是8cm,∠ABC=60°,那么这个菱形的对角线BD的长是( )A、cm B、2cm C、1cm D、2cm5. 如图,AB∥CD∥EF,若= , BD=9,则DF的长为( )
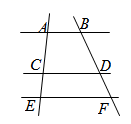 A、2 B、4 C、6 D、86. 将分别标有“中”“国”“加”“油”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀随机摸出一球,不放回;再随机摸出一球.两次摸出的球上的汉字能组成“加油”的概率是( )A、 B、 C、 D、7. 如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( )
A、2 B、4 C、6 D、86. 将分别标有“中”“国”“加”“油”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀随机摸出一球,不放回;再随机摸出一球.两次摸出的球上的汉字能组成“加油”的概率是( )A、 B、 C、 D、7. 如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=4,则BF的长为( ) A、4 B、8 C、2 D、48. 如图,在平面直角坐标系中,△OAB与△OCD位似,点O是它们的位似中心,已知A(﹣6,4),C(3,﹣2),则△OAB与△OCD的面积之比为( )
A、4 B、8 C、2 D、48. 如图,在平面直角坐标系中,△OAB与△OCD位似,点O是它们的位似中心,已知A(﹣6,4),C(3,﹣2),则△OAB与△OCD的面积之比为( ) A、1:1 B、2:1 C、3:1 D、4:19. 下列各组中两个图形不一定相似的是( )A、有一个角是35°的两个等腰三角形 B、两个等腰直角三角形 C、有一个角是120°的两个等腰三角形 D、两个等边三角形10. 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中错误的是( )
A、1:1 B、2:1 C、3:1 D、4:19. 下列各组中两个图形不一定相似的是( )A、有一个角是35°的两个等腰三角形 B、两个等腰直角三角形 C、有一个角是120°的两个等腰三角形 D、两个等边三角形10. 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论中错误的是( ) A、a﹣b+c>0 B、abc>0 C、4a﹣2b+c<0 D、2a﹣b=0
A、a﹣b+c>0 B、abc>0 C、4a﹣2b+c<0 D、2a﹣b=0二、填空题
-
11. 如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为 .
 12. 如图, 中, , , ,则 的面积是 .
12. 如图, 中, , , ,则 的面积是 .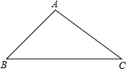 13. 如图,直线 与双曲线 交于点A , B . 过点A作 轴,垂足为点P , 连接 .若B的坐标为 ,则 .
13. 如图,直线 与双曲线 交于点A , B . 过点A作 轴,垂足为点P , 连接 .若B的坐标为 ,则 . 14. 在某市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为 ,由此可知该生此次实心球训练的成绩为米.15. 如图,ABC是一块锐角三角形的材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是mm.
14. 在某市中考体考前,某初三学生对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为 ,由此可知该生此次实心球训练的成绩为米.15. 如图,ABC是一块锐角三角形的材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是mm. 16. 如图,在矩形ABCD中,AB=3,BC=4,点P是对角线AC上一点,若点P、A、B组成一个等腰三角形时,△PAB的面积为 .
16. 如图,在矩形ABCD中,AB=3,BC=4,点P是对角线AC上一点,若点P、A、B组成一个等腰三角形时,△PAB的面积为 .
三、解答题
-
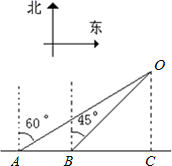
17. 解方程.(1)、2x2+3x=3.(2)、计算:4sin30°+2cos45°﹣tan60°﹣2.18. 在一个不透明的口袋中装有4个依次写有数字1,2,3,4的小球,它们除数字外都相同,每次摸球前都将小球摇匀.(1)、从中随机摸出一个小球,上面的数字不小于2的概率为 .(2)、从中随机摸出一球不放回,再随机摸出一球,请用列表或画树状图的方法,求两次摸出小球上的数字和恰好是奇数的概率.19. 如图,某船由西向东航行,在点A测得小岛O在北偏东60°,船航行了10海里后到达点B,这时测得小岛O在北偏东45°,船继续航行到点C时,测得小岛O恰好在船的正北方,求此时船到小岛的距离.
 20. 2019年某县投入100万元用于农村“扶贫工程”,计划以后每年以相同的增长率投入,2021年该县计划投入“扶贫工程”144万元.(1)、求该县投入“扶贫工程”的年平均增长率;(2)、若2022年保持从2019年到2021年的年平均增长率不变,求2022年该县将投入“扶贫工程”多少万元?21. 如图,边长为4的正方形ABCD,点E在AD边上,点F在CD边上,且AE=2,DF=1.
20. 2019年某县投入100万元用于农村“扶贫工程”,计划以后每年以相同的增长率投入,2021年该县计划投入“扶贫工程”144万元.(1)、求该县投入“扶贫工程”的年平均增长率;(2)、若2022年保持从2019年到2021年的年平均增长率不变,求2022年该县将投入“扶贫工程”多少万元?21. 如图,边长为4的正方形ABCD,点E在AD边上,点F在CD边上,且AE=2,DF=1. (1)、求BE的长;(2)、请判断△BEF的形状,并说明理由.22. 如图,矩形ABCD的顶点A,B在x轴的正半轴上,点B在点A的右侧,反比例函数在第一象限内的图象与直线交于点D,且反比例函数交BC于点E,AD=3.
(1)、求BE的长;(2)、请判断△BEF的形状,并说明理由.22. 如图,矩形ABCD的顶点A,B在x轴的正半轴上,点B在点A的右侧,反比例函数在第一象限内的图象与直线交于点D,且反比例函数交BC于点E,AD=3. (1)、求D点的坐标及反比例函数的关系式;(2)、若矩形的面积是24,求出△CDE的面积.(3)、直接写出当x>4时,y1的取值范围 .23. 如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G.
(1)、求D点的坐标及反比例函数的关系式;(2)、若矩形的面积是24,求出△CDE的面积.(3)、直接写出当x>4时,y1的取值范围 .23. 如图,点E是平行四边形ABCD对角线AC上一点,点F在BE延长线上,且EF=BE,EF与CD交于点G. (1)、求证:DF∥AC;(2)、连接DE、CF,若2AB=BF,且G恰好是CD的中点,求证:四边形CFDE是矩形;(3)、在(2)的条件下,若四边形CFDE是正方形,且BC=80,求AB的长.24. 如图,已知点P在矩形ABCD外,∠APB=90°,PA=PB,点E,F分别在AD,BC上运动,且∠EPF=45°,连接EF.
(1)、求证:DF∥AC;(2)、连接DE、CF,若2AB=BF,且G恰好是CD的中点,求证:四边形CFDE是矩形;(3)、在(2)的条件下,若四边形CFDE是正方形,且BC=80,求AB的长.24. 如图,已知点P在矩形ABCD外,∠APB=90°,PA=PB,点E,F分别在AD,BC上运动,且∠EPF=45°,连接EF. (1)、求证:△APE∽△BFP;(2)、当∠PEF=90°,AE=2时,
(1)、求证:△APE∽△BFP;(2)、当∠PEF=90°,AE=2时,①求AB的长;
②直接写出EF的长;
(3)、直接写出线段AE、BF、EF之间的数量关系.25. 如图,抛物线y=ax2+bx+2交x轴于点A(﹣3,0)和点B(1,0),交y轴于点C. (1)、求该抛物线的解析式;(2)、点D的坐标为(﹣1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值;(3)、抛物线对称轴上是否存在点M,使△MAB是以AB为斜边的直角三角形,若存在,请直接写出点M的坐标;若不存在,并说明理由;(4)、在对称轴上是否存在点N,使△BCN为直角三角形,若存在,直接写出N点坐标,若不存在,说明理由.
(1)、求该抛物线的解析式;(2)、点D的坐标为(﹣1,0),点P为第二象限内抛物线上的一个动点,求四边形ADCP面积的最大值;(3)、抛物线对称轴上是否存在点M,使△MAB是以AB为斜边的直角三角形,若存在,请直接写出点M的坐标;若不存在,并说明理由;(4)、在对称轴上是否存在点N,使△BCN为直角三角形,若存在,直接写出N点坐标,若不存在,说明理由.