上海市浦东新区多校联考2021-2022学年八年级上学期期末质量检测数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、2. 下列三个数为边长的三角形不是直角三角形的是( )A、3,3, B、4,8, C、6,8,10 D、5,5,3. 已知函数中,在每个象限内,的值随的值增大而增大,那么它和函数在同一直角坐标平面内的大致图像是( ).A、
 B、
B、 C、
C、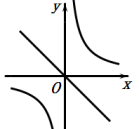 D、
D、 4. 下列命题中,逆命题错误的是( )A、两直线平行,同旁内角互补 B、对顶角相等 C、直角三角形的两个锐角互余 D、直角三角形两条直角边的平方和等于斜边的平方5. 如图,在等腰中, , , BD平分 , 交AC于点D, , 若cm,则的周长为( )
4. 下列命题中,逆命题错误的是( )A、两直线平行,同旁内角互补 B、对顶角相等 C、直角三角形的两个锐角互余 D、直角三角形两条直角边的平方和等于斜边的平方5. 如图,在等腰中, , , BD平分 , 交AC于点D, , 若cm,则的周长为( ) A、8cm B、10cm C、12cm D、14cm6. 在反比例函数y=的图像上有三点A1(x1 , y1)、A2(x2 , y2)、A3(x3 , y3),已知x1< x2<0<x3则下列各式中,正确的是( )A、y1<y2<y3 B、y3< y2< y1 C、y2< y1< y3 D、y3< y1< y2
A、8cm B、10cm C、12cm D、14cm6. 在反比例函数y=的图像上有三点A1(x1 , y1)、A2(x2 , y2)、A3(x3 , y3),已知x1< x2<0<x3则下列各式中,正确的是( )A、y1<y2<y3 B、y3< y2< y1 C、y2< y1< y3 D、y3< y1< y2二、填空题
-
7. 已知函数 , 那么 .8. 计算: .9. 函数 的定义域是 .10. 已知关于x的方程有两个不相等的实数根,那么m的取值范围是 .11. 随着网络购物的兴起,增加了快递公司的业务量,一家今年刚成立的小型快递公司业务量逐月攀升,今年9月份和11月份完成投送的快递件数分别是20万件和24.2万件,若该公司每月投送的快递件数的平均增长是x,由题意列出关于x的方程: .12. 在实数范围内因式分解:2x2﹣4x﹣1= .13. 到点A的距离等于6cm的点的轨迹是 .14. 已知:点A的坐标为 , 点B坐标为 , 那么点A和点B两点间的距离是 .15. 已知:如图,在中, , 线段AB的垂直平分线分别交AB、AC于点D、E,如果 , 那么 .
 16. 如图,在中, , 三角形的两个外角和的平分线交于点E.则 .
16. 如图,在中, , 三角形的两个外角和的平分线交于点E.则 . 17. 如图,P是正方形ABCD内一点,将绕点B顺时针方向旋转,能与重合,若 , 则 .
17. 如图,P是正方形ABCD内一点,将绕点B顺时针方向旋转,能与重合,若 , 则 . 18. 如图,直线AB与x轴交于点 , 与x轴夹角为30°,将沿直线AB翻折,点O的对应点C恰好落在双曲线上,则k的值为 .
18. 如图,直线AB与x轴交于点 , 与x轴夹角为30°,将沿直线AB翻折,点O的对应点C恰好落在双曲线上,则k的值为 .
三、解答题
-
19. 计算: .20. 解方程:21. 已知 , 并且与x成正比例,与成反比例.当时,;当时, , 求:y关于x的函数解析式.22. 某中学初二年级游同学在学习了勾股定理后对《九章算术》勾股章产生了学习兴趣.今天,他学到了勾股章第7题:“今有立木,系索其末,委地三尺,引索却行,去本八尺而索尽.问索长几何?”本题大意是:如图,木柱 , 绳索AC比木柱AB长三尺,BC的长度为8尺,求:绳索AC的长度.
 23. 初二年级小王同学坚持环保理念,每天骑自行车上学,学校离家3000米.某天,小王上学途中因自行车发生故障,修车耽误了一段时间后继续骑行,还是按时赶到了学校,如图描述的是他离家的距离S和离家的时间t之间的函数图象,根据图像解决下列问题:
23. 初二年级小王同学坚持环保理念,每天骑自行车上学,学校离家3000米.某天,小王上学途中因自行车发生故障,修车耽误了一段时间后继续骑行,还是按时赶到了学校,如图描述的是他离家的距离S和离家的时间t之间的函数图象,根据图像解决下列问题: (1)、修车时间为分钟:(2)、到达学校时共用时间分钟;(3)、小王从离家时到自行车发生故障时,离家的距离S和离家的时间t之间的函数关系式为定义域为;(4)、自行车故障排除后他的平均速度是每分钟米.24. 如图,已知.
(1)、修车时间为分钟:(2)、到达学校时共用时间分钟;(3)、小王从离家时到自行车发生故障时,离家的距离S和离家的时间t之间的函数关系式为定义域为;(4)、自行车故障排除后他的平均速度是每分钟米.24. 如图,已知. (1)、根据要求作图:在边上求作一点 , 使得点到、的距离相等,在边上求作一点 , 使得点到点、的距离相等;(不需要写作法,但需要保留作图痕迹和结论)(2)、在第(1)小题所作出的图中,求证:.25. 中, , 点D、E分别为边AB、BC上的点,且 , , 联结AE交CD与点F,点M是AE的中点,联结CM并延长与AB交于点H.
(1)、根据要求作图:在边上求作一点 , 使得点到、的距离相等,在边上求作一点 , 使得点到点、的距离相等;(不需要写作法,但需要保留作图痕迹和结论)(2)、在第(1)小题所作出的图中,求证:.25. 中, , 点D、E分别为边AB、BC上的点,且 , , 联结AE交CD与点F,点M是AE的中点,联结CM并延长与AB交于点H. (1)、点F是CD中点时,求证:;(2)、求证:26. 如图,在平面直角坐标系内,双曲线上有A,B两点,且与直线交于第一象限内的点A,点A的坐标为 , 点B的坐标为 , 过点B作y轴的平行线,交x轴于点C,交直线与点D.
(1)、点F是CD中点时,求证:;(2)、求证:26. 如图,在平面直角坐标系内,双曲线上有A,B两点,且与直线交于第一象限内的点A,点A的坐标为 , 点B的坐标为 , 过点B作y轴的平行线,交x轴于点C,交直线与点D. (1)、求:点D的坐标;(2)、求:的面积;(3)、在x轴正半轴上是否存在点P,使是以OA为腰的等腰三角形?若不存在,请说明理由;若存在,请直接写出P的坐标.27. 如图,中, , , . 点P是射线CB上的一点(不与点B重合),EF是线段PB的垂直平分线,交PB与点F,交射线AB与点E,联结PE、AP.
(1)、求:点D的坐标;(2)、求:的面积;(3)、在x轴正半轴上是否存在点P,使是以OA为腰的等腰三角形?若不存在,请说明理由;若存在,请直接写出P的坐标.27. 如图,中, , , . 点P是射线CB上的一点(不与点B重合),EF是线段PB的垂直平分线,交PB与点F,交射线AB与点E,联结PE、AP. (1)、求的度数;(2)、当点P在线段CB上时,设 , 的面积为y,求y关于x的函数解析式,并写出函数的定义域;(3)、如果 , 请直接写出的面积.
(1)、求的度数;(2)、当点P在线段CB上时,设 , 的面积为y,求y关于x的函数解析式,并写出函数的定义域;(3)、如果 , 请直接写出的面积.