山西省临汾市襄汾县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中是无理数的是（）

A、3.14 B、 $\sqrt{9}$ C、 $\sqrt{3}$ D、 $\frac{1}{7}$

查看试题解析
2. 以下命题是假命题的是（）

A、 $\sqrt{4}$ 的算术平方根是2 B、有两边相等的三角形是等腰三角形 C、三角形三个内角的和等于180° D、过直线外一点有且只有一条直线与已知直线平行

查看试题解析
3. 到三角形三边的距离都相等的点是三角形的（）

A、三条角平分线的交点 B、三条边的中线的交点 C、三条高的交点 D、三条边的垂直平分线的交点

查看试题解析
4. 某月1日—10日，甲、乙两人的手机“微信运动”的步数统计图如图所示，则下列错误的结论是（）

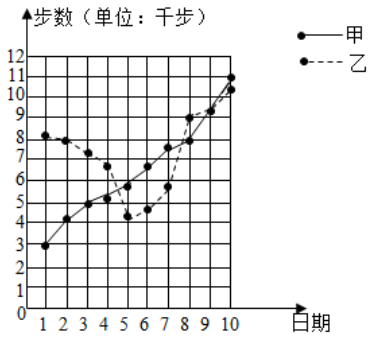A、1日—10日，甲的步数逐天增加 B、1日—6日，乙的步数逐天减少 C、第9日，甲、乙两人的步数正好相等 D、第11日，甲的步数不一定比乙的步数多

查看试题解析
5. △ABC的三边为a，b，c且（a＋b）（a﹣b）＝c² ，则该三角形是（）

A、锐角三角形 B、以c为斜边的直角三角形 C、以b为斜边的直角三角形 D、以a为斜边的直角三角形

查看试题解析
6. 其社区针对5月30日前该社区居民接种新冠疫苗的情况开展了问卷调查，共收回6000份有效问卷.经统计，制成如下数据表格.

接种疫苗针数

0

1

2

3

人数

2100

2280

1320

300

小杰同学选择扇形统计图分析接种不同针数的居民人数所占总人数的百分比.下面是制作扇形统计图的步骤（顺序打乱）：

①计算各部分扇形的圆心角分别为 $126 °$ ， $136.8 °$ ， $79.2 °$ ， $18 °$ .②计算出接种不同针数的居民人数占总人数的百分比分别为35%，38%，22%，5%.③在同一个圆中，根据所得的圆心角度数画出各个扇形，并注明各部分的名称及相应的百分比.制作扇形统计图的步骤排序正确的是（）

A、②①③ B、①③② C、①②③ D、③①②

查看试题解析
7. 我国是最早了解勾股定理的国家之一，它被记载于我国古代的数学著作《周髀算经》中．汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称之为“赵爽弦图”．现在勾股定理的证明已经有400多种方法，下面的两个图形就是验证勾股定理的两种方法，在验证著名的勾股定理过程，这种根据图形直观推论或验证数学规律和公式的方法，简称为 “无字证明”．在验证过程中它体现的数学思想是（）

A、函数思想 B、数形结合思想 C、分类思想 D、统计思想

查看试题解析
8. 若 $x + y = 6$ ， $x^{2} + y^{2} = 20$ ，求 $x y$ 的值是（）

A、6 B、8 C、26 D、20

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，根据尺规作图的痕迹，判断以下结论错误的是（）

A、 $∠ B D E = ∠ B A C$ B、 $∠ B A D = ∠ B$ C、 $D E = D C$ D、 $A E = A C$

查看试题解析
10. 如图，“赵爽弦图”是吴国的赵爽创制的．以直角三角形的斜边为边长得到一个正方形，该正方形由4个全等的直角三角形再加上中间的小正方形组成，在一次游园活动中，数学小组制作了一面“赵爽弦图锣”，其中 $∠ A B C = 90 °$ ， $A C = 13 c m$ ， $A B = 5 c m$ ，则阴影部分的面积是（） $c m^{2}$

A、169 B、25 C、49 D、64

查看试题解析

二、填空题

11. 计算 $\sqrt[3]{- 8} + \sqrt{36} - \sqrt{49} =$ ；

查看试题解析
12. 用反证法证明：在一个三角形中，如果两个角不相等，那么这两个角所对的边也不相等，证明时，可以先假设：．

查看试题解析
13. 如图，△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=40°，则∠CDE的度数为．

查看试题解析
14. 如图，在 $△ A B C$ 中，AD是 $∠ B A C$ 的平分线， $A B = 10 c m$ ， $A C = 8 c m$ ，则 $S_{△ A B D} ： S_{△ A C D} =$ ．

查看试题解析
15. 如图，在长方形ABCD中， $D C = 9$ ．在DC上找一点E，沿直线AE把 $△ A E D$ 折叠，使D点恰好落在BC上，设这一点为F，若 $△ A B F$ 的面积是54，则 $△ F C E$ 的面积= ．

查看试题解析

三、解答题

16. 因式分解

(1)、 $a^{3} b - a b$

(2)、 ${(x^{2} + 4)}^{2} - 16 x^{2}$

查看试题解析
17. 先化简，再求值： $[{(x - 2 y)}^{2} + (x - 2 y) (x + 2 y) - 2 x (2 x - y)] \div 2 x$ ，其中 $x = 1$ ， $y = \frac{1}{2}$ ．

查看试题解析

18. 国务院教育督导委员会办公室印发的《关于组织责任督学进行“五项管理”督导的通知》指出，要加强中小学生作业、睡眠、手机、读物、体质管理.某校数学社团成员采用随机抽样的方法，抽取了八年级部分学生，对他们一周内平均每天的睡眠时间

t

（单位：

h

）进行了调查，将数据整理后得到下列不完整的统计图表：

组别	睡眠时间分组	频数	频率
$A$	$t < 6$	4	0.08
$B$	$6 \leq t < 7$	8	0.16
$C$	$7 \leq t < 8$	10	$a$
$D$	$8 \leq t < 9$	21	0.42
$E$	$t \geq 9$	$b$	0.14

请根据图表信息回答下列问题：

(1)、频数分布表中，

a =

，

b =

；

(2)、扇形统计图中，

C

组所在扇形的圆心角的度数是

°

；

(3)、请估算该校600名八年级学生中睡眠不足7小时的人数；

(4)、研究表明，初中生每天睡眠时长低于7小时，会严重影响学习效率.请你根据以上调查统计结果，向学校提出一条合理化的建议.

查看试题解析

19. 如图，在△ABC中，点E是AB延长线上一点，且BE＝AB．

(1)、尺规作图：在∠CBE内作射线BD，使BD∥AC．（保留作图痕迹，不要求写作法）

(2)、在BD上取点F，使BF＝AC，连接EF，求证△ABC≌△BEF．

查看试题解析
20. 在甲村至乙村的公路旁有一块山地正在开发，现有一C处需要爆破．已知点C与公路上的停靠站A的距离为500米，与公路上另一停靠站B的距离为1200米，且CA⊥CB，如图，为了安全起见，爆破点C周围半径400米范围内不得进入．问在进行爆破时，公路AB段是否有危险，是否需要暂时封锁？请通过计算进行说明．

查看试题解析
21. 教材呈现：如图是华师版八年级上册数学教材第94页的部分内容．请根据教材中的分析．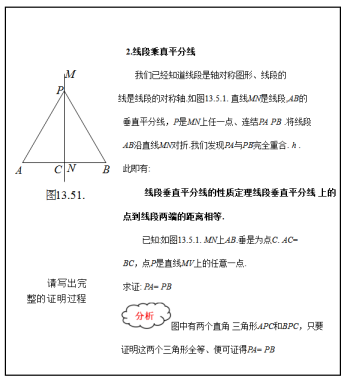

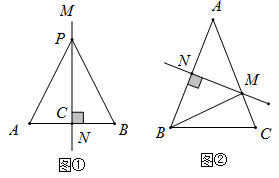(1)、结合图①，写出“线段的垂直平分线质定理”完整的证明过程．

(2)、定理应用：
如图②，在 $△ A B C$ 中， $A B = A C$ ， AB的垂直平分线交AB于N，交AC于M．连接MB，若AB=8cm， $△ M B C$ 的周长是14cm．
①求BC的长；
②点P是直线MN上一动点，在运动的过程中，由P，B，C构成的 $△ P B C$ 的周长是否存在最小值?若存在，标出点P的位置，并求 $△ P B C$ 的周长最小值；若不存在，说明理由．

查看试题解析
22. 阅读与思考
配方法是指将一个式子或一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和．巧妙的运用“配方法”能对一些多项式进行因式分解．
例如： $x^{2} + 4 x - 5 = x^{2} + 4 x + 2^{2} - 2^{2} - 5 = {(x + 2)}^{2} - 9 = (x + 2 + 3) (x + 2 - 3) = (x + 5) (x - 1)$

(1)、解决问题：运用配方法将下列多项式进行因式分解
① $x^{2} + 3 x - 4$ ；
② $x^{2} - 8 x - 9$

(2)、深入研究：说明多项式 $x^{2} - 6 x + 12$ 的值总是一个正数?

(3)、拓展运用：已知a、b、c分别是 $△ A B C$ 的三边，且 $a^{2} - 2 a b + 2 b^{2} - 2 b c + c^{2} = 0$ ，试判断 $△ A B C$ 的形状，并说明理由．

查看试题解析
23. 已知△ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上的一动点（点D不与点B、C重合），以AD为边作△ADE，使∠DAE＝90°，AD＝AE，连接CE．

(1)、发现问题：
如图1，当点D在边BC上时，
请写出BD和CE之间的位置关系为，并猜想BC和CE、CD之间的数量关系：．

(2)、尝试探究：
如图2，当点D在边BC的延长线上且其他条件不变时，（1）中BD和CE之间的位置关系，BC和CE、CD之间的数量关系是否成立？若成立，请证明；若不成立，请写出新的数量关系，说明理由；

(3)、拓展延伸：
如图3，当点D在边CB的延长线上且其他条件不变时，若BC＝7，CE＝5，直接写出线段ED的长．

查看试题解析

接种疫苗针数	0	1	2	3
人数	2100	2280	1320	300