辽宁省沈阳市于洪区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 一个正方体的体积是5m³ ，则这个正方体的棱长是（）

A、 $\sqrt{5}$ m B、 $\sqrt[3]{5}$ m C、25m D、125m

查看试题解析
2. 如图，直线a，b被直线c所截，下列条件不能判定直线a与b平行的是（）

A、∠1＝∠3 B、∠2+∠3＝180° C、∠1＝∠4 D、∠1+∠4＝180°

查看试题解析
3. 在平面直角坐标系中，点P（2，5）关于y轴对称的点的坐标为（）

A、（2，﹣5） B、（﹣2，﹣5） C、（﹣2，5） D、（﹣5，2）

查看试题解析
4. 下列计算正确的是（）

A、 $\sqrt{16}$ ＝±4 B、 $\sqrt{(- 3)^{2}}$ ＝﹣3 C、3+4 $\sqrt{2}$ ＝7 $\sqrt{2}$ D、 $\sqrt{8}$ ﹣ $\sqrt{2}$ ＝ $\sqrt{2}$

查看试题解析
5. 已知△ABC的三边长分别为5，13，12，则△ABC的面积为（）

A、30 B、60 C、78 D、不能确定

查看试题解析
6. 某校“安全知识”比赛有16名同学参加，规定前8名的同学进入决赛．若某同学想知道自己能否晋级，不仅要了解自己的成绩，还需要了解16名参赛同学成绩的（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
7. 能说明命题“若x为无理数，则x²也是无理数”是假命题的反例是（）

A、 $x = \sqrt{2} - 1$ B、 $x = \sqrt{2} + 1$ C、 $x = 3 \sqrt{2}$ D、 $x = \sqrt{3} - \sqrt{2}$

查看试题解析
8. 一次函数y＝kx+b的图象如图所示，则下列说法错误的是（）

A、y随x的增大而减小 B、k＜0，b＜0 C、当x＞4时，y＜0 D、图象向下平移2个单位得y＝﹣ $\frac{1}{2}$ x的图象

查看试题解析
9. 小明带30元钱去买笔，钢笔5元一支和圆珠笔2元一支，买了两种笔，刚好用完这些钱，请问小明共有几种购买方法（）

A、4种 B、3种 C、2种 D、1种

查看试题解析

10. 定理：三角形的一个外角等于与它不相邻的两个内角的和．已知：如图，∠ACD是△ABC的外角．求证：∠ACD＝∠A+∠B．

证法1：如图，

∵∠A＝70°，∠B＝63°，

且∠ACD＝133°（量角器测量所得）

又∵133°＝70°+63°（计算所得）

∴∠ACD＝∠A+∠B（等量代换）．

证法2：如图，

∵∠A+∠B+∠ACB＝180°（三角形内角和定理），

又∵∠ACD+∠ACB＝180°（平角定义），

∴∠ACD+∠ACB＝∠A+∠B+∠ACB（等量代换）．

∴∠ACD＝∠A+∠B（等式性质）．

下列说法正确的是（）

A、证法1用特殊到一般法证明了该定理 B、证法1只要测量够100个三角形进行验证，就能证明该定理 C、证法2还需证明其他形状的三角形，该定理的证明才完整 D、证法2用严谨的推理证明了该定理

查看试题解析

二、填空题

11. 3的相反数是。

查看试题解析
12. 如图，直线 $a ∥ b$ ，三角尺（30°，60，90°）如图摆放，若∠1＝52°，则∠2的度数为．

查看试题解析
13. 设 $\sqrt{5}$ 的整数部分为 $a$ ， $\sqrt{13}$ 小数部分为 $b$ ，那么 $a + b =$ ．

查看试题解析
14. 已知点 $A (m ， - 2)$ ， $B (3 ， m - 1)$ ，且直线 $A B ∥ x$ 轴，则m的值是．

查看试题解析
15. 某品牌鞋的长度ycm与鞋的“码”数x之间满足一次函数关系．若22码鞋的长度为16cm，44码鞋的长度为27cm，则长度为23cm鞋的码数为．

查看试题解析
16. 如图，长方形纸片ABCD中，AB＝8cm，BC＝17cm，点O在边BC上，且OB＝10cm．将纸片沿过点O的直线折叠，若点B恰好落在边AD上的点F处，则AF的长为 cm．

查看试题解析

三、解答题

17. 解方程组： ${\begin{matrix} 3 x + 2 y = 14 \\ 5 x - y = 6 \end{matrix}$ ．

查看试题解析
18. 计算：

(1)、 $\sqrt{\frac{2}{3}} - \sqrt{\frac{3}{2}} + \sqrt{2} \times \sqrt{3}$ ；

(2)、（ $\sqrt{18} - \sqrt{10}$ ）÷ $\sqrt{2}$ +（1+ $\sqrt{5}$ ）² ．

查看试题解析
19. 如图，在 $4 \times 4$ 的正方形网格中，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形.

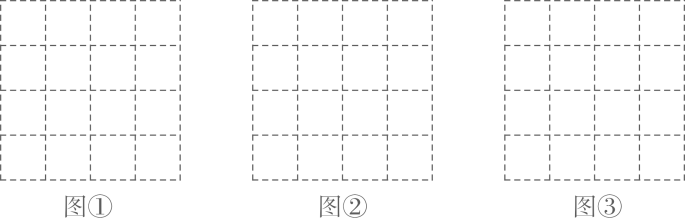(1)、在图①中，画一个直角三角形，使它的三边长都是有理数；

(2)、在图②中，画一个直角三角形，使它的一边长是有理数，另外两边长是无理数；

(3)、在图③中，画一个直角三角形，使它的三边长都是无理数.

查看试题解析
20. 甲、乙两名队员参加射击训练，将10次成绩分别制成如图所示的两个统计图：

(1)、根据以上信息，整理分析数据如表：

平均成绩（环）
众数（环）
中位数
方差
甲
7
a
7
c
乙
7
8
b
4.2
填空：a＝， b＝， c＝；

(2)、根据以上数据分析，请你运用所学统计知识，任选两个角度评价甲、乙两名队员哪位队员的射击成绩更好．

查看试题解析
21. 如图，∠MON＝90°，点A，B分别在OM，ON上，AE平分∠MAB，BE平分∠NBA．当点A，B在OM，ON上的位置变化时，∠E的大小是否变化？若∠E的大小保持不变，请说明理由；若∠E的大小变化，求出变化范围．

查看试题解析
22. 元旦前，某商店准备了两种价格分别为36元/kg和20元/kg的糖果混合成的杂拌糖果100kg．

(1)、若混合后糖果的定价为28元/kg，需要两种糖果各多少千克？

(2)、若将价格分别为36元/kg和20元/kg的糖果按2：3的比例混合并定价，则100kg杂拌糖果全部售出的销售额为元．

查看试题解析
23. 寒假将至，某健身俱乐部面向大中学生推出优惠活动，活动方案如下：
方案一：购买一张学生寒假专享卡，每次健身费用按六折优惠；
方案二：不购买学生寒假专享卡，每次健身费用按八折优惠．
设某学生健身x（次），按照方案一所需费用为y₁（元），且y₁＝k₁x+b；按照方案二所需费用为y₂（元），且y₂＝k₂x．在平面直角坐标系中的函数图象如图所示．

(1)、求k₁和b的值，并说明它们的实际意义；

(2)、求k₂的值；

(3)、八年级学生小华计划寒假前往该俱乐部健身8次，应选择哪种方案所需费用更少？请说明理由．

(4)、小华的同学小琳也计划在该俱乐部健身，若她准备300元的健身费用，最多可以健身多少次？

查看试题解析
24. 如图

(1)、如图1，四边形ABCD的对角线AC⊥BD于点O．判断AB²+CD²与AD²+BC²的数量关系，并说明理由．

(2)、如图2，分别以Rt△ABC的直角边AB和斜边AC为边向外作正方形ABDM和正方形ACEN，连接BN，CM，交点为O．
①判断CM，BN的关系，并说明理由．
②连接MN．若AB＝2，BC＝3，请直接写出MN的长．

查看试题解析
25. 在平面直角坐标系中，直线y＝kx+4（k≠0）交x轴于点A（8，0），交y轴于点B．

(1)、k的值是；

(2)、点C是直线AB上的一个动点，点D和点E分别在x轴和y轴上．
①如图，点D的坐标为（6，0），点E的坐标为（0，1），若四边形OECD的面积是9，求点C的坐标；
②当CE平行于x轴，CD平行于y轴时，若四边形OECD的周长是10，请直接写出点C的坐标．

查看试题解析

	平均成绩（环）	众数（环）	中位数	方差
甲	7	a	7	c
乙	7	8	b	4.2