辽宁省沈阳市铁西区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 4的平方根是（）

A、±2 B、﹣2 C、2 D、 $\sqrt{4}$

查看试题解析
2. 如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝40°，直线a∥b，若BC在直线b上，则∠1的度数为（）

A、40° B、45° C、50° D、60°

查看试题解析
3. 在如图所示的方格纸中，点A，B，C均为格点，则 $∠ A B C$ 的度数是（）

A、 $30 °$ B、 $35 °$ C、 $45 °$ D、 $60 °$

查看试题解析
4. 下列等式何者不成立（）

A、 $4 \sqrt{3} + 2 \sqrt{3} = 6 \sqrt{3}$ B、 $4 \sqrt{3} - 2 \sqrt{3} = 2 \sqrt{3}$ C、 $4 \sqrt{3} \times 2 \sqrt{3} = 8 \sqrt{3}$ D、 $4 \sqrt{3} \div 2 \sqrt{3} = 2$

查看试题解析
5. 用加减消元法解二元一次方程组 ${\begin{matrix} x + 3 y = 4 ① \\ 2 x - y = 1 ② \end{matrix}$ 时，下列方法中无法消元的是（）

A、①×2﹣② B、②×（﹣3）﹣① C、①×（﹣2）+② D、①﹣②×3

查看试题解析
6. 一把直尺与一块直角三角板按如图方式摆放，若∠1＝28°，则∠2＝（）

A、62° B、58° C、52° D、48°

查看试题解析

7. 某校为推荐一项作品参加“科技创新”比赛，对甲、乙、丙、丁四项候选作品进行量化评分，具体成绩（百分制）如表：

项目

作品

甲

乙

丙

丁

创新性

实用性

如果按照创新性占60%，实用性占40%计算总成绩，并根据总成绩择优推荐，那么应推荐的作品是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

8. 在平面直角坐标系中，O为坐标原点.若直线y＝x+3分别与x轴、直线y＝﹣2x交于点A、B，则△AOB的面积为（）

A、2 B、3 C、4 D、6

查看试题解析
9. 小明收集了鄂尔多斯市某酒店2021年3月1日～3月6日每天的用水量（单位：吨），整理并绘制成如图所示的折线统计图，下列结论正确的是（）

A、平均数是 $\frac{23}{4}$ B、众数是10 C、中位数是8.5 D、方差是 $\frac{25}{3}$

查看试题解析
10. 在平面直角坐标系中，点A的坐标为（﹣4，3），若AB∥x轴，且AB＝5，当点B在第二象限时，点B的坐标是（）

A、（﹣9，3） B、（﹣1，3） C、（1，﹣3） D、（1，3）

查看试题解析

二、填空题

11. 甲、乙两人在相同条件下进行射击练习，每人10次射击成绩的平均数都是8环，方差分别为S_甲²＝1.4，S_乙²＝0.6，则两人射击成绩比较稳定的是（填“甲”或“乙”）．

查看试题解析
12. 比较大小：2 $\sqrt{7}$ 5（填“＞”、“＝”或“＜”）．

查看试题解析
13. 二元一次方程组 ${\begin{array}{l} x - 4 y = 0 \\ 6 y - x = 10 \end{array}$ 的解为．

查看试题解析
14. 如图，AB∥CD∥EF，若∠ABC＝125°，∠CEF＝105°，则∠BCE的度数为．

查看试题解析
15. 已知一次函数y＝﹣2x﹣1的图象经过A(x₁ ， 1)，B(x₂ ， 3)两点，则x₁x₂（填“＞”“＜”或“＝”）.

查看试题解析
16. 同学们，我们在今后的学习中会学到这个定理：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．即：如图，在Rt△ABC中，∠ACB＝90°，若∠ABC＝30°，则 $A C = \frac{1}{2} A B$ ．问题：在Rt△ABC，∠ACB＝90°，∠ABC＝30°，AC＝ $\sqrt{3}$ ，点D是边BC的中点，点E是斜边AB上的动点，连接DE，把△BDE沿直线DE折叠，点B的对应点为点F．当直线DF⊥AB时，AE的长为．

查看试题解析

三、解答题

17. 计算： $(\sqrt{6} - 2 \sqrt{15}) \times \sqrt{3} - 6 \sqrt{\frac{1}{2}}$

查看试题解析
18. 如图，在△ABC中，∠B=40°，∠C=60°，AD、AE分别是角平分线和高．求∠DAE的度数．

查看试题解析
19. 已知方程组 ${\begin{array}{l} 2 x + y = 7 \\ x = y - 1 \end{array}$ 的解也是关于x、y的方程 $a x + y = 4$ 的一个解，求a的值.

查看试题解析
20. 已知点A（1，﹣1），B（﹣1，4），C（﹣3，1）．
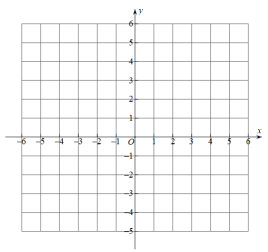
⑴请在如图所示的平面直角坐标系中（每个小正方形的边长都为1）画出△ABC；
⑵作△ABC关于x轴对称的△DEF，其中点A，B，C的对应点分别为点D，E，F；
⑶连接CE，CF，请直接写出△CEF的面积．

查看试题解析
21. 如图，在△ABC中，∠BAC＝90°，AB＝AC，射线AE交BC于点P，∠BAE＝15°；过点C作CD⊥AE于点D，连接BE，过点E作EF∥BC交DC的延长线于点F．

(1)、求∠F的度数；

(2)、若∠ABE＝75°，求证：BE∥CF．

查看试题解析
22. 某中学为了解八年学级生参加志愿者活动的次数，随机调查了该年级20名学生，统计得到该20名学生参加志愿者活动的次数如下：
3，5，3，6，3，4，4，5，2，4，5，6，1，3，5，5，4，4，2，4
根据以上数据，得到如下不完整的频数分布表：
次数
1
2
3
4
5
6
人数
1
2
a
6
b
2

(1)、表格中的a＝， b＝；

(2)、在这次调查中，参加志愿者活动的次数的众数为，中位数为；

(3)、若该校八年级共有700名学生，根据调查统计结果，估计该校八年级学生参加志愿者活动的次数大于4次的人数．

查看试题解析
23. 甲、乙两人沿同一直道从A地去B地，甲比乙早1min出发，乙的速度是甲的2倍．在整个行程中，甲离A地的距离y₁（单位：m）与时间x（单位：min）之间的函数关系如图所示．

(1)、求乙离A地的距离y₂（单位：m）与时间x（单位：min）之间的函数关系式；并在图中画出乙离A地的距离y₂（单位：m）与时间x（单位：min）之间的函数图象；

(2)、若甲比乙晚5min到达B地，求乙整个行程所用的时间．

查看试题解析
24. 为响应政府号召，某地水果种植户借助电商平台，在线下批发的基础上同步在电商平台上零售水果．已知线上零售40千克，线下批发80千克水果共获得4000元；线上零售60千克和线下批发80千克水果销售额相同．

(1)、求线上零售和线下批发水果的单价分别为每千克多少元？

(2)、若该地区水果种植户张大叔某月线上零售和线下批发共销售水果2000千克，设线上零售m千克．获得的总销售额为w元．
①求w与m之间的函数关系式；
②若总销售额为70000元，则线上零售量为多少千克？

查看试题解析
25. 已知等边三角形ABC，过点B作MN⊥AB于点B，点D是直线MN上的动点（不与点B重合），连接AD，以AD为边在AD的右侧作等边三角形ADE，连接CE，直线CE交MN于点F．

(1)、如图，当点D，E在直线AB的两侧时，
①求证：BD＝CE；
②求∠BCE的度数；

(2)、若AB＝BD，请直接写出 $\frac{C D}{A E}$ 的值；

(3)、若EF：CF＝3：2，△BDE的面积为4 $\sqrt{3}$ ，请直接写出BD的长．

查看试题解析

次数	1	2	3	4	5	6
人数	1	2	a	6	b	2