辽宁省沈阳市浑南区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、±2 B、2 C、-2 D、 $\pm \sqrt{2}$

查看试题解析
2. 下列各点位于平面直角坐标系内第二象限的是（）

A、 $(1 ， 2)$ B、 $(- 1 ， 2)$ C、 $(1 ， - 2)$ D、 $(- 1 ， - 2)$

查看试题解析
3. 以下正方形的边长是无理数的是（）

A、面积为9的正方形 B、面积为49的正方形 C、面积为8的正方形 D、面积为25的正方形

查看试题解析
4. 下列各式中正确的是（）

A、 $\sqrt{{(- 7)}^{2}} = - 7$ B、 $\sqrt{9} = \pm 3$ C、 $\sqrt{{(- 2)}^{2}} = 4$ D、 $\sqrt{48} - \sqrt{3} = 3 \sqrt{3}$

查看试题解析
5. 如图，在平面直角坐标系中，直线l₁： $y = x + 3$ 与直线l₂： $y = m x + n$ 交于点A（ $- 1$ ，b），则关于x、y的方程组 ${\begin{array}{l} y = x + 3 \\ y = m x + n \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 2 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = - 2 \end{array}$

查看试题解析
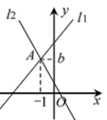6. 下列各组数中，能作为直角三角形三边长的是（）

A、1，2， $\sqrt{5}$ B、8，9，10 C、 $\sqrt{5}$ ， $2 \sqrt{3}$ ， $\sqrt{13}$ D、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$

查看试题解析
7. 某商店售货时，在进价基础上加一定利润，其数量 x与售价 y如下表所示，则售价 y与数量 x的函数关系式为（）
数量x（千克）
1
2
3
4
…
售价y（元）
8+0.4
16+0.8
24+1.2
32+1.6
…

A、y=8+0.4x B、y=8x+0.4 C、y=8.4x D、y=8.4x+0.4

查看试题解析
8. 某校八年级人数相等的甲、乙、丙三个班，同时参加了一次数学测试，对成绩进行了统计分析，平均分都是72分，方差分别为 $S_{甲}^{2} = 206$ ， $S_{乙}^{2} = 198$ ， $S_{丙}^{2} = 156$ ，则成绩波动最小的班级（）

A、甲 B、乙 C、丙 D、无法确定

查看试题解析
9. 估计 $\sqrt{10}$ +1的值应在（）

A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间

查看试题解析
10. 下列命题是假命题的是（）

A、同旁内角互补，两直线平行； B、如果两条直线都和第三条直线平行，那么这两条直线也互相平行； C、同一平面内，如果两条直线都垂直于同一条直线，那么这两条直线平行； D、同位角互补，两直线平行；

查看试题解析

二、填空题

11. 已知点M坐标为 $(- 4 ， - 7)$ ，点M到x轴距离为．

查看试题解析
12. 已知一次函数y=kx+b的图象经过A（1，﹣1），B（﹣1，3）两点，则k0（填“＞”或“＜”）

查看试题解析
13. 某单位拟招聘一个管理员，其中某位考生笔试、试讲、面试三轮测试得分分别为92分，85分，90分，若依次按40%，40%，20%的比例确定综合成绩，则该名考生的综合成绩为分．

查看试题解析
14. 如图所示，有一个高18cm，底面周长为24cm的圆柱形玻璃容器，在外侧距下底1cm的点S处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一只苍蝇，则急于捕获苍蝇充饥的蜘蛛所走的最短路径的长度是.

查看试题解析
15. 如图， $△ A B C$ 的顶点都在正方形网格的格点上，点A的坐标为 $(- 1 ， 4)$ ，将 $△ A B C$ 沿坐标轴翻折，则点C的对应点 $C$ 的坐标是．

查看试题解析
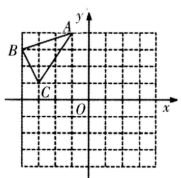16. 如图，四边形ABCD， $A B ⊥ B C$ ， $A B ∥ C D$ ， $A B = B C = 4$ ， $C D = 2$ ，点F为BC边上一点，且 $C F = 1$ ，连接AF， $D G ⊥ A F$ 垂足为E，交BC于点G，则BG的长为．

查看试题解析

三、解答题

17. 计算： ${(π - 2)}^{0} + | \sqrt{5} - 2 | + 6 \times \frac{\sqrt{5}}{2} + \sqrt[3]{64}$

查看试题解析
18.

(1)、 $\sqrt{18} \times \sqrt{2} - \frac{\sqrt{98}}{\sqrt{2}}$

(2)、 ${(\sqrt{3} - 2)}^{2} - \frac{\sqrt{54} - \sqrt{24}}{\sqrt{2}}$

查看试题解析
19. 选用适当的方法解方程组： ${\begin{cases} 2 x - y = 3 \\ 3 x + 2 y = 8 \end{cases}$

(1)、本题你选用的方法是；

(2)、写出你的解题过程．

查看试题解析
20. 甲、乙两校参加区举办的学生英语口语竞赛，两校参赛人数相等．比赛结束后，统计学生成绩分别为7分、8分、9分、10分（满分为10分）．依据统计数据绘制了如下尚不完整的统计图和统计表：
甲校成绩统计表
成绩
7分
8分
9分
10分
人数
11
0
x
8

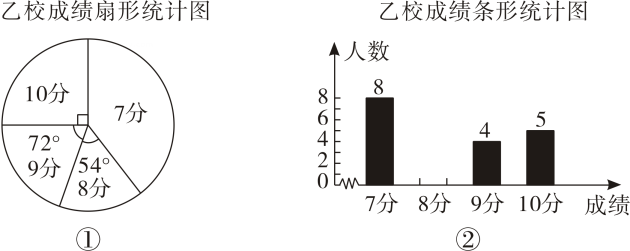(1)、甲校参赛人数是人， $x =$ ；

(2)、请你将如图②所示的统计图补充完整；

(3)、请分别求出甲校和乙校学生成绩的平均数和中位数，并从平均数和中位数的角度分析哪个学校的成绩较好？

查看试题解析
21. 已知：如图，直线 $M N ∥ H Q$ ，直线MN交EF，PO于点A，B，直线HQ交EF，PO于点D，C，DG与OP交于点G，若 $∠ 1 = 103 °$ ， $∠ 2 = 77 °$ ， $∠ 3 = 96 °$ ．

(1)、求证： $E F ∥ O P$ ；

(2)、请直接写出 $∠ C D G$ 的度数．

查看试题解析
22. 如图，用 10 块相同的小长方形地砖拼成一个宽是 75 厘米的大长方形，用列方程或方程组的方法，求每块小长方形地砖的长和宽分别是多少厘米？

查看试题解析
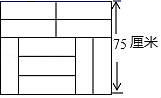23. 某水果店进行了一次水果促销活动，在该店一次性购买A种水果的单价y（元）与购买量x（千克）的函数关系如图所示，

(1)、当 $0 < x \leq 5$ 时，单价y为元；当单价y为8.8元时，购买量x（千克）的取值范围为；

(2)、根据函数图象，当 $5 \leq x \leq 11$ 时，求出函数图象中单价y（元）与购买量x（千克）的函数关系式；

(3)、促销活动期间，张亮计划去该店购买A种水果10千克，那么张亮共需花费多少元？

查看试题解析
24. $△ A B C$ 中，CD平分 $∠ A C B$ ，点E是BC上一动点，连接AE交CD于点D．

(1)、如图1，若 $∠ A D C = 110 °$ ， AE平分 $∠ B A C$ ，则 $∠ B$ 的度数为；

(2)、如图2，若 $∠ A D C = 100 °$ ， $∠ D C E = 53 °$ ， $∠ B - ∠ B A E = 27 °$ ，则 $∠ B A E$ 的度数为；

(3)、如图3，在BC的右侧过点C作 $C F ⊥ C D$ ，交AE延长线于点F，且 $A C = C F$ ， $∠ B = 2 ∠ F$ ．试判断AB与CF的位置关系，并证明你的结论．

查看试题解析
25. 如图，在平面直角坐标系xOy中， $△ O A B$ 的顶点O是坐标原点，点A在第一象限，点B在x轴的正半轴上， $∠ O A B = 90 °$ 且 $O A = A B$ ， $O B = 6$ ，点C是直线OC上一点，且在第一象限， $O B$ ， $O C$ 满足关系式 $O B + \sqrt{10} O C = 26$ ．

(1)、请直接写出点A的坐标；

(2)、点P是线段OB上的一个动点（点P不与点O重合），过点P的直线l与x轴垂直，直线l交边 $O A$ 或边AB于点Q，交OC于点R．设点P的横坐标为t，线段QR的长度为m．当 $t = 6$ 时，直线l恰好过点C．
①求直线OC的函数表达式；
②当 $m = \frac{3}{4}$ 时，请直接写出点P的坐标；
③当直线RQ与直线OC所组成的角被射线RA平分时，请直接写出t的值．

查看试题解析

数量x（千克）	1	2	3	4	…
售价y（元）	8+0.4	16+0.8	24+1.2	32+1.6	…

成绩	7分	8分	9分	10分
人数	11	0	x	8