辽宁省大连市庄河市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 下列图形不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各组线段中,能构成三角形的是( )A、2、4、7 B、4、5、9 C、5、8、10 D、1、3、63. 已知一个多边形的内角和是540°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形4. 下列是最简分式的是( )A、 B、 C、 D、5. 若把x、y的值同时扩大为原来的2倍,则下列分式的值保持不变的是( )A、 B、 C、 D、6. 如图,中,AC的垂直平分线EF交AC、BC于点E、F,连接AF.若 , , 则周长为( )
2. 下列各组线段中,能构成三角形的是( )A、2、4、7 B、4、5、9 C、5、8、10 D、1、3、63. 已知一个多边形的内角和是540°,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形4. 下列是最简分式的是( )A、 B、 C、 D、5. 若把x、y的值同时扩大为原来的2倍,则下列分式的值保持不变的是( )A、 B、 C、 D、6. 如图,中,AC的垂直平分线EF交AC、BC于点E、F,连接AF.若 , , 则周长为( )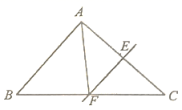 A、23 B、13 C、17 D、167. 若与的乘积中不含x的一次项,则m的值为( )A、-2 B、0 C、2 D、48. 若 , , 则代数式的值是( )A、-5 B、13 C、5 D、99. 如图所示,点E、F为网格中的格点,为等腰三角形,且点D是网格中的格点,则符合条件的三角形点D有( )
A、23 B、13 C、17 D、167. 若与的乘积中不含x的一次项,则m的值为( )A、-2 B、0 C、2 D、48. 若 , , 则代数式的值是( )A、-5 B、13 C、5 D、99. 如图所示,点E、F为网格中的格点,为等腰三角形,且点D是网格中的格点,则符合条件的三角形点D有( )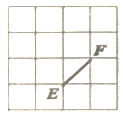 A、4个 B、6个 C、9个 D、10个10. 如图,中,若 , , , 若 , 则为( )
A、4个 B、6个 C、9个 D、10个10. 如图,中,若 , , , 若 , 则为( )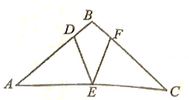 A、40° B、60° C、70° D、80°
A、40° B、60° C、70° D、80°二、填空题
-
11. 分解因式: .12. 若分式 的值为零,则x的值为 .
13. 若 , 则 .14. 如图,将一个等腰直角三角形及两个等边三角形按图摆放,若 , 则 .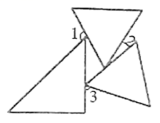 15. 如果是完全平方式,则 .16. 如图,四边形ABCD,BP、CP分别平分、 , 写出、、之间的数量关系 .
15. 如果是完全平方式,则 .16. 如图,四边形ABCD,BP、CP分别平分、 , 写出、、之间的数量关系 .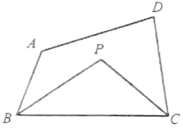
三、解答题
-
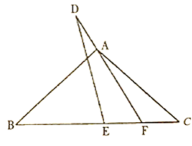
17. 计算:(1)、(2)、18. 解方程:(1)、(2)、19. 先化简,再求值: , 其中 .20. 如图,中,BE为AC边上的高,CD平分 , CD、BE相交于点F.若 , , 求的度数.
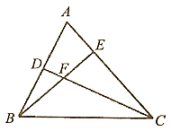 21. 如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证:BD=CE.
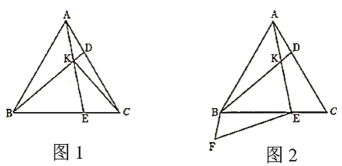
21. 如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,求证:BD=CE.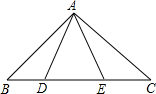 22. 冬季来临,某商场预购进一批毛衣.用9600元先购进一批毛衣,面市后因供不应求,商场决定又用16800元再次购进这批毛衣,所购数量是第一批购进量的2倍,但单价便宜了10元.该商场第一次购进这批毛衣的数量是多少?23.(1)、将图1中的甲图从中间按如图方式剪开,经过重新拼接变换到图乙,比较图甲与图乙,写出得到的公式:;
22. 冬季来临,某商场预购进一批毛衣.用9600元先购进一批毛衣,面市后因供不应求,商场决定又用16800元再次购进这批毛衣,所购数量是第一批购进量的2倍,但单价便宜了10元.该商场第一次购进这批毛衣的数量是多少?23.(1)、将图1中的甲图从中间按如图方式剪开,经过重新拼接变换到图乙,比较图甲与图乙,写出得到的公式:;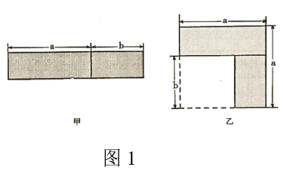 (2)、将图2中的甲图从中间按如图方式剪开,经过重新拼接变换到图乙,比较图甲与图乙,写出得到的公式:;
(2)、将图2中的甲图从中间按如图方式剪开,经过重新拼接变换到图乙,比较图甲与图乙,写出得到的公式:;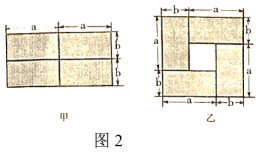 (3)、根据图1、图2中得到的公式,解决下列问题:
(3)、根据图1、图2中得到的公式,解决下列问题:①计算: ▲ ;
②若 , 求的值.
24. 在平面直角坐标系中,已知点、 , 点A关于x轴对称点为F,连接BF,作 , 连接DO交BF延长线于点C.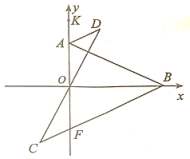 (1)、①直接写出点F的坐标 ▲ ;
(1)、①直接写出点F的坐标 ▲ ;②证明:≌;
(2)、动点P从F出发,以每秒1个单位长度的速度沿运动,到B点停止运动;动点Q从B出发,以每秒3个单位长度的速度沿 , 到F停止运动.二者同时开始运动,都要到达相应的终点才能停止运动.过点P作于点G,过点Q作于点H,问:当P点运动多少时间时,与全等?