辽宁省鞍山市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 使分式 $\frac{- 1}{x + 1}$ 有意义的x取值范围是（）

A、 $x > - 1$ B、 $x < - 1$ C、 $x \neq - 1$ D、 $x = - 1$

查看试题解析
2. 下面轴对称图形中对称轴最多的是（）

A、 B、 C、 D、

查看试题解析
3. 三根小木棒摆成一个三角形，其中两根木棒的长度分别是 $8 c m$ 和 $5 c m$ ，那么第三根小木棒的长度不可能是（）

A、 $5 c m$ B、 $8 c m$ C、 $10 c m$ D、 $13 c m$

查看试题解析
4. 下列运算正确的是（）

A、 $x^{5} + x^{5} = 2 x^{5}$ B、 $x^{5} \cdot x^{5} = 2 x^{10}$ C、 $x^{6} \div x^{2} = x^{3}$ D、 ${(^{})}^{3} = x^{27}$

查看试题解析
5. 如图，在下列条件中，不能证明△ABD≌△ACD的条件是（）

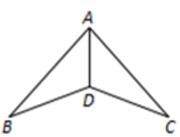A、BD＝DC，AB＝AC B、∠ADB＝∠ADC，BD＝DC C、∠B＝∠C，∠BAD＝∠CAD D、∠B＝∠C，BD＝DC

查看试题解析
6. 下列多项式能使用平方差公式进行因式分解的是（）

A、 $4 x^{2} + 1$ B、 $- m^{2} + 1$ C、 $- a^{2} - b^{2}$ D、 $2 x^{2} - y^{2}$

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ A = 105 °$ ， AC的垂直平分线MN交BC于点N，且 $A B + B N = B C$ ，则 $∠ B$ 的度数是（）

A、45° B、50° C、55° D、60°

查看试题解析
8. 下列各式计算正确的是（）

A、 ${(\frac{- 2^{} b}{3 c})}^{2} = \frac{4 a^{4} b^{2}}{3 c^{2}}$ B、 $\frac{1}{x} + \frac{1}{y} = \frac{1}{x + y}$ C、 $3 x y \div \frac{2 y^{2}}{3 x} = 2 y^{3}$ D、 $\frac{1 - a}{a^{2} - 2 a + 1} = \frac{1}{1 - a}$

查看试题解析
9. 近几年鞍山市的城市绿化率逐年增加，其中2019年，2020年，2021年鞍山的城市绿化面积分别是 $S_{1}$ ， $S_{2}$ ， $S_{3}$ ， 2021年与2020年相比，鞍山城市绿化的增长率提高（）

A、 $\frac{S_{3}}{S_{2}} - \frac{S_{2}}{S_{1}}$ B、 $\frac{S_{2} - S_{1}}{S_{3} - S_{2}}$ C、 $\frac{S_{3} - S_{2}}{S_{2}} - \frac{S_{2} - S_{1}}{S_{1}}$ D、 $\frac{S_{3} - S_{2}}{S_{3}} - \frac{S_{2} - S_{1}}{S_{2}}$

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 30 °$ ， BD平分 $∠ A B C$ 交AC于点D，过点D作 $D E ⊥ A B$ ，垂足为E，则各线段之间的关系：① $D E = C D$ ；② $A E = B E$ ；③ $A D = 2 C D$ ；其中正确的有（）

A、①②③ B、①② C、①③ D、②③

查看试题解析

二、填空题

11. 计算： $π^{0} + {(- 2)}^{- 2} =$ ．

查看试题解析
12. 一种细胞的直径是0.0000705m，用科学记数法可表示为m．

查看试题解析
13. 七边形内角和的度数是．

查看试题解析
14. 如图，从A处观测C处的仰角是 $∠ C A D = 36 °$ ，从B处观测C处的仰角 $∠ C B D = 74 °$ ，则从C处观测A，B两处的视角 $∠ B C A$ 的度数是．

查看试题解析
15. 如图，在 $△ ABC$ 中，点A的坐标为 $(0 ， 1)$ ，点B的坐标为 $(0 ， 4)$ ，点C的坐标为 $(4 ， 3)$ ，点D在第二象限，且 $△ ABD$ 与 $△ ABC$ 全等，点D的坐标是.

查看试题解析
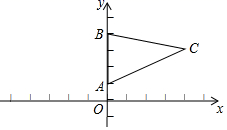16. 已知 $4 x^{2} + k x y + 9 y^{2}$ 是一个完全平方式，则 $k$ 的值是．

查看试题解析
17. 观察下列因式分解中的规律：① $x^{2} + 3 x + 2 = (x + 1) (x + 2)$ ；② $x^{2} + 7 x + 10 = (x + 2) (x + 5)$ ；③ $x^{2} - 5 x + 6 = (x - 2) (x - 3)$ ；④ $x^{2} - 2 x - 8 = (x + 2) (x - 4)$ ；利用上述系数特点分解因式 $x^{2} + x - 6 =$ ．

查看试题解析

三、解答题

18. 若三角形的底边为2m+1，高为2m，则此三角形的面积为.

查看试题解析
19. 按照要求进行计算：

(1)、计算： $[x (x^{2} y^{2} - x y) - (x y^{2} - y) (x^{2} - x y)] \div 3 x y^{2}$

(2)、利用乘法公式进行计算： $(2 x + y + z) (2 x - y - z)$

查看试题解析
20. 先化简，再求值， $\frac{x^{2} - 4 x + 4}{x^{2} - 4} \div \frac{x^{2} - 2 x}{x + 2} - 1$ ，其中 $x = - \frac{16}{5}$

查看试题解析
21. 如图，AC与BD交于点O， $A D = C B$ ， E、F是BD上两点，且 $A E = C F$ ， $D E = B F$ ．证明：

(1)、 $∠ D = ∠ B$ ；

(2)、AC与BD互相平分．

查看试题解析
22. 如图，P为 $∠ A O B$ 内一定点，M、N分别是射线OA、OB上的点，

(1)、当 $△ P M N$ 周长最小时，在图中画出 $△ P M N$ （保留作图痕迹）；

(2)、在（1）的条件下，已知 $∠ M P N = 110 °$ ，求 $∠ A O B$ 的度数．

查看试题解析
23. 2022年元旦及春节来临之际，我市对城市亮化工程招标，按照甲、乙两个工程队的投标书，甲、乙两队施工一天的工程费分别为1.5万元和1.2万元，根据甲乙两队的投标书测算，应有三种施工方案：
①甲队单独做这项工程刚好如期完成．②乙队单独做这项工程，要比规定日期多3天完成．③若甲、乙两队合作2天后，余下的工程由乙队单独做，也正好如期完成．

(1)、求规定如期完成的天数．

(2)、在确保如期完成的情况下，你认为以上三种方案哪种方案最节省工程款；通过计算说明理由．

查看试题解析
24. 如图，在平面直角坐标系中，点B的坐标是 $(0 ， - 4)$ ，点C的坐标为 $(- 6 ， 4)$ ， CB交x轴负半轴于点A，过点B作射线 $B M ⊥ B C$ ，作射线CD交BM于点D，且 $∠ B C D = 45 °$

(1)、求证：点A为线段BC的中点．

(2)、求点D的坐标．

查看试题解析
25. 如图，等边三角形ABC中，过点C作射线 $C M ⊥ B C$ ，点D是CM上的动点，以CD为边作等边三角形CDE，连结BE并延长交射线AD于点F

(1)、判断DE与AC的位置关系，并证明你的结论：

(2)、求 $∠ A F E$ 的度数；

(3)、在点D变化过程中，当线段BF的长度最大时，直接写出线段BF与CD的比值．

查看试题解析