江西省萍乡市2020-2021学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下面四组数据中，不能作为直角三角形的三边长是（）

A、6、8、10 B、7、24、25 C、2、5、7 D、9、12、15

查看试题解析
2. 下列计算，正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{(- 2) \times (- 2)} = 2$ C、 $3 \sqrt{2} - \sqrt{2} = 3$ D、 $\sqrt{8} + \sqrt{2} = \sqrt{10}$

查看试题解析
3. 下列四个命题是真命题的有（）
①同位角相等；
②相等的角是对顶角；
③直角三角形两个锐角互余；
④三个内角相等的三角形是等边三角形．

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 估算 $\sqrt{31} - 2$ 的值（）

A、在 $1$ 和 $2$ 之间 B、在 $2$ 和 $3$ 之间 C、在 $3$ 和 $4$ 之间 D、在 $4$ 和 $5$ 之间

查看试题解析
5. 已知点M(2，﹣3)，点N与点M关于x轴对称，则点N的坐标是（）

A、(﹣2，3) B、(﹣2，﹣3) C、(3，2) D、(2，3)

查看试题解析
6. 如图，网格中每个小正方形的边长均为1，点A，B，C都在格点上，以A为圆心，AB为半径画弧，交最上方的网格线于点D，则CD的长为（）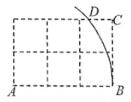

A、 $\sqrt{5}$ B、0.8 C、 $3 - \sqrt{5}$ D、 $\sqrt{13}$

查看试题解析
7. 如图，直线l₁ $∥$ l₂ ，被直线l₃、l₄所截，并且l₃⊥l₄ ， ∠1＝46°，则∠2等于（）

A、56° B、34° C、44° D、46°

查看试题解析
8. 某校随机抽查了10名学生的体育成绩，得到的结果如表：
成绩（分）
46
47
48
49
50
人数（人）
1
2
3
2
2
下列说法正确的是（）

A、这10名同学的体育成绩的方差为50 B、这10名同学的体育成绩的众数为50分 C、这10名同学的体育成绩的中位数为48分 D、这10名同学的体育成绩的平均数为48分

查看试题解析
9. 已知 ${\begin{array}{l} x = 2, \\ y = 1 \end{array}$ 是二元一次方程组 ${\begin{array}{l} a x + b y = 7, \\ a x - b y = 1 \end{array}$ 的解，则 $a - b$ 的值为（）

A、－1 B、1 C、2 D、3

查看试题解析
10. 如图，一次函数y₁＝ax+b和y₂＝bx+a在同一平面直角坐标系中的图象可能的是（）

A、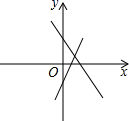 B、 C、 D、

查看试题解析

二、填空题

11. $\sqrt{9}$ 的平方根是

查看试题解析
12. 把直线y=2x﹣1向上平移2个单位，所得直线的解析式是

查看试题解析
13. 将一张面值50元的人民币，兑换成5元或10元的零钱，两种人民币都要有，那么共有种兑换方案．

查看试题解析
14. 如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=15°，那么∠2的度数是

查看试题解析
15.
我国古代有这样一道数学问题：“枯木一根直立地上，高二丈，周三尺，有葛藤自根缠绕而上，五周而达其顶，问葛藤之长几何？”题意是：如图所示，把枯木看作一个圆柱体，因一丈是十尺，则该圆柱的高为20尺，底面周长为3尺，有葛藤自点A处缠绕而上，绕五周后其末端恰好到达点B处，则问题中葛藤的最短长度是尺．

查看试题解析
16. 面试时，某人的基本知识、表达能力、工作态度的成绩分别是90分、80分、85分，若依次按20%、40%、40%的比例确定成绩，则这个人的面试成绩是．

查看试题解析
17. 如图，已知∠A＝60°，∠B＝20°，∠C＝30°，则∠BDC的度数为．

查看试题解析
18. 如图，在平面直角坐标系xOy中，三角板的直角顶点P的坐标为(2，2)，一条直角边与x轴的正半轴交于点A，另一直角边与y轴交于点B，三角板绕点P在坐标平面内转动的过程中，当△POA为等腰三角形时，请写出所有满足条件的点B的坐标．

查看试题解析

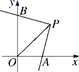
三、解答题

19.

(1)、化简： $(\sqrt{6} - 2 \sqrt{15}) \times \sqrt{3} - 6 \sqrt{\frac{1}{2}}$ ；

(2)、解方程组： ${\begin{array}{l} 2 (x + 1) - y = 6 \\ x = y - 1 \end{array}$ ．

查看试题解析
20. 如图，已知DE∥BC，BE是∠ABC的平分线，∠C=70°，∠ABC=50°．求∠DEB和∠BEC的度数．

查看试题解析
21. 宣传交通安全知识，争做安全小卫士.某校进行“交通安全知识”宣传培训后进行了一次测试.学生考分按标准划分为不合格、合格、良好、优秀四个等级，为了解全校的考试情况，对在校的学生随机抽样调查，得到图（1）的条形统计图，请结合统计图回答下列问题：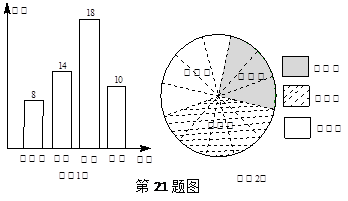

(1)、该校抽样调查的学生人数为名；抽样中考生分数的中位数所在等级是；

(2)、抽样中不及格的人数是多少？占被调查人数的百分比是多少？

(3)、若已知该校九年级有学生500名，图（2）是各年级人数占全校人数百分比的扇形图（图中圆心角被等分），请你估计全校优良（良好与优秀）的人数约有多少人？

查看试题解析
22. 一次函数CD： $y = - k x + b$ 与一次函数AB： $y = 2 k x + 2 b$ ，都经过点B（-1，4）.

(1)、求两条直线的解析式；

(2)、求四边形ABDO的面积.

查看试题解析
23. 红太阳大酒店客房部有三人间、双人间和单人间客房，收费数据如下表（例如三人间普通间客房每人每天收费50元）．为吸引客源，在五一黄金周期间进行优惠大酬宾，凡团体入住一律五折优惠．一个50人的旅游团在五月二号到该酒店住宿，租住了一些三人间、双人间普通客房，并且每个客房正好住满，一天一共花去住宿费1510元．

普通间（元/人/天）
豪华间（元/人/天）
贵宾间（元/人/天）
三人间
50
100
500
双人间
70
150
800
单人间
100
200
1500

(1)、三人间、双人间普通客房各住了多少间？

(2)、设三人间共住了x人，则双人间住了 ▲ 人，一天一共花去住宿费用y元表示，写出y与x的函数关系式；

(3)、在直角坐标系内画出这个函数图象；

(4)、如果你作为旅游团团长，你认为上面这种住宿方式是不是费用最少？为什么？

查看试题解析
24. 平面内的两条直线有相交和平行两种位置关系.

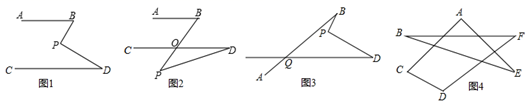(1)、如图1，若 $A B / / C D$ ，点 $P$ 在 $A B$ 、 $C D$ 内部， $∠ B = 50 °$ ， $∠ D = 30 °$ ，求 $∠ B P D$ 的度数.

(2)、如图2，在AB∥CD的前提下，将点 $P$ 移到 $A B$ 、 $C D$ 外部，则 $∠ B P D$ 、 $∠ B$ 、 $∠ D$ 之间有何数量关系？请证明你的结论.

(3)、如图3，写出 $∠ B P D$ 、 $∠ B$ 、 $∠ D$ 、 $∠ B Q D$ 之间的数量关系？(不需证明)

(4)、如图4，求出 $∠ A + ∠ B + ∠ C + ∠ D + ∠ E + ∠ F$ 的度数.

查看试题解析
25. 如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．

(1)、实验与探究：
观察图，易知A(0，2)关于直线l的对称点 $A$ 的坐标为(2，0)，请在图中分别标明B(5，3)、C(﹣2，5)关于直线l的对称点 $B$ 、 $C$ 的位置，并写出他们的坐标： $B$ ， $C$ ；

(2)、归纳与发现：结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a，b)关于第一、三象限的角平分线l的对称点 $P$ 的坐标为（不必证明）；

(3)、运用与拓广：已知两点D(1，﹣3)、E(﹣3，﹣4)，试在直线l上确定一点Q，使点Q到D、E两点的距离之和最小．

查看试题解析

	普通间（元/人/天）	豪华间（元/人/天）	贵宾间（元/人/天）
三人间	50	100	500
双人间	70	150	800
单人间	100	200	1500

成绩（分）	46	47	48	49	50
人数（人）	1	2	3	2	2