吉林省吉林市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，北京2022年冬奥会会徽，是将蒙汉两种文字的“冬”字融为一体而成．组成会徽的四个图案中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列运算一定正确的是（）

A、 $(3 a)^{3} = 9 a^{3}$ B、 $a^{2} \cdot a^{- 1} = a^{- 2}$ C、 $π^{0} = 1$ D、 ${(\frac{1}{2})}^{- 2} = - 4$

查看试题解析
3. 如图， $A B$ 和 $C D$ 相交于点O，则下列结论错误的是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 1 = ∠ B$ C、 $∠ 2 > ∠ D$ D、 $∠ A + ∠ D = ∠ B + ∠ C$

查看试题解析
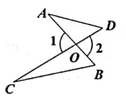4. 在△ABC和△ $A B C$ 中，AB= $A B$ ， ∠B=∠ $B$ ，补充条件后仍不一定能保证△ABC≌△ $A B C$ ，则补充的这个条件是（）

A、 $B C$ = $B^{^{'}} C^{^{'}}$ B、 $∠ A$ =∠ $A$ C、 $A C$ = $A C$ D、 $∠ C$ =∠ $C$

查看试题解析
5. 一个三角形三个内角的度数分别是x，y，z．若 $| x - y | + (x + y - z)^{2} = 0$ ，则这个三角形是（）

A、等腰三角形 B、等边三角形 C、等腰直角三角形 D、不存在

查看试题解析
6. 甲车行驶30千米与乙车行驶40千米所用时间相同，已知乙车每小时比甲车多行驶15千米，设甲车的速度为x千米/小时，依据题意列方程正确的是（）

A、 $\frac{30}{x} = \frac{40}{x - 15}$ B、 $\frac{30}{x - 15} = \frac{40}{x}$ C、 $\frac{30}{x} = \frac{40}{x + 15}$ D、 $\frac{30}{x + 15} = \frac{40}{x}$

查看试题解析

二、填空题

7. 新型冠状病毒的直径约为 $0.0000001 m$ ，数0.0000001用科学记数法表示为．

查看试题解析
8. 点 $P (- 2 ， 5)$ 关于x轴对称的点的坐标为．

查看试题解析
9. 因式分解： $m^{3} - m =$ ．

查看试题解析
10. 若一个多边形的每一个外角都等于40°，则这个多边形的边数是．

查看试题解析
11. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则x的值等于．

查看试题解析
12. 在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $∠ C = 30 °$ ．用无刻度的直尺和圆规在 $B C$ 边上找一点D，使 $△ A C D$ 为等腰三角形．下列作法正确的有个．

查看试题解析
13. 如图，在 $△ A B C$ 中， $A B = 5$ ， $A C = 7$ ． $M N$ 为 $B C$ 边上的垂直平分线，若点D在直线 $M N$ 上，连接 $A D$ ， $B D$ ，则 $△ A B D$ 周长的最小值为．

查看试题解析
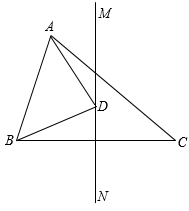14. 如图，王老师把家里的 $W I F I$ 密码设置成了数学问题．吴同学来王老师家做客，看到 $W I F I$ 图片，思索了一会儿，输入密码，顺利地连接到了王老师家里的网络，那么她输入的密码是．
账号：Mr．Wang's house
王 $\oplus ⌊ x^{13} y z^{4} ⌋ = w a n g 1314$
浩 $\oplus ⌊ x y^{15} \cdot x^{2} z^{20} ⌋ = h a o 31520$
阳 $\oplus ⌊ {(^{} y)}^{4} \cdot {({^{}}^{})}^{2} ⌋ =$ 密码

查看试题解析

三、解答题

15. 计算： $(x + 1) (x - 4) - (x - 1)^{2}$ ．

查看试题解析
16. $\frac{1}{x - 5}$ ＝ $\frac{10}{x^{2} - 25}$ ．

查看试题解析
17. 如图，把 $R_{1} ， R_{2} ， R_{3}$ 三个电阻串联起来，线路 $A B$ 上的电流为I，电压为U，则 $U = I R_{1} + I R_{2} + I R_{3}$ ．当 $R_{1} = 19.7 ， R_{2} = 32.4 ， R_{3} = 35.9 ， I = 2.5$ 时，求U的值．

查看试题解析
18. 如图，点B，E，C，F在一条直线上， $A B = D E$ ， $∠ A B C = ∠ D E F$ ， $B E = C F$ ．求证 $∠ A = ∠ D$ ．

查看试题解析
19. 先化简 $(1 - \frac{1}{a}) \div \frac{a^{2} - 1}{a^{2} + 2 a + 1}$ ，再从 $- 1$ ， 0，1，2中选择一个合适的数作为a的值代入求值．

查看试题解析
20. 某工厂生产A，B两种型号的扫地机器人．B型机器人比A型机器人每小时的清扫面积多50%，清扫 $100 m^{2}$ 所用的时间，A型机器人比B型机器人多用40分钟．求A型号扫地机器人每小时清扫面积是多少？

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ B = 75 °$ ， $∠ C = 35 °$ ． $A E ⊥ B C$ 于点E， $A D$ 平分 $∠ B A C$ ．

(1)、求证 $A D = C D$ ；

(2)、求 $∠ E A D$ 的度数．

查看试题解析
22. 如图1，有甲、乙、丙三种纸片，其中甲是边长为a的正方形，乙是长为a，宽为b的长方形，丙是边长为b的正方形（ $a > b$ ）．

(1)、如图2，用甲、丙纸片各1张，乙纸片2张，可以紧密拼接成一个大正方形，请根据图形的面积写出一个乘法公式；

(2)、若要用这三种纸片紧密拼接成一个边长为 $(2 a + b)$ 大正方形，则需要取甲、乙、丙纸片各多少张．

查看试题解析
23. 如图， $4 \times 4$ 正方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长均为1，点A，B都在格点上，按下列要求作图，使得所画图形的顶点均在格点上．

(1)、在图1中画一个以线段 $A B$ 为边的轴对称 $△ A B C$ ，使其面积为2；

(2)、在图2中画一个以线段 $A B$ 为边的轴对称四边形 $A B D E$ ，使其面积为6．

查看试题解析
24. 角的平分线的判定定理：角的内部到角的两边的距离相等的点在角的平分线上．
小强证明该定理的步骤如下：
已知：如图1，点P在 $O C$ 上， $P D ⊥ O A$ 于点D， $P E ⊥ O B$ 于点E，且 $P D = P E$ ．
求证： $O C$ 是 $∠ A O B$ 的平分线．
证明：通过测量可得 $∠ A O C = 23 °$ ， $∠ B O C = 23 °$ ．
∴ $∠ A O C = ∠ B O C$ ． ∴ $O C$ 是 $∠ A O B$ 的平分线．

(1)、关于定理的证明，下面说法正确的是（）

A、小强用到了从特殊到一般的方法证明该定理． B、只要测量一百个到角的两边的距离相等的点都在角的平分线上，就能证明该定理． C、不能只用这个角，还需要用其它角度进行测量验证，该定理的证明才完整． D、小强的方法可以用作猜想，但不属于严谨的推理证明．

(2)、利用小强的已知和求证，请你证明该定理；

(3)、如图2，在五边形 $A B C D E$ 中， $B C = C D = D E$ ， $∠ A B C = 80 °$ ， $∠ B A E = 110 °$ ， $∠ A E D = 100 °$ ，在五边形 $A B C D E$ 内有一点F，使得 $S_{△ B C F} = S_{△ C D F} = S_{△ D E F}$ ．直接写出 $∠ C F D$ 的度数．

查看试题解析

25. （教材呈现）人教版八年级上册数学教材第112页的第7题：

已知 $a + b = 5$ ， $a b = 3$ ，求 $a^{2} + b^{2}$ 的值．

（例题讲解）老师讲解了这道题的两种方法：

方法一

方法二

∵ $a + b = 5$ ，

∴ $(a + b)^{2} = 25$ ．

∴ $a^{2} + 2 a b + b^{2} = 25$ ．

∵ $a b = 3$ ，

∴ $a^{2} + b^{2} = 25 - 2 a b = 25 - 6 = 19$ ．

∵ $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ ，

∵ $a^{2} + b^{2} = (a + b)^{2} - 2 a b$ ，

∵ $a + b = 5$ ， $a b = 3$ ，

∴ $a^{2} + b^{2} = 25 - 6 = 19$ ．

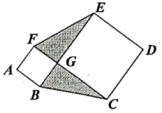(1)、（方法运用）请你参照上面两种解法，解答以下问题．

已知 $a - b = 1$ ， $a^{2} + b^{2} = 9$ ，求 $a b$ 的值；

(2)、已知

a + \frac{1}{a} = 4

，求

{(a - \frac{1}{a})}^{2}

的值．

(3)、（拓展提升）

如图，在六边形 $A B C D E F$ 中，对角线 $B E$ 和 $C F$ 相交于点G，当四边形 $A B G F$ 和四边形CDEG都为正方形时，若 $B E = 8$ ，正方形 $A B G F$ 和正方形CDEG的面积和为36，直接写出阴影部分的面积．

查看试题解析

26. 如图， $△ A B C$ 是边长为 $6 c m$ 的等边三角形，点P，Q分别从顶点A，B同时出发，点P沿射线 $A B$ 运动，点Q沿折线 $B C - C A$ 运动，且它们的速度都为 $1 c m / s$ ．当点Q到达点A时，点P随之停止运动连接 $P Q$ ， $P C$ ，设点P的运动时间为 $t (s)$ ．

(1)、当点Q在线段 $B C$ 上运动时， $B Q$ 的长为（ $c m$ ）， $B P$ 的长为（ $c m$ ）（用含t的式子表示）；

(2)、当 $P Q$ 与 $△ A B C$ 的一条边垂直时，求t的值；

(3)、在运动过程中，当 $△ C P Q$ 是等腰三角形时，直接写出t的值．

查看试题解析