河北省承德市宽城县2021-2022学年八年级上学期期末考试数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下面有4个汽车标志图案，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各式是最简二次根式的是（）

A、 $\sqrt{13}$ B、 $\sqrt{12}$ C、 $\sqrt{3^{2}}$ D、 $\sqrt{\frac{2}{3}}$

查看试题解析
3. 计算 $\frac{x}{{(x + 1)}^{2}} + \frac{1}{{(x + 1)}^{2}}$ 的结果是（）

A、 $\frac{1}{x + 1}$ B、 $\frac{1}{{(x + 1)}^{2}}$ C、1 D、 $x + 1$

查看试题解析
4. 下列等式成立的是（）

A、 $3 + 4 \sqrt{2} = 7 \sqrt{2}$ B、 $\sqrt{3} \times \sqrt{2} = \sqrt{5}$ C、 $\sqrt{3} \div \frac{1}{\sqrt{6}} = 2 \sqrt{3}$ D、 $\sqrt{{(- 3)}^{2}} = 3$

查看试题解析
5. 如图，数轴上点A对应的数是0，点B对应的数是1，BC⊥AB，垂足为B，且BC=2，以A为圆心，AC为半径画弧，交数轴于点D，则点D表示的数为（）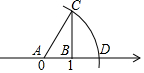

A、 $2.2$ B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
6. 如图，AC⊥BE于点C，DF⊥BE于点F，BC＝EF，如果添加一个条件后，可以直接利用“HL”来证明△ABC≌△DEF，则这个条件应该是（）

A、AC=DE B、∠D=∠A C、AB=DE D、∠B=∠E

查看试题解析
7. 若 $a \neq b$ ，则下列分式化简正确的是（）

A、 $\frac{a + 2}{b + 2} = \frac{a}{b}$ B、 $\frac{a - 2}{b - 2} = \frac{a}{b}$ C、 $\frac{a^{2}}{b^{2}} = \frac{a}{b}$ D、 $\frac{\frac{1}{2} a}{\frac{1}{2} b} = \frac{a}{b}$

查看试题解析
8. 计算 $\frac{1}{\sqrt{2} - 1}$ 的结果是（）

A、 $\sqrt{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2} - 1$ D、 $\sqrt{2} + 1$

查看试题解析
9. 如图1，已知 $∠ A B C$ ，用尺规作它的角平分线．
如图2，步骤如下，

第一步：以B为圆心，以a为半径画弧，分别交射线 BA ， BC 于点D，E；

第二步：分别以D，E为圆心，以b为半径画弧，两弧在 $∠ A B C$ 内部交于点P；

第三步：画射线 BP ．射线 BP 即为所求．

下列正确的是（）

A、a，b均无限制 B、 $a > 0$ ， $b > \frac{1}{2} D E$ 的长 C、a有最小限制，b无限制 D、 $a \geq 0$ ， $b < \frac{1}{2} D E$ 的长

查看试题解析
10. 对于二次根式的性质 $\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$ 中，关于a、b的取值正确的说法是（）

A、a≥0，b≥0 B、a≥0，b＞0 C、a≤0，b≤0 D、a≤0，b＜0

查看试题解析
11. 如图，长为 $8 c m$ 的橡皮筋放置在数轴上，固定两端A和B，然后把中点C垂直向上拉升 $3 c m$ 到D点，则橡皮筋被拉长了（）

A、 $2 c m$ B、 $3 c m$ C、 $4 c m$ D、 $1 c m$

查看试题解析
12. 某化肥厂计划在规定日期内生产化肥120吨，由于采用了新技术，每天多生产化肥3吨，实际生产180吨与原计划生产120吨的时间相等．设原计划每天生产x吨化肥，那么适合x的方程是（）

A、 $\frac{120}{x + 3}$ = $\frac{180}{x}$ B、 $\frac{120}{x - 3} = \frac{180}{x}$ C、 $\frac{120}{x} = \frac{180}{x + 3}$ D、 $\frac{120}{x} = \frac{80}{x - 3}$

查看试题解析
13. 满足下列条件的两个三角形不一定全等的是（）

A、周长相等的两个三角形 B、有一腰和底边对应相等的两个等腰三角形 C、三边都对应相等的两个三角形 D、两条直角边对应相等的两个直角三角形

查看试题解析
14. 关于x的分式方程 $\frac{5}{x} = \frac{a}{x - 2}$ 有解，则字母a的取值范围是（）

A、 $a = 2$ 或 $a = 0$ B、 $a \neq 0$ C、 $a \neq 5$ D、 $a \neq 5$ 且 $a \neq 0$

查看试题解析
15. 数轴上表示1， $\sqrt{2}$ 的对应点分别为A，B，点B关于点A的对称点为C，则点C所表示的数是（）

A、 $\sqrt{2} - 1$ B、 $1 - \sqrt{2}$ C、 $2 - \sqrt{2}$ D、 $\sqrt{2} - 2$

查看试题解析
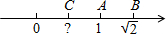16. 如图，在Rt $△$ ABC中，∠B＝90°，AB＝3，BC＝4，将 $△$ ABC折叠，使点B恰好落在边AC上，与点 $B$ 重合，AE为折痕，则E $B$ 长为（）

A、3cm B、2.5cm C、1.5cm D、1cm

查看试题解析

二、填空题

17. 若- $\sqrt{{(x - 2)}^{2}} = 2 - x$ ，则 $x$ 的取值范围是.

查看试题解析
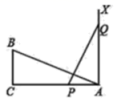
18. 如图，在 $R t △ A B C$ 中， $∠ C = 90 ° ， A C = 12 c m ， B C = 6 c m$ ，一条线段 $P Q = A B$ ， P，Q两点分别在线段 $A C$ 和 $A C$ 的垂线 $A X$ 上移动，若以A、B、C为顶点的三角形与以A、P、Q为顶点的三角形全等，则 $A P$ 的长为．

查看试题解析
19. 如图，在 $△ A B C$ 中， $B A = B C$ ， $B H$ 平分 $∠ A B C$ ，点P，D分别是 $B H$ 和 $A B$ 上的任意一点，连接 $C D$ ，设 $△ A C D$ 的面积为 $n$ ， $P A + P D = m$ ．

(1)、当点P，H重合时， $S_{△ A P D} =$ ．

(2)、连接 $C D$ 交 $B H$ 于点E，则m $C D$ （填“ $>$ ”，“ $<$ ”，“ $=$ ”，“ $\geq$ ”或“ $\leq$ ”）；

查看试题解析

三、解答题

20. 先化简，再求值： $(1 - \frac{1}{a - 2}) \div \frac{a - 3}{a^{2} - 4}$ ，其中 $a = - 3$ ．

查看试题解析
21. 王涵想复习分式方程，由于印刷问题，有一个数“？”看不清楚： $\frac{x}{x - 3} = 2 - \frac{?}{x - 3}$

(1)、她把这个数“ $?$ ”猜成 $- 2$ ，请你帮王涵解这个分式方程；

(2)、王涵的妈妈说：“我看到标准答案是： $x = 3$ 是方程的增根，原分式方程无解”，请你求出原分式方程中“？”代表的数是多少？

查看试题解析
22. 如图，已知 $A B = 4$ ， $A C = 7$ ．

(1)、用尺规作 $B C$ 边的垂直平分线；（保留作图痕迹，不写作法）

(2)、若 $B C$ 边的垂直平分线交 $A C$ 于D、交 $B C$ 于E；
①连接 $B D$ ，求 $△ A B D$ 的周长；

②若 $∠ A D B = 52 °$ ，求 $∠ D B C$ 的度数．

查看试题解析
23.

(1)、计算： $(\sqrt{5} - \sqrt{3}) (\sqrt{5} + \sqrt{3}) + 1$ ；

(2)、计算： $\sqrt{125} + 9 \sqrt{\frac{2}{27}} - \frac{1}{2} \sqrt{24} + {(\sqrt{5})}^{2}$ ；

(3)、下面是甜甜同学进行实数运算的过程，认真阅读并完成相应的任务：
$\sqrt{\frac{9}{2}} - \sqrt{12} \times (\sqrt{24} + 3 \sqrt{\frac{2}{3}})$

$= \frac{\sqrt{9}}{\sqrt{2}} - \sqrt{12} \times (\sqrt{24} + 3 \sqrt{\frac{2}{3}})$ ……第一步

$= \frac{3 \sqrt{2}}{2} - 2 \sqrt{3} \times 2 \sqrt{6} + 2 \times 3 \sqrt{3} \times \sqrt{\frac{2}{3}}$ ……第二步

$= \frac{3 \sqrt{2}}{2} - 12 \sqrt{2} + 6 \sqrt{2}$ ……第三步

$= - \frac{9 \sqrt{2}}{2}$ ……第四步

任务一：以上化简步骤中第一步化简的依据是：；

任务二：第步开始出现错误，请写出错误的原因，该试运算正确结果是．

查看试题解析
24. 如图，已知在 $Δ A B C$ 和 $Δ D C B$ 中， $∠ A = ∠ D = 90 °$ ， $A B = C D$ ， $A C$ 与 $B D$ 交于点 $E$ ，过点 $E$ 作 $E F ⊥ B C$ 于点 $F$ .

(1)、求证： $A C = B D$ ；

(2)、求证： $E F$ 垂直平分 $B C$ ；

(3)、若 $E F = D E$ ，求 $∠ A B E$ 的度数.

查看试题解析
25. 某单位在疫情期间用6000元购进A、B两种口罩1100包，购买A种口罩与购买B种口罩的费用相同，且一包A种口罩的单价是一包B种口罩单价的1.2倍．

(1)、求A，B两种口罩一包的单价各是多少元？

(2)、若计划用不超过11000元的资金再次购进A、B两种口罩共2000包，已知A、B两种口罩的进价不变，求A种口罩最多能购进多少包？

查看试题解析
26. 在 $△ A B C$ 中， $A B = A C ， B C = 8$ ，点M从点B出发沿射线 $B A$ 移动，同时点N从点C出发沿线段 $A C$ 的延长线移动，点M，N移动的速度相同， $M N$ 与 $B C$ 相交于点D．

(1)、如图1，过点M作 $M E / / A C$ ，交 $B C$ 于点E；
①图中与 $B M$ 相等的线段 ▲ 、 ▲ ；
②求证： $△ D M E ≌ △ D N C$ ；

(2)、如图2，若 $∠ A = 60 °$ ，当点M移动到 $A B$ 的中点时，求 $C D$ 的长度；

(3)、如图3，过点M作 $M F ⊥ B C$ 于点F，在点M从点B向点A（点M不与点A，B重合）移动的过程中，线段 $B F$ 与 $C D$ 的和是否保持不变？若保持不变，请直接写出 $B F$ 与 $C D$ 的长度和；若改变，请说明理由．

查看试题解析