河北省承德市承德县2021-2022学年八年级上学期期末考试数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 第24届冬奥会将于2022年2月4日-2月20日在北京和张家口举办.下列四个图分别是四届冬奥会图标中的一部分,共中是轴对称图形的为( )A、
 B、
B、 C、
C、 D、
D、 2. 承德市2021年前三季度主要经济指标保持稳定增长,各项民生保障政策落地落实,全市城镇新增就业人数约4.26万人,城镇登记失业率为3.86%.其中近似数4.26万是精确到( )A、万位 B、千位 C、百位 D、百分位3. 可以表示( )A、0.2的平方根 B、的算术平方根 C、0.2的负的平方根 D、的立方根4. 在△ABC中,点D在边BC上,若AD2+BD2=AB2 , 则下列结论正确的是( )A、∠BAC=90° B、∠BAD=90° C、∠ABD=90° D、∠ADB=90°5. 若 , 则下列分式化简正确的是( )A、 B、 C、 D、6. 如图是作 的作图痕迹,则此作图的已知条件是( )
2. 承德市2021年前三季度主要经济指标保持稳定增长,各项民生保障政策落地落实,全市城镇新增就业人数约4.26万人,城镇登记失业率为3.86%.其中近似数4.26万是精确到( )A、万位 B、千位 C、百位 D、百分位3. 可以表示( )A、0.2的平方根 B、的算术平方根 C、0.2的负的平方根 D、的立方根4. 在△ABC中,点D在边BC上,若AD2+BD2=AB2 , 则下列结论正确的是( )A、∠BAC=90° B、∠BAD=90° C、∠ABD=90° D、∠ADB=90°5. 若 , 则下列分式化简正确的是( )A、 B、 C、 D、6. 如图是作 的作图痕迹,则此作图的已知条件是( )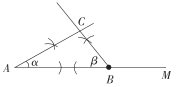 A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角7. 下列二次根式化为最简二次根式后能与合并的是( )A、 B、 C、 D、8. 如图,已知△ABC与△BDE全等,其中点D在边AB上,AB>BC,BD=CA,DE∥AC,BC与DE交于点F,下列与AD+AC相等的是( )
A、已知两边及夹角 B、已知三边 C、已知两角及夹边 D、已知两边及一边对角7. 下列二次根式化为最简二次根式后能与合并的是( )A、 B、 C、 D、8. 如图,已知△ABC与△BDE全等,其中点D在边AB上,AB>BC,BD=CA,DE∥AC,BC与DE交于点F,下列与AD+AC相等的是( )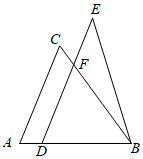 A、DE B、BE C、BF D、DF9. 若要运用反证法证明“若 , 则”,首先应该假设( )A、 B、 C、 D、10. 下列计算正确的是( )A、 B、 C、 D、11. 如图,直线AB,CD交于点O,若AB,CD是等边△MNP的两条对称轴,且点P在直线CD上(不与点O重合),则点M,N中必有一个在( )
A、DE B、BE C、BF D、DF9. 若要运用反证法证明“若 , 则”,首先应该假设( )A、 B、 C、 D、10. 下列计算正确的是( )A、 B、 C、 D、11. 如图,直线AB,CD交于点O,若AB,CD是等边△MNP的两条对称轴,且点P在直线CD上(不与点O重合),则点M,N中必有一个在( )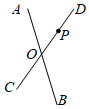 A、∠AOD的内部 B、∠BOD的内部 C、∠BOC的内部 D、直线AB上12. 已知两个不等于0的实数 、 满足 ,则 等于( )A、-2 B、-1 C、1 D、213. 如图1,在中, , , M是的中点,设 , 则表示实数a的点落在数轴上(如图2)所标四段中的( )
A、∠AOD的内部 B、∠BOD的内部 C、∠BOC的内部 D、直线AB上12. 已知两个不等于0的实数 、 满足 ,则 等于( )A、-2 B、-1 C、1 D、213. 如图1,在中, , , M是的中点,设 , 则表示实数a的点落在数轴上(如图2)所标四段中的( )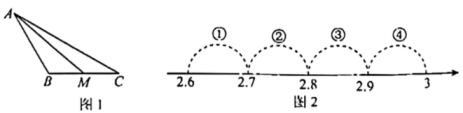 A、①段 B、②段 C、③段 D、④段14. 如图,在中, , 的垂直平分线交于点D,交于点E,连接 . 给出下列说法:①平分;②;③图中有四个等腰三角形;④当时,是等边三角形;⑤当时,可依据“HL”判定 . 其中正确的是( )
A、①段 B、②段 C、③段 D、④段14. 如图,在中, , 的垂直平分线交于点D,交于点E,连接 . 给出下列说法:①平分;②;③图中有四个等腰三角形;④当时,是等边三角形;⑤当时,可依据“HL”判定 . 其中正确的是( )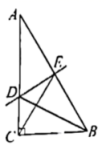 A、①②③ B、②③④ C、②③⑤ D、②④⑤
A、①②③ B、②③④ C、②③⑤ D、②④⑤二、填空题
-
15. 若分式 值为0,则 .16. “全等三角形的对应边相等”的逆命题是: .17. 如图,点A、B、C分别在边长为1的正方形网格图顶点,则 .
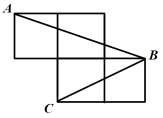 18. 如图,点A,B在直线的同侧,点A到的距离 , 点B到的距离 , 已知 , P是直线上的一个动点,记的最小值为a,的最大值为b.
18. 如图,点A,B在直线的同侧,点A到的距离 , 点B到的距离 , 已知 , P是直线上的一个动点,记的最小值为a,的最大值为b.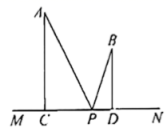 (1)、;(2)、 .
(1)、;(2)、 .三、解答题
-
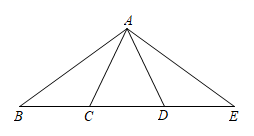
19. 计算:(1)、(2)、 .20. 先化简,再求值: , 其中x是6的平方根.21. 如图,点C、D在BE上,BC=ED,AC=AD,求证:AB=AE.
 22. 关于x的方程: - =1.(1)、当a=3时,求这个方程的解;(2)、若这个方程有增根,求a的值.23. 阅读下面的文字,解答问题.
22. 关于x的方程: - =1.(1)、当a=3时,求这个方程的解;(2)、若这个方程有增根,求a的值.23. 阅读下面的文字,解答问题.现规定:分别用和表示实数x的整数部分和小数部分,如实数3.14的整数部分是 , 小数部分是;实数的整数部分是 , 小数部分是无限不循环小数,无法写完整,但是把它的整数部分减去,就等于它的小数部分,即就是的小数部分,所以 .
(1)、 , ; , .(2)、如果 , , 求的立方根.24. 接种疫苗是阻断新冠病毒传播的有效途径,针对疫苗急需问题,某制药厂紧急批量生产,计划每天生产疫苗16万剂,但受某些因素影响,有10名工人不能按时到厂.为了应对疫情,回厂的工人加班生产,由原来每天工作8小时增加到10小时,每人每小时完成的工作量不变,这样每天只能生产疫苗15万剂.(1)、求该厂当前参加生产的工人有多少人?(2)、生产4天后,未到的工人同时到岗加入生产,每天生产时间仍为10小时.若上级分配给该厂共760万剂的生产任务,问该厂共需要多少天才能完成任务?