广东省珠海市香洲区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列几种著名的数学曲线中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 某种新冠病毒的直径为0.0000076cm，将数字0.0000076用科学记数法表示为（）

A、 $7.6 \times 10^{6}$ B、 $0.76 \times 10^{7}$ C、 $0.76 \times 10^{- 5}$ D、 $7.6 \times 10^{- 6}$

查看试题解析
3. 下列哪个度数不可能是一个多边形的内角和（）

A、 $360 °$ B、 $450 °$ C、 $900 °$ D、 $1800 °$

查看试题解析
4. 下列运算正确的是（）

A、a³+a³＝a⁶ B、（a³）²＝a⁶ C、（ab）²＝ab² D、2a•3a＝5a

查看试题解析
5. 已知三角形的两边长分别是3cm和7cm，则下列长度的线段中能作为第三边的是（）

A、3cm B、4cm C、7cm D、10cm

查看试题解析
6. 已知图中的两个三角形全等，则 $∠ 1$ 等于（）

A、 $70 °$ B、 $68 °$ C、 $58 °$ D、 $52 °$

查看试题解析
7. 如图，从边长为a的大正方形中剪掉一个边长为b的小正方形，将阴影部分沿虚线剪开，拼成右边的矩形.根据图形的变化过程写出的一个正确的等式是（）

A、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ B、 $a (a - b) = a^{2} - a b$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 $a^{2} - b^{2} = (a + b) (a - b)$

查看试题解析
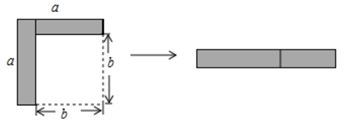8. 如图，在△ABC中，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧交于两点，过这两点作直线交AC于点E，交BC于点D，连接AD．若△ADB的周长为15，AE＝4，则△ABC的周长为（）

A、17 B、19 C、21 D、23

查看试题解析
9. 已知A= $2 x + 6$ ， B是多项式，在计算B-A时，小海同学把B-A错看成了B÷A，结果得 $x$ ，那么B-A的正确结果为（）

A、 $2 x^{2} + 4 x - 6$ B、 $3 x + 6$ C、 $2 x^{2} + 6 x$ D、 $2 x^{2} + 4 x + 6$

查看试题解析
10. 我们称网格线的交点为格点．如图，在4×4的长方形网格中有两个格点A、B，连接AB，在网格中再找一个格点C，使得△ABC是等腰直角三角形，则满足条件的格点C的个数是（）

A、3 B、4 C、5 D、6

查看试题解析

二、填空题

11. 计算： $3^{- 2}$ =.

查看试题解析
12. 如图，AB＝CD，若要判定△ABD≌△CDB，则需要添加的一个条件是．

查看试题解析
13. 分解因式：3x²-6x+3= ．

查看试题解析
14. 如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，DF⊥AC于点F，S_△ABC＝21，DE＝3，AB＝9，则AC长是．

查看试题解析
15. 等腰三角形一腰上的高与另一腰的夹角为50°，则这个等腰三角形的一个底角的度数为．

查看试题解析
16. 按图所示的流程，若输出的A= -2，则输入的 $a$ 的值为．

查看试题解析
17. 已知 $\frac{a}{a - 4} = 2 - \frac{b}{b - 4}$ ，则 $a + b$ 的值为．

查看试题解析

三、解答题

18. 计算： $x (x + 2) + (1 + x) (1 - x)$

查看试题解析
19. 如图，在△ABC中，CE平分∠ACB交AB于点E，AD是△ABC边BC上的高，AD与CE相交于点F，且∠ACB＝80°，求∠AFE的度数．

查看试题解析
20. 先化简，再求值： $(\frac{x}{x - 1} - 1) \div \frac{x^{2} + 2 x + 1}{x^{2} - 1}$ ，其中x=-2

查看试题解析
21. 在如图所示的正方形网格中，每个小正方形的边长都是1，△ABC的顶点都在正方形网格的格点（网格线的交点）上．
⑴请在如图所示的网格平面内作出平面直角坐标系，使点A坐标为（1 ，3），点B坐标为（2 ，1）；
⑵请画出△ABC关于y轴对称的图形△A₁B₁C₁ ，并写出点B₁的坐标为 ▲ ；
⑶P为y轴上一点，当PB+PC的值最小时，P点的坐标为 ▲ ．

查看试题解析
22. 某学校在疫情期间用3000元购进A、B两种洗手液共550瓶，购买A种洗手液与购买B种洗手液的费用相同，且A种洗手液的单价是B种洗手液单价的1.2倍．

(1)、求B种洗手液的单价是多少元？

(2)、学校计划用不超过9800元的资金再次购进A、B两种洗手液共1800瓶，求A种洗手液最多能购进多少瓶？

查看试题解析
23. 如图，△ABC是等腰直角三角形，∠BAC=90°，△ACD是等边三角形，E为△ABC内一点，AC=CE，∠BAE=15°，AD与CE相交于点F．

(1)、求∠DFE的度数；

(2)、求证：AE=BE．

查看试题解析
24. 根据材料完成问题：
在含有两个字母的式子中，任意交换两个字母的位置，式子的值始终保持不变，像这样的式子我们称之为对称式，如： $\frac{1}{a} + \frac{1}{b}$ ， $a^{2} + b^{2}$ ，请解决下列问题：

(1)、① $a^{2} - b^{2}$ ；② $a^{2} b^{2}$ ③ $\frac{a^{2}}{b^{2}}$ 这3个式子中只有1个属于对称式：（请填序号）；

(2)、已知 $(x - a) (x - b) = x^{2} + m x + n$
①若 $m = 1$ ， $n = - 2$ ，求对称式 $a^{2} + b^{2}$ 的值；
②若 $m = - 3$ ， $n = 1$ ，当 $\frac{a^{2} - k}{a} + \frac{b^{2} - k}{b}$ ＞0时，求 $k$ 的取值范围．

查看试题解析
25. 如图，已知O为坐标原点，B（0 ，3），OB=CD，且OD=2OC，将△BOC沿BC翻折至△BEC，使得点E、O重合，点M是y轴正半轴上的一点且位于点B上方，以点B为端点作一条射线BA，使∠MBA=∠BCO，点F是射线BA上的一点．

(1)、请直接写出C、D两点的坐标：点C ，点D ；

(2)、当BF=BC时，连接FE．
①求点F的坐标；
②求此时△BEF的面积．

查看试题解析