广东省清远市阳山县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 下列各数中,是无理数的是( )A、 B、 C、 D、3.14152. 在﹣3,0,2,这组数中,最小的数是( )A、 B、﹣3 C、0 D、23. 如图,不能推出a∥b的条件是( )
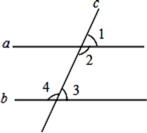 A、∠4=∠2 B、∠3+∠4=180° C、∠1=∠3 D、∠2+∠3=180°4. 甲、乙、丙、丁四名学生近4次数学测验成绩的平均数都是90分,方差分别是S甲2=5,S乙2=20,S丙2=23,S丁2=32,则这四名学生的数学成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁5. 下列各组数据中,能构成直角三角形的三边的长的一组是( )A、1,2,3 B、4,5,6 C、5,12,13 D、13,14,156. 下列运算正确的是( )A、 B、 C、 D、7. 已知是方程的解,则k的值为( )A、﹣2 B、2 C、4 D、﹣48. 如图,在△ABC中,∠C=90°,AC=3 ,BC=2.以AB为一条边向三角形外部作正方形,则正方形的面积是( )
A、∠4=∠2 B、∠3+∠4=180° C、∠1=∠3 D、∠2+∠3=180°4. 甲、乙、丙、丁四名学生近4次数学测验成绩的平均数都是90分,方差分别是S甲2=5,S乙2=20,S丙2=23,S丁2=32,则这四名学生的数学成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁5. 下列各组数据中,能构成直角三角形的三边的长的一组是( )A、1,2,3 B、4,5,6 C、5,12,13 D、13,14,156. 下列运算正确的是( )A、 B、 C、 D、7. 已知是方程的解,则k的值为( )A、﹣2 B、2 C、4 D、﹣48. 如图,在△ABC中,∠C=90°,AC=3 ,BC=2.以AB为一条边向三角形外部作正方形,则正方形的面积是( ) A、5 B、6 C、12 D、139. 在平面直角坐标系中,点A的坐标是(3a﹣5,a+1).若点A到x轴的距离与到y轴的距离相等,且点A在y轴的右侧,则a的值为( )A、1 B、2 C、3 D、1 或 310. 若直线y=kx+b经过第一、二、三象限,则函数y=bx﹣k的大致图象是( )A、
A、5 B、6 C、12 D、139. 在平面直角坐标系中,点A的坐标是(3a﹣5,a+1).若点A到x轴的距离与到y轴的距离相等,且点A在y轴的右侧,则a的值为( )A、1 B、2 C、3 D、1 或 310. 若直线y=kx+b经过第一、二、三象限,则函数y=bx﹣k的大致图象是( )A、 B、
B、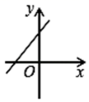 C、
C、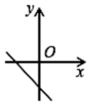 D、
D、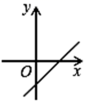
二、填空题
-
11. 9的算术平方根是 .12. 方程组的解是: .13. 一组数据:2,5,7,3,5的众数是 .14. 写出命题“两直线平行,同位角相等”的结论部分: .15. 如图,把一张三角形纸片(△ABC)进行折叠,使点A落在BC上的点F处,折痕为DE,点D,点E分别在AB和AC上,DE∥BC,若∠B=70°,则∠BDF的度数为 .
 16. 如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为 .
16. 如图,已知直线y=x+3与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为 . 17. 如图,直角坐标平面xOy内,动点P按图中箭头所示方向依次运动,第1次从点(-1,0)运动到点(0,1),第2次运动到点(1,0),第3次运动到点(2,-2),…按这样的运动规律,动点P第2022次运动到点的坐标是 .
17. 如图,直角坐标平面xOy内,动点P按图中箭头所示方向依次运动,第1次从点(-1,0)运动到点(0,1),第2次运动到点(1,0),第3次运动到点(2,-2),…按这样的运动规律,动点P第2022次运动到点的坐标是 .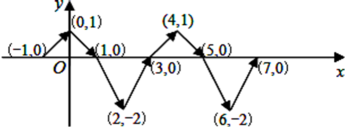
三、解答题
-
18. 计算:19. 如图,AB∥DG,∠1+∠2=180°.
 (1)、试说明:AD∥EF;(2)、若DG是∠ADC的平分线,∠2=142°,求∠B的度数.20. 如图所示,在平面直角坐标系中,已知A(0,1),B(3,0),C(3,4).
(1)、试说明:AD∥EF;(2)、若DG是∠ADC的平分线,∠2=142°,求∠B的度数.20. 如图所示,在平面直角坐标系中,已知A(0,1),B(3,0),C(3,4). (1)、在图中画出△ABC,△ABC的面积是 ▲ ;(2)、在(1)的条件下,延长线段CA,与x轴交于点M,则M点的坐标是 ▲ .(作图后直接写答案)21. 若实数的立方根为2,且实数 , , 满足 .(1)、求的值;(2)、若 , , 是△ABC的三边,试判断三角形的形状.22. 为了解某校八年级体育科目训练情况,从八年级学生中随机抽取了部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图请根据统计图中的信息解答下列问题:
(1)、在图中画出△ABC,△ABC的面积是 ▲ ;(2)、在(1)的条件下,延长线段CA,与x轴交于点M,则M点的坐标是 ▲ .(作图后直接写答案)21. 若实数的立方根为2,且实数 , , 满足 .(1)、求的值;(2)、若 , , 是△ABC的三边,试判断三角形的形状.22. 为了解某校八年级体育科目训练情况,从八年级学生中随机抽取了部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图请根据统计图中的信息解答下列问题: (1)、图1中的度数是 ▲ , 并把图2条形统计图补充完整.(2)、抽取的这部分的学生的体育科目测试结果的中位数是在级;(3)、依次将优秀、良好、及格、不及格记为90分、80分、70分、50分,请计算抽取的这部分学生体育的平均成绩.23. 某小区为了绿化环境,计划分两次购进A,B两种树苗,第一次购进A种树苗40棵,B种树苗15棵,共花费1750元;第二次购进A种树苗20棵,B种树苗6棵,共花费860元.(两次购进的A,B两种树苗各自的单价均不变)(1)、A,B两种树苗每棵的价格分别是多少元?(2)、因受季节影响,A种树苗价格下降10%,B种树苗价格上升20%,计划购进A种树苗25棵,B种树苗20棵,问总费用是多少元?24. 甲、乙两人从同一点出发,沿着跑道训练400米速度跑,乙比甲先出发,并且匀速跑完全程,甲出发一段时间后速度提高为原来的3倍.设乙跑步的时间为x(s),甲、乙跑步的路程分别为y1(米)、y2(米),y1、y2与x之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)、图1中的度数是 ▲ , 并把图2条形统计图补充完整.(2)、抽取的这部分的学生的体育科目测试结果的中位数是在级;(3)、依次将优秀、良好、及格、不及格记为90分、80分、70分、50分,请计算抽取的这部分学生体育的平均成绩.23. 某小区为了绿化环境,计划分两次购进A,B两种树苗,第一次购进A种树苗40棵,B种树苗15棵,共花费1750元;第二次购进A种树苗20棵,B种树苗6棵,共花费860元.(两次购进的A,B两种树苗各自的单价均不变)(1)、A,B两种树苗每棵的价格分别是多少元?(2)、因受季节影响,A种树苗价格下降10%,B种树苗价格上升20%,计划购进A种树苗25棵,B种树苗20棵,问总费用是多少元?24. 甲、乙两人从同一点出发,沿着跑道训练400米速度跑,乙比甲先出发,并且匀速跑完全程,甲出发一段时间后速度提高为原来的3倍.设乙跑步的时间为x(s),甲、乙跑步的路程分别为y1(米)、y2(米),y1、y2与x之间的函数图象如图所示,根据图象所提供的信息解答下列问题: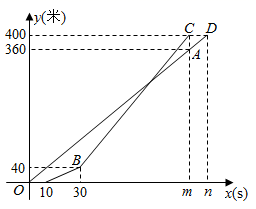 (1)、甲比乙晚出发s,甲提速前的速度是每秒米,m= , n=;(2)、当x为何值时,甲追上了乙?(3)、在甲提速后到甲、乙都停止的这段时间内,当甲、乙之间的距离不超过30米时,请你直接写出x的取值范围.25. 如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2).
(1)、甲比乙晚出发s,甲提速前的速度是每秒米,m= , n=;(2)、当x为何值时,甲追上了乙?(3)、在甲提速后到甲、乙都停止的这段时间内,当甲、乙之间的距离不超过30米时,请你直接写出x的取值范围.25. 如图,在平面直角坐标系中,过点C(0,6)的直线AC与直线OA相交于点A(4,2). (1)、求直线AC的表达式;(2)、求△OAC的面积;(3)、动点M在线段OA和射线AC上运动,是否存在点M,使△OMC的面积是△OAC的面积的 ?若存在,求出此时点M的坐标;若不存在,请说明理由。
(1)、求直线AC的表达式;(2)、求△OAC的面积;(3)、动点M在线段OA和射线AC上运动,是否存在点M,使△OMC的面积是△OAC的面积的 ?若存在,求出此时点M的坐标;若不存在,请说明理由。