广东省佛山市禅城区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 下列实数中,是无理数的是( )A、 B、 C、 D、2π2. 下列各组线段中,能构成直角三角形的一组是( )A、5,9,12 B、7,12,13 C、30,40,50 D、3,4,63. 在下列说法中,能确定位置的是( )A、禅城区季华五路 B、中山公园与火车站之间 C、距离祖庙300米 D、金马影剧院大厅5排21号4. 如图,AB∥CD,AE∥CF,∠A=41°,则∠C的度数为( )
 A、139° B、141° C、131° D、129°5. 已知x=2,y=﹣1是方程ax+y=3的一组解,则a的值为( )A、2 B、1 C、﹣1 D、﹣26. 已知点(﹣1,y1)、(2,y2)在函数y=﹣2x+1图象上,则y1与y2的大小关系是( )A、y1>y2 B、y1<y2 C、y1=y2 D、无法确定7. 下列运算正确的是( )A、 + = B、=4 C、=2× D、=﹣28. 如果你和其余6人进入了八年级速算比赛的总决赛,你想知道自己是否能进入前3名,只需要了解自己的成绩以及全部成绩的( )A、平均数 B、众数 C、中位数 D、方差9. 如图有一个水池,水面BE的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是( )
A、139° B、141° C、131° D、129°5. 已知x=2,y=﹣1是方程ax+y=3的一组解,则a的值为( )A、2 B、1 C、﹣1 D、﹣26. 已知点(﹣1,y1)、(2,y2)在函数y=﹣2x+1图象上,则y1与y2的大小关系是( )A、y1>y2 B、y1<y2 C、y1=y2 D、无法确定7. 下列运算正确的是( )A、 + = B、=4 C、=2× D、=﹣28. 如果你和其余6人进入了八年级速算比赛的总决赛,你想知道自己是否能进入前3名,只需要了解自己的成绩以及全部成绩的( )A、平均数 B、众数 C、中位数 D、方差9. 如图有一个水池,水面BE的宽为16尺,在水池的中央有一根芦苇,它高出水面2尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,则这个芦苇的高度是( ) A、26尺 B、24尺 C、17尺 D、15尺10. 已知一次函数y=kx+b的图象如图所示,则一次函数y=﹣bx+k的图象大致是( )
A、26尺 B、24尺 C、17尺 D、15尺10. 已知一次函数y=kx+b的图象如图所示,则一次函数y=﹣bx+k的图象大致是( )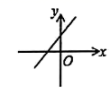 A、
A、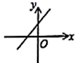 B、
B、 C、
C、 D、
D、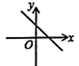 11. 下列命题中,是真命题的是( )A、如果a2=b2 , 则a=b B、三角形的外角大于任何一个与它不相邻的内角 C、无限小数都是无理数 D、=±412. 如图所示,∠B=∠C=90°,E是BC的中点,AE平分∠DAB,则下列说法正确的个数是( )
11. 下列命题中,是真命题的是( )A、如果a2=b2 , 则a=b B、三角形的外角大于任何一个与它不相邻的内角 C、无限小数都是无理数 D、=±412. 如图所示,∠B=∠C=90°,E是BC的中点,AE平分∠DAB,则下列说法正确的个数是( )⑴DE平分∠CDA;⑵△EBA≌△EDA;⑶△EBA≌△DCE;⑷AB+CD=AD;⑸AE2+DE2=AD2
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 的平方根是14. 如图,校园内有一块长方形草地,为了满足人们的多样化品求,在草地内拐角位置开出了一条路,走此路可以省m的路.
 15. 把一块直尺与一块直角三角板如图放置,若 ,则 的度数为 .
15. 把一块直尺与一块直角三角板如图放置,若 ,则 的度数为 . 16. 若关于x、y 的二元一次方程组的解满足x+y=1,则m的值为 .17. 我们知道是一个无理数,设它的整数部分为a,小数部分为b,则(+a)·b的值是 .18. 平面直角坐标系中,点O为坐标原点,点A(4,2)、点B(0,5),直线y=kx﹣2k+1恰好将△ABO平均分成面积相等的两部分,则k的值是 .
16. 若关于x、y 的二元一次方程组的解满足x+y=1,则m的值为 .17. 我们知道是一个无理数,设它的整数部分为a,小数部分为b,则(+a)·b的值是 .18. 平面直角坐标系中,点O为坐标原点,点A(4,2)、点B(0,5),直线y=kx﹣2k+1恰好将△ABO平均分成面积相等的两部分,则k的值是 .三、解答题
-
19.(1)、计算: ﹣ +(2)、解方程组:20. 如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(﹣2,1),B(﹣4,1),C(﹣3,2),D(﹣1,2).

⑴在图中画出四边形ABCD;
⑵在图中画出四边形ABCD关于x轴的对称图形A1B1C1D1 , 并分别写出点A、C的对应点A1、C1的坐标.
21. 某校举办弘扬中华传统知识演讲比赛,八(1)班计划从甲、乙两位同学中选出一位参加学校的决赛,已知这两位同学在预赛中各项成绩如表图: (1)、表中a的值为;b的值为 .(2)、把图中的统计图补充完整;(3)、若演讲内容、语言表达、形象风度、现场效果四项得分按30%、50%、10%、10%的权重比例计算两人的最终得分,并选择最终得分较高的同学作为代表参赛,那么谁将代表八(1)班参赛?请说明理由.
(1)、表中a的值为;b的值为 .(2)、把图中的统计图补充完整;(3)、若演讲内容、语言表达、形象风度、现场效果四项得分按30%、50%、10%、10%的权重比例计算两人的最终得分,并选择最终得分较高的同学作为代表参赛,那么谁将代表八(1)班参赛?请说明理由.项目
甲的成绩(分)
乙的成绩(分)
演讲内容
95
90
语言表达
90
85
形象风度
85
b
现场效果
90
95
平均分
a
90
22. 已知:如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点,∠AEG=∠AGE,∠C=∠DGC. (1)、求证:AB//CD;(2)、若∠AGE+∠AHF=180°,求证:∠B=∠C;(3)、在(2)的条件下,若∠BFC=4∠C,求∠D的度数.23. 学生准备组织八年级学生进行数学应用创作大赛,需购买甲、乙两种奖品.如果购买甲奖品2个和乙奖品5个,需花费66元:购买甲奖品3个和乙奖品2个,需花费44元;(1)、求甲、乙两种奖品的单价各是多少元?(2)、由于临时有变,只买甲、乙一种奖品即可,且甲奖品按原价8折销售,乙奖品购买8个以内按原价出售,购买8个以上超出的部分按原价的5折销售,设购买x个甲奖品需要y1元,购买x个乙奖品需要y2元,请用x分别表示出y1和y2;(3)、在(2)的条件下,问买哪一种产品更省钱?24. 如图所示,平面直角坐标系中,直线AB交x轴于点B(﹣3,0),交y轴于点A(0,1),直线x=﹣1交AB于点D,P是直线x=﹣1上一动点,且在点D上方,设P(﹣1,n).
(1)、求证:AB//CD;(2)、若∠AGE+∠AHF=180°,求证:∠B=∠C;(3)、在(2)的条件下,若∠BFC=4∠C,求∠D的度数.23. 学生准备组织八年级学生进行数学应用创作大赛,需购买甲、乙两种奖品.如果购买甲奖品2个和乙奖品5个,需花费66元:购买甲奖品3个和乙奖品2个,需花费44元;(1)、求甲、乙两种奖品的单价各是多少元?(2)、由于临时有变,只买甲、乙一种奖品即可,且甲奖品按原价8折销售,乙奖品购买8个以内按原价出售,购买8个以上超出的部分按原价的5折销售,设购买x个甲奖品需要y1元,购买x个乙奖品需要y2元,请用x分别表示出y1和y2;(3)、在(2)的条件下,问买哪一种产品更省钱?24. 如图所示,平面直角坐标系中,直线AB交x轴于点B(﹣3,0),交y轴于点A(0,1),直线x=﹣1交AB于点D,P是直线x=﹣1上一动点,且在点D上方,设P(﹣1,n). (1)、求直线AB的解析式;(2)、求△ABP的面积(用含n的代数式表示);(3)、点C是y轴上一点,当S△ABP=2时,△BPC是等腰三角形,
(1)、求直线AB的解析式;(2)、求△ABP的面积(用含n的代数式表示);(3)、点C是y轴上一点,当S△ABP=2时,△BPC是等腰三角形,①满足条件的点C的个数是 ▲ 个(直接写出结果);
②当BP为等腰三角形的底边时,求点C的坐标.