广东省东莞市四校联考2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 办公中常用的纸张一般A4纸其厚度为0.0075m，将0.0075用科学记数法表示为（）

A、75×10^﹣4 B、75×10^﹣3 C、7.5×10^﹣3 D、0.75×10^﹣2

查看试题解析
3. 下列各组中的三条线段恰好是一个三角形三条边的是（）

A、3，4，7 B、3，4，10 C、3，7，10 D、4，7，10

查看试题解析
4. 若分式 $\frac{x}{2 - x}$ 有意义，则x的取值范围是（）

A、x＞2 B、x≠0 C、x≠0且x≠2 D、x≠2

查看试题解析
5. 下列计算正确的是（）

A、b³•b³＝2b³ B、（a⁵）²＝a⁷ C、（﹣2a）²＝4a² D、（ab）⁵÷（ab）²＝ab³

查看试题解析
6. 若一个多边形的内角和等于 $1800 °$ ，这个多边形的边数是（）

A、6 B、8 C、10 D、12

查看试题解析
7. 如图，在△ABC和△DEF中，∠A＝∠D，AF＝DC，添加下列条件中的一个仍无法证明△ABC≌△DEF的是（）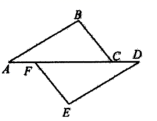

A、BC＝EF B、AB＝DE C、∠B＝∠E D、∠ACB＝∠DFE

查看试题解析
8. 如图，在△ABC中，∠C＝90°，DE垂直平分AB，分别交AB、BC于点D、E，若∠CAE＝∠B+15°，则∠B的度数为（　　）

A、15° B、35° C、25° D、20°

查看试题解析
9. 如果x²﹣3x+k（k是常数）是完全平方式，那么k的值为（）

A、6 B、9 C、 $\frac{3}{2}$ D、 $\frac{9}{4}$

查看试题解析
10. 如图，已知∠MON＝30°，点A₁ ， A₂ ， A₃ ， …在射线ON上，点B₁ ， B₂ ， B₃ ， …在射线OM上，△A₁B₁A₂ ， △A₂B₂A₃ ， △A₃B₃A₄ ， …均为等边三角形，若OA₁＝2，则△A₆B₆A₇的边长为（）

A、16 B、32 C、64 D、128

查看试题解析

二、填空题

11. 计算： ${(π - 3)}^{0} + {(\frac{1}{2})}^{- 1}$ ＝．

查看试题解析
12. 如图，∠ABD＝80°，∠C＝38°，则∠D＝度．

查看试题解析
13. 若 $△ A B C ≌ △ A B D$ ， $B C = 4$ ， $A C = 5$ ， $A B = 2$ ，则AD的长为．

查看试题解析
14. 已知x+y＝﹣2，xy＝4，则x²y+xy²＝

查看试题解析
15. （x+2）（3x﹣5）=3x²﹣bx﹣10，则b= ．

查看试题解析
16. 在△ABC中，∠B=60°，∠C=40°，AD、AE分别是△ABC的高线和角平分线，则∠DAE的度数为．

查看试题解析
17. 在等腰三角形ABC中，∠A＝3∠B，则∠C的度数为.

查看试题解析

三、解答题

18. 化简：（x﹣2）²﹣x（x+4）．

查看试题解析
19. 如图，在平面直角坐标系中，△ABC三个顶点的坐标为A（1，2），B（4，1），C（2，4）．
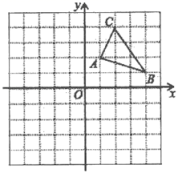
⑴在图中画出△ABC关于y轴对称的图形△A′B′C′；并写出点B′的坐标．
⑵在图中x轴上作出一点P，使PA+PB的值最小．

查看试题解析
20. 已知：如图，AD是等腰三角形ABC的底边BC上的中线，DE∥AB，交AC于点E．求证：△AED是等腰三角形．

查看试题解析
21. 如图所示，BE＝CF，DE⊥AB于E，DF⊥AC于F，且BD＝CD．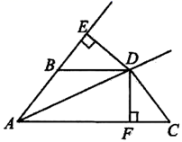

求证：

(1)、△BDE≌△CDF；

(2)、AD是∠BAC的平分线．

查看试题解析
22. 先化简，再求值： $\frac{a^{2} - 2 a b + b^{2}}{a^{2} - b^{2}} \div \frac{a^{2} - a b}{a} - \frac{2}{a + b}$ ，其中a＝2，b＝﹣1．

查看试题解析
23. 六一儿童节来临之际，某商店用3000元购进一批玩具，很快售完；第二次购进时，每件的进价提高了20%，同样用3000元购进的数量比第一次少了10件．

(1)、求第一次每件的进价为多少元？

(2)、若两次购进的玩具售价均为70元，且全部售完，求两次的总利润为多少元？

查看试题解析
24. 从边长为a的正方形中减掉一个边长为b的正方形（如图1），然后将剩余部分拼成一个长方形（如图2）．

(1)、上述操作能验证的等式是；

(2)、运用你从（1）写出的等式，完成下列各题：
①已知：a﹣b＝3，a²﹣b²＝21，求a+b的值；
②计算： $(1 - \frac{1}{2^{2}}) \times (1 - \frac{1}{3^{2}}) \times (1 - \frac{1}{4^{2}}) \times ⋯ \times (1 - \frac{1}{202 0^{2}}) \times (1 - \frac{1}{202 1^{2}})$ ．

查看试题解析
25. 如图，在平面直角坐标系中，点A的坐标为（1，0），以线段OA为边在第四象限内作等边△AOB，点C为x轴正半轴上一动点（OC＞1），连接BC，以线段BC为边在第四象限内作等边△CBD，连接DA并延长交y轴于点E．

(1)、求证：△OBC≌△ABD．

(2)、在点C的运动过程中，∠CAD的度数是否会变化？如果不变，请求出∠CAD的度数；如果变化，请说明理由．

(3)、当点C运动到什么位置时，以A，E，C为顶点的三角形是等腰三角形？

查看试题解析