北京市燕山区2021-2022学年八年级上学期期末质量监测数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 第24届冬奥会将于2022年2月4日至20日在北京市和张家口市联合举行．下面是从历届冬奥会的会徽中选取的部分图形，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 5G是第五代移动通信技术，应用5G网络下载一个1000KB的文件只需要0.00076秒，下载一部高清电影只需要1秒．将0.00076用科学记数法表示应为（）

A、 $76 \times 1 0^{- 5}$ B、 $7.6 \times 1 0^{- 4}$ C、 $7.6 \times 1 0^{- 5}$ D、 $0.76 \times 1 0^{- 3}$

查看试题解析
3. 下列运算正确的是（）

A、x²＋x²＝2x⁴ B、x²∙x³＝x⁶ C、(x²)³＝x⁶ D、(－2x)²＝－4x²

查看试题解析
4. 如图，工人师傅在安装木制门框时，为防止变形，常常钉上两条斜拉的木条，这样做的数学依据是（）

A、两点确定一条直线 B、两点之间，线段最短 C、三角形具有稳定性 D、三角形的任意两边之和大于第三边

查看试题解析
5. 已知一个正方形的边长为a＋1，则该正方形的面积为（）

A、a²＋2a＋1 B、a²－2a＋1 C、a²＋1 D、4a＋4

查看试题解析
6. 若一个多边形的内角和为1080°，则这个多边形的边数为（）

A、5 B、6 C、7 D、8

查看试题解析
7. 如图，等腰△ABC中，AB＝AC，点D是BC边中点，则下列结论错误的是（）

A、B＝C B、AD⊥BC C、∠BAD＝∠CAD D、AB＝2BC

查看试题解析
8. 如图，Rt△ABC中，B＝90，点P在边AB上，CP平分∠ACB，PB＝3cm，AC＝10cm，则△APC的面积是（）

A、15cm² B、22.5cm² C、30cm² D、45cm²

查看试题解析
9. 如图，正方形网格中， A，B两点均在直线a上方，要在直线a上求一点P，使PA＋PB的值最小，则点P应选在（）

A、C点 B、D点 C、E点 D、F点

查看试题解析
10. 如图，△ABC中，AB＜AC＜BC，如果要用尺规作图的方法在BC上确定一点P，使PA＋PB＝BC，那么符合要求的作图痕迹是（）

A、 B、 C、 D、

查看试题解析

二、填空题

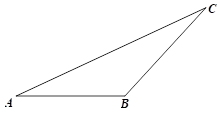
11. 若分式 $\frac{x - 4}{2 x + 1}$ 的值为0，则x的值为．

查看试题解析
12. 如图，已知△ABC，通过测量、计算得△ABC的面积约为cm².（结果保留一位小数）

查看试题解析
13. 如图，线段AC与BD相交于点O，∠A＝∠D＝90°，要证明△ABC≌△DCB，还需添加的一个条件是． (只需填一个条件即可)

查看试题解析
14. 计算： $3 a^{3} \cdot 2 a$ ＋ $a^{6}$ ÷ $a^{2}$ ＝．

查看试题解析
15. 图中的四边形均为长方形，根据图形，写出一个正确的等式：．

查看试题解析
16. 如图，等腰△ABC中，AB＝AC，A＝40，点D在边AC上，ADB＝100，则DBC的度数为 °．

查看试题解析
17. “有一种速度叫中国速度，有一种骄傲叫中国高铁．”快速发展的中国高速铁路，正改变着中国人的出行方式．下表是从北京到上海的两次列车的相关信息：
出行方式
出发站－到达站
路程
平均速度
特快列车T109
北京－上海
全程1463km
98 km/h
高铁列车G27
北京南－上海虹桥
全程1325km
x km/h
已知从北京到上海乘坐G27次高铁列车比T109次特快列车用时少10小时26分钟．设G27次高铁列车的平均速度为x km/h，根据题意可列方程为．

查看试题解析
18. 如图，∠ACB＝90°，AC＝BC，AD⊥CD于点D，BE⊥CD于点E，有下面四个结论：① △CAD≌△BCE； ② ∠ABE＝∠BAD； ③ AB＝CD； ④ CD＝AD＋DE．其中所有正确结论的序号是．

查看试题解析

三、解答题

19. 计算：

(1)、 ${(2 - π)}^{0} + (\frac{1}{2})^{- 1} - ｜ - 2 ｜$ ；

(2)、 $\frac{2}{a + 1} + \frac{2 a}{a + 1}$ ．

查看试题解析
20. 分解因式： $x^{3} - 9 x$ ．

查看试题解析
21. 解方程： $\frac{x}{x - 5} - \frac{3}{x + 5} = 1$ ．

查看试题解析
22. 如图，E为AB上一点，BD∥AC，AB＝BD，AC＝BE．求证：BC＝DE．

查看试题解析
23. 数学课上，王老师布置如下任务：
如图，已知∠MAN＜45°，点B是射线AM上的一个定点，在射线AN上求作点C，使∠ACB＝2∠A．
下面是小路设计的尺规作图过程．
作法：①作线段AB的垂直平分线l，直线l交射线AN于点D；
②以点B为圆心，BD长为半径作弧，交射线AN于另一点C，则点C即为所求．
根据小路设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形；(保留作图痕迹)

(2)、完成下面的证明：
证明：连接BD，BC，
∵直线l为线段AB的垂直平分线，
∴DA＝ ▲ ， ( ▲ )（填推理的依据）
∴∠A＝∠ABD，
∴∠BDC＝∠A＋∠ABD＝2∠A．
∵BC＝BD，
∴∠ACB＝∠ ▲ ， ( ▲ )（填推理的依据）
∴∠ACB＝2∠A．

查看试题解析
24. 求代数式 $(\frac{a}{a - 1} - 1)$ ÷ $\frac{a^{2} + a}{a^{2} - 1}$ 的值，其中 $a$ ＝ $\frac{2}{3}$ ．

查看试题解析
25. 列方程解应用题：
“共和国勋章”获得者，“杂交水稻之父”袁隆平院士一生致力于提高水稻的产量，为解决人类温饱问题做出了巨大贡献．某农业基地现有A，B两块试验田，A块种植普通水稻，B块种植杂交水稻．已知杂交水稻的亩产量是普通水稻亩产量的1.8倍，A块试验田种植面积比B块试验田多5亩，两块试验田的总产量都是6750千克．求杂交水稻的亩产量是多少千克？

查看试题解析
26. 阅读下列材料：
利用完全平方公式，可以把多项式 $x^{2} + b x + c$ 变形为 $(x + m)^{2} + n$ 的形式．例如， $x^{2} - 4 x + 3$ ＝ $x^{2} - 4 x + 4 - 4 + 3$ ＝ $(x - 2)^{2} - 1$ ．
观察上式可以发现，当 $x - 2$ 取任意一对互为相反数的值时，多项式 $x^{2} - 4 x + 3$ 的值是相等的．例如，当 $x - 2$ ＝±1，即 $x$ ＝3或1时， $x^{2} - 4 x + 3$ 的值均为0；当 $x - 2$ ＝±2，即 $x$ ＝4或0时， $x^{2} - 4 x + 3$ 的值均为3．
我们给出如下定义：
对于关于 $x$ 的多项式，若当 $x + m$ 取任意一对互为相反数的值时，该多项式的值相等，则称该多项式关于 $x$ ＝ $- m$ 对称，称 $x$ ＝ $- m$ 是它的对称轴．例如， $x^{2} - 4 x + 3$ 关于 $x$ ＝2对称， $x$ ＝2是它的对称轴．
请根据上述材料解决下列问题：

(1)、将多项式 $x^{2} - 6 x + 5$ 变形为 $(x + m)^{2} + n$ 的形式，并求出它的对称轴；

(2)、若关于 $x$ 的多项式 $x^{2} + 2 a x - 1$ 关于 $x$ ＝－5对称，则 $a$ ＝；

(3)、代数式 $(x^{2} + 2 x + 1) (x^{2} - 8 x + 16)$ 的对称轴是 $x$ ＝．

查看试题解析
27. 如图，在等边△ABC中，点P是BC边上一点，∠BAP＝ $α$ （30°＜ $α$ ＜60°），作点B关于直线AP的对称点D，连接DC并延长交直线AP于点E，连接BE．

(1)、依题意补全图形，并直接写出∠AEB的度数；

(2)、用等式表示线段AE，BE，CE之间的数量关系，并证明．
分析：①涉及的知识要素：图形轴对称的性质；等边三角形的性质；全等三角形的判定与性质……
②通过截长补短，利用60°角构造等边三角形，进而构造出全等三角形，从而达到转移边的目的．
请根据上述分析过程，完成解答过程．

查看试题解析
28. 在平面直角坐标系xOy中，直线l：x＝m表示经过点(m，0)，且平行于y轴的直线．给出如下定义：将点P关于x轴的对称点 $P_{1}$ ，称为点P的一次反射点；将点 $P_{1}$ 关于直线l的对称点 $P_{2}$ ，称为点P关于直线l的二次反射点．例如，如图，点M(3，2)的一次反射点为 $M_{1}$ (3，－2)，点M关于直线l：x＝1的二次反射点为 $M_{2}$ (－1，－2)．
已知点A(－1，－1)，B(－3，1)，C(3，3)，D(1，－1)．

(1)、点A的一次反射点为，点A关于直线 $l_{1}$ ：x＝2的二次反射点为；

(2)、点B是点A关于直线 $l_{2}$ ：x＝a的二次反射点，则a的值为；

(3)、设点A，B，C关于直线 $l_{3}$ ：x＝t的二次反射点分别为 $A_{2}$ ， $B_{2}$ ， $C_{2}$ ，若△ $A_{2}$ $B_{2}$ $C_{2}$ 与△BCD无公共点，求t的取值范围．

查看试题解析

出行方式	出发站－到达站	路程	平均速度
特快列车T109	北京－上海	全程1463km	98 km/h
高铁列车G27	北京南－上海虹桥	全程1325km	x km/h