北京市通州区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 在下列国际货币符号中,为轴对称图形的是( )A、
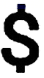 B、
B、 C、
C、 D、
D、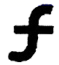 2. 已知代数式的值为0,则的值为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 在下列四个选项中,数值最接近的是( )A、2 B、3 C、4 D、55. 一个不透明的盒子中装有2个白球,5个红球,这些球除颜色外其他都相同.则在下列说法中正确的是( )A、无放回的从中连续摸出三个红球是随机事件 B、从中摸出一个棕色球是随机事件 C、无放回的从中连续摸出两个白球是不可能事件 D、从中摸出一个红色球是必然事件6. 如图,在中, , , 垂足为 . 如果 , , 则的长为( )
2. 已知代数式的值为0,则的值为( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 在下列四个选项中,数值最接近的是( )A、2 B、3 C、4 D、55. 一个不透明的盒子中装有2个白球,5个红球,这些球除颜色外其他都相同.则在下列说法中正确的是( )A、无放回的从中连续摸出三个红球是随机事件 B、从中摸出一个棕色球是随机事件 C、无放回的从中连续摸出两个白球是不可能事件 D、从中摸出一个红色球是必然事件6. 如图,在中, , , 垂足为 . 如果 , , 则的长为( ) A、2 B、 C、 D、7. 如图是一个可以自由转动的转盘,转盘分成4个大小相同的扇形,颜色分为灰、白二种颜色.指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向白色区域的概率是( )
A、2 B、 C、 D、7. 如图是一个可以自由转动的转盘,转盘分成4个大小相同的扇形,颜色分为灰、白二种颜色.指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向白色区域的概率是( )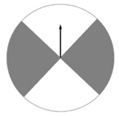 A、 B、 C、 D、18. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 - =20 B、 - =20 C、 - = D、 =
A、 B、 C、 D、18. 八年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了20分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为x千米/小时,则所列方程正确的是( )A、 - =20 B、 - =20 C、 - = D、 =二、填空题
-
9. 4的算术平方根是 .10. 化简分式的结果是 .11. 若代数式在实数范围内有意义,则实数的取值范围是 .12. 化简: =.13. 有两个正方体的积木块,如图所示.

下面是小怡投掷某块积木200次的情况统计表:
灰色的面朝上
白色的面朝上
32次
168次
根据表中的数据推测,小怡最有可能投掷的是号积木.
14. 如图,线段 , 垂足为点 , 线段分别交、于点 , , 连结 , . 则的度数为 .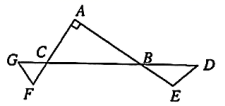 15. 小豪发现一个命题:“如果两个无理数 , , 满足 , 那么这两个无理数的和是无理数.”这个命题是(填写“真命题”,“假命题”);请你举例说明 .16. 在新年联欢会上,老师设计了“你说我画”的游戏.游戏规则如下:甲同学需要根据乙同学提供的三个条件画出形状和大小都确定的三角形.已知乙同学说出的前两个条件是“ , ”.现仅存下列三个条件:①;②;③ . 为了甲同学画出形状和大小都确定的 , 乙同学可以选择的条件有: . (填写序号,写出所有正确答案)
15. 小豪发现一个命题:“如果两个无理数 , , 满足 , 那么这两个无理数的和是无理数.”这个命题是(填写“真命题”,“假命题”);请你举例说明 .16. 在新年联欢会上,老师设计了“你说我画”的游戏.游戏规则如下:甲同学需要根据乙同学提供的三个条件画出形状和大小都确定的三角形.已知乙同学说出的前两个条件是“ , ”.现仅存下列三个条件:①;②;③ . 为了甲同学画出形状和大小都确定的 , 乙同学可以选择的条件有: . (填写序号,写出所有正确答案)三、解答题
-
17. 《几何原本》是一部集前人思想和欧几里得个人创造性一体的不朽之作,把人们公认的一些事实列成定义、公理和公设,用它们来研究各种几何图形的性质,从而建立了一套从定义、公理和公设出发,论证命题得到定理的几何学论证方法.小牧在学习过程中产生了一个猜想:“如果三角形一边上的中线的长度等于所在边长度的一半,那么这个三角形是直角三角形.”
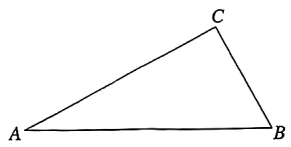 (1)、请你用尺规作图,在图中作出线段的中点 , 并连接 . (保留作图痕迹)(2)、请你结合图形,将小牧猜想的命题写成已知、求证.
(1)、请你用尺规作图,在图中作出线段的中点 , 并连接 . (保留作图痕迹)(2)、请你结合图形,将小牧猜想的命题写成已知、求证.已知: .
求证:为直角三角形.
(3)、补全上述猜想的证明过程.证明:∵点是线段的中点,
∴ ,
又∵ ,
∴ ,
在中,∵ ,
∴ , ( ▲ )(填推理的依据),
同理,在中, .
在中
∵ .
∴ ▲ ,
∴在中, ,
∴为直角三角形.
18. 计算: .19. 计算: .20. 已知 ,求代数式 的值.21. 解方程:22. 已知:如图,中, , , 分别是 , 的平分线.请你写出图中的一对全等三角形,并证明.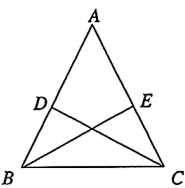 23. 如图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段的端点都在格点上.要求以为边画一个等腰 , 且使得点为格点.请在下面的网格图中画出3种不同的等腰 .
23. 如图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段的端点都在格点上.要求以为边画一个等腰 , 且使得点为格点.请在下面的网格图中画出3种不同的等腰 .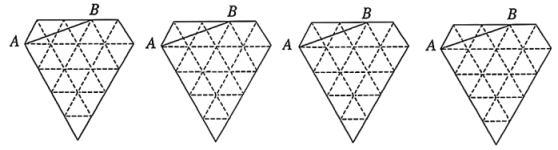 24. 列分式方程解应用题:某种型号的LED显示屏为长方形,其长与宽的比为;若将该显示屏的长、宽各减少2cm,则其长与宽的比值将会变为 . 求该型号LED显示屏的长度与宽度.25. 如图,在中, , , 在中, , 与交于点 , 且 . 求证:
24. 列分式方程解应用题:某种型号的LED显示屏为长方形,其长与宽的比为;若将该显示屏的长、宽各减少2cm,则其长与宽的比值将会变为 . 求该型号LED显示屏的长度与宽度.25. 如图,在中, , , 在中, , 与交于点 , 且 . 求证: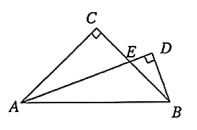 (1)、;(2)、 .26. 北宋科学家沈括在《梦溪笔谈》中曾记载了宋代行军时的后勤供应情况:人负米六斗,卒自携一斗,人食日二升.其大意为,在行军过程中,民夫可以背负六斗(60升)米,士兵可以自己背一斗(10升)米,民夫(士兵)每人一天行军会消耗2升米.(1)、若每个士兵雇佣4个民夫随其一同行军,则在没有其他粮食补充的情况下,背负的米支持行军的天数为天;(2)、若每个士兵雇佣个民夫随其一同行军,则在没有其他粮食补充的情况下,背负的米支持行军的天数为(用含有的代数式表示);如果每个士兵雇佣的民夫数量没有上限,在没有其他粮食补充的情况下,背负的米支持的行军天数有没有上限? (回答“有”或者“没有”)请你说明理由.27. 如图, , 点与点关于射线对称,连接 . 点为射线上任意一点,连接 . 将线段绕点顺时针旋转60°,得到线段 , 连接 .
(1)、;(2)、 .26. 北宋科学家沈括在《梦溪笔谈》中曾记载了宋代行军时的后勤供应情况:人负米六斗,卒自携一斗,人食日二升.其大意为,在行军过程中,民夫可以背负六斗(60升)米,士兵可以自己背一斗(10升)米,民夫(士兵)每人一天行军会消耗2升米.(1)、若每个士兵雇佣4个民夫随其一同行军,则在没有其他粮食补充的情况下,背负的米支持行军的天数为天;(2)、若每个士兵雇佣个民夫随其一同行军,则在没有其他粮食补充的情况下,背负的米支持行军的天数为(用含有的代数式表示);如果每个士兵雇佣的民夫数量没有上限,在没有其他粮食补充的情况下,背负的米支持的行军天数有没有上限? (回答“有”或者“没有”)请你说明理由.27. 如图, , 点与点关于射线对称,连接 . 点为射线上任意一点,连接 . 将线段绕点顺时针旋转60°,得到线段 , 连接 .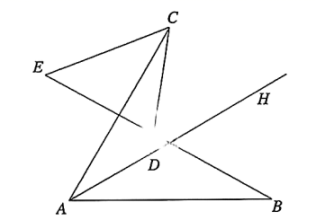 (1)、求证:直线是线段的垂直平分线;(2)、点是射线上一动点,请你直接写出与之间的数量关系.
(1)、求证:直线是线段的垂直平分线;(2)、点是射线上一动点,请你直接写出与之间的数量关系.