北京市门头沟区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{3}$ 的相反数是（）

A、 $\sqrt{3}$ B、 $- \sqrt{3}$ C、 $\pm \sqrt{3}$ D、 $\frac{\sqrt{3}}{3}$

查看试题解析
2. 以下四大通讯运营商的企业图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如果分式 $\frac{x - 3}{x + 1}$ 的值等于0，那么x的值是（）

A、 $x = - 1$ B、 $x = 3$ C、 $x \geq - 1$ D、 $x \neq 3$

查看试题解析
4. 下列事件中，属于必然事件的是（）

A、13人中至少有2个人生日在同月 B、任意掷一枚质地均匀的硬币，落地后正面朝上 C、从一副扑克牌中随机抽取一张，抽到的是红桃A D、以长度分别是3cm，4cm，6cm的线段为三角形三边，能构成一个直角三角形

查看试题解析
5. 下列等式成立的是（）

A、 $\frac{a + 1}{b + 1} = \frac{a}{b}$ B、 $\frac{- 2 a + 1}{- 2 b} = \frac{a + 1}{b}$ C、 $\frac{b - a}{a - b} = - 1$ D、 $\frac{a}{b} = \frac{a^{2}}{b^{2}}$

查看试题解析
6. 下列计算正确的是（）

A、 ${(- \sqrt{3})}^{2} = 3$ B、 $\sqrt{{(- 3)}^{2}} = - 3$ C、 $\sqrt{\frac{1}{2}} = 2 \sqrt{2}$ D、 $3 \sqrt{2} = \sqrt{3 \times 2}$

查看试题解析
7. 如图，在△ABC中，AB＝AC，∠A＝36°，分别以A，C为圆心，大于 $\frac{1}{2} A C$ 的同样长为半径作弧，两弧分别交于点M，N，作直线MN，分别交AB，AC于点D，E，连接CD．有以下四个结论：①∠BCD＝∠ACD＝36°；②AD＝CD＝CB；③_△BCD的周长等于AC＋BC；④点D是线段AB的中点．其中正确的结论是（）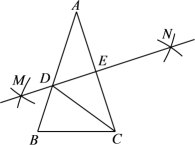

A、①② B、③④ C、①②③ D、①②③④

查看试题解析
8. 如图，在2×2正方形网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，图中的△ABC为格点三角形，在图中可以画出与△ABC成轴对称的格点三角形的个数为（）

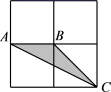A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

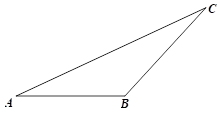
9. 4的算术平方根是．

查看试题解析
10. 如果二次根式 $\sqrt{x - 5}$ 有意义，那么x的取值范围是．

查看试题解析
11. 如图，已知△ABC，通过测量、计算得△ABC的面积约为cm².（结果保留一位小数）

查看试题解析
12. 一个转盘盘面被分成6块全等的扇形区域，其中2块是红色，4块是蓝色．用力转动转盘，当转盘停止后，指针对准红色区域的可能性大小是．

查看试题解析
13. 一个等腰三角形的两边长分别为 $3 cm$ 和 $7 cm$ ，则它的周长为 $cm$ .

查看试题解析
14. 如图，数轴上点A，B对应的实数分别是 $- 1$ ， 2，点C在线段AB上运动，如果点C表示无理数，那么点C可以是（写出一个即可）．

查看试题解析
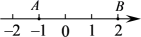15. 如图，D为△ABC内一点，AD⊥CD，AD平分∠CAB，且∠DCB＝∠B．如果AB＝10，AC＝6，那么CD＝．

查看试题解析
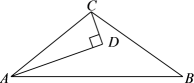16. 如图，在△AB₁C₁中，AC₁＝B₁C₁ ， ∠C₁＝20°，在B₁C₁上取一点C₂ ，延长AB₁到点B₂ ，使得B₁B₂＝B₁C₂ ，在B₂C₂上取一点C₃ ，延长AB₂到点B₃ ，使得B₂B₃＝B₂C₃ ，在B₃C₃上取一点C₄ ，延长AB₃到点B₄ ，使得B₃B₄＝B₃C₄ ， ……，按此操作进行下去，那么第2个三角形的内角∠AB₂C₂＝°；第n个三角形的内角∠AB_nC_n＝°．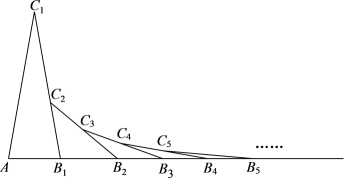

查看试题解析

三、解答题

17. 计算：

(1)、 $\frac{3 x}{x + 2} + \frac{6}{x + 2}$ ；

(2)、 $4 a b^{2} \div {(\frac{- b}{a})}^{2}$ ．

查看试题解析
18. 计算：

(1)、 $\sqrt{8} - \sqrt[3]{27} + | \sqrt{2} - 3 |$ ；

(2)、 $(2 + \sqrt{3}) (2 - \sqrt{3}) - \sqrt{18} \div \sqrt{2}$ ．

查看试题解析
19. 解方程： $\frac{x}{x - 3} - \frac{3}{{(x - 3)}^{2}} = 1$ ．

查看试题解析
20. 如图，AD，BC相交于点O，AO＝DO．

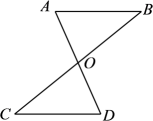(1)、如果只添加一个条件，使得△AOB≌△DOC，那么你添加的条件是（要求：不再添加辅助线，只需填一个答案即可）；

(2)、根据已知及（1）中添加的一个条件，证明AB＝DC．

查看试题解析
21. 已知 $x^{2} + 2 x - 5 = 0$ ，求代数式 $(x + 1 - \frac{3}{x - 1}) \div \frac{x - 2}{x^{2} - x}$ 的值．

查看试题解析
22. 学习分式运算过程中，老师布置了这样一个任务：依据下面的流程图，计算 $\frac{a}{a - b} - \frac{2 a b}{a^{2} - b^{2}}$ ．

(1)、依据上面流程图计算 $\frac{a}{a - b} - \frac{2 a b}{a^{2} - b^{2}}$ 时，需要经历的路径是（只填写序号）；

(2)、依据（1）中路径写出正确解答过程．

查看试题解析
23. 下面是小丽同学设计的“作30°角”的尺规作图过程．
已知：如图1，射线OA．
求作：∠AOB，使∠AOB ＝30°．
作法：如图2，
①在射线OA上任取一点C；
②分别以O，C为圆心，OC长为半径作弧，两弧在射线OA的上方交于点D，作射线OD，并连接CD；
③以O为圆心，任意长为半径作弧，分别交射线OA，OD于点E，F；
④分别以E，F为圆心，以大于 $\frac{1}{2} E F$ 的同样长为半径作弧，两弧在∠AOD内部交于点B；
⑤作射线OB；
∴ ∠AOB就是所求的角．
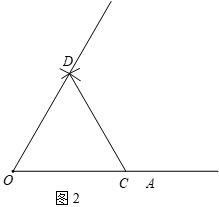
根据小丽设计的尺规作图过程，解答下列问题：

(1)、使用直尺和圆规，依作法补全图2（保留作图痕迹）；

(2)、补全下面证明过程：
证明：连接BE，BF．
∵ OC＝OD＝CD，
∴ △OCD是等边三角形．
∴∠COD＝                  ▲                        °．
又∵ OE ＝OF，BE ＝ BF，OB＝OB，
∴ △OEB≌△OFB（                  ▲                              ）（填推理依据）．
∴ ∠EOB＝∠FOB（                        ▲                        ）（填推理依据）．
∴ ∠AOB ＝ $\frac{1}{2} ∠ C O D$ ＝30°．
∴∠AOB就是所求的角．

查看试题解析
24. 列方程解应用题：
第24届冬奥会将于2022年2月在中国北京和张家口举行．为了迎接冬奥会，某公司接到制作12000件冬奥会纪念品的订单．为了尽快完成任务，该公司实际每天制作纪念品的件数是原计划每天制作纪念品件数的1.2倍，结果提前10天完成任务，求原计划每天制作多少件冬奥会纪念品？

查看试题解析
25. 已知，如图，在△ABC中，∠C＝ 90°，AD平分∠BAC交BC于D，过D作DE∥AC交AB于E．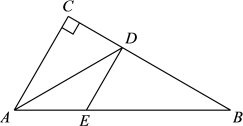

(1)、求证：AE＝DE；

(2)、如果AC＝3， $A D = 2 \sqrt{3}$ ，求AE的长．

查看试题解析
26. 阅读理解：
材料：小华在学习分式运算时，通过具体运算： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ， $\frac{1}{4 \times 5} = \frac{1}{4} - \frac{1}{5}$ ， …，
发现规律： $\frac{1}{n \times (n + 1)} = \frac{1}{n} - \frac{1}{n + 1}$ （ $n$ 为正整数），并证明了此规律成立．
应用规律，快速计算： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + ⋯ + \frac{1}{9 \times 10} = 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + ⋯ + \frac{1}{9} - \frac{1}{10} = 1 - \frac{1}{10} = \frac{9}{10}$ ．
根据材料，回答问题：
在学习二次根式运算时，小华根据分式学习积累的活动经验，类比探究二次根式的运算规律，并解决问题．请将下面的探究过程，补充完整．

(1)、具体运算：
特例1： $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1 \times 2} = 1 + 1 - \frac{1}{2}$ ，
特例2： $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2 \times 3} = 1 + \frac{1}{2} - \frac{1}{3}$ ，
特例3： $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3 \times 4} = 1 + \frac{1}{3} - \frac{1}{4}$ ，
特例4：（填写一个符合上述运算特征的例子）．
……

(2)、发现规律： $\sqrt{1 + \frac{1}{n^{2}} + \frac{1}{{(n + 1)}^{2}}} =$ ▲ （ $n$ 为正整数），并证明此规律成立．

(3)、应用规律：
①计算： $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} + ⋯ + \sqrt{1 + \frac{1}{8^{2}} + \frac{1}{9^{2}}} + \sqrt{1 + \frac{1}{9^{2}} + \frac{1}{1 0^{2}}}$ ；
②如果 $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + ⋯ + \sqrt{1 + \frac{1}{{(n - 2)}^{2}} + \frac{1}{{(n - 1)}^{2}}} + \sqrt{1 + \frac{1}{{(n - 1)}^{2}} + \frac{1}{n^{2}}} = n - \frac{1}{5}$ ，那么n＝ ▲ ．

查看试题解析
27. 已知，在△ABC中，∠BAC＝30°，点D在射线BC上，连接AD，∠CAD＝ $α$ ，点D关于直线AC的对称点为E，点E关于直线AB的对称点为F，直线EF分别交直线AC，AB于点M，N，连接AF，AE，CE．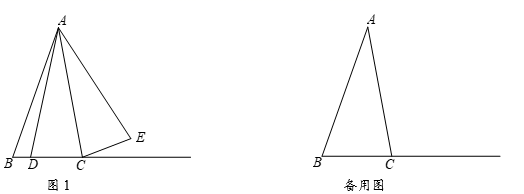

(1)、如图1，点D在线段BC上．
①根据题意补全图1；
②∠AEF ＝ ▲ （用含有 $α$ 的代数式表示），∠AMF＝ ▲ °；
③用等式表示线段MA，ME，MF之间的数量关系，并证明．

(2)、点D在线段BC的延长线上，且∠CAD＜60°，直接用等式表示线段MA，ME，MF之间的数量关系，不证明．

查看试题解析
28. 对于任意两个非零实数a，b，定义运算 $\otimes$ 如下： $a \otimes b = {\begin{array}{l} \frac{a}{b} (a > 0) \\ a + b (a < 0) \end{array}$ ．
如： $2 \otimes 3 = \frac{2}{3}$ ， $(- 2) \otimes 3 = - 2 + 3 = 1$ ．
根据上述定义，解决下列问题：

(1)、 $\sqrt{6} \otimes \sqrt{3} =$ ， $(- \sqrt{5}) \otimes \sqrt{5} =$ ；

(2)、如果 $(x^{2} + 1) \otimes (x^{2} - x) = 1$ ，那么x ＝；

(3)、如果 $(x^{2} - 3) \otimes x = (- 2) \otimes x$ ，求x的值．

查看试题解析