北京市大兴区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 飞沫一般认为是直径大于5微米（5微米＝0.000005米）的含水颗粒．飞沫传播是新型冠状病毒的主要传播途径之一，日常面对面说话、咳嗽、打喷嚏都可能造成飞沫传播．因此有效的预防措施是戴口罩并尽量与他人保持1米以上社交距离．将0.000005用科学记数法表示应为（）．

A、 $0.5 \times 1 0^{- 5}$ B、 $0.5 \times 1 0^{- 6}$ C、 $5 \times 1 0^{- 5}$ D、 $5 \times 1 0^{- 6}$

查看试题解析
2. 下列倡导节约的图案中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在代数式 $\frac{3}{2 + x}$ ， $\frac{3 + x}{2}$ ， $\frac{3}{2} + x$ ， $\frac{3 + x}{2 x}$ ， $\frac{x}{π}$ 中，分式的个数为（）．

A、2 B、3 C、4 D、5

查看试题解析
4. 下列运算正确的是（）．

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(- a^{3})}^{2} = a^{6}$ C、 ${(3 a)}^{3} = 9 a^{3}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
5. 下列因式分解正确的是（）．

A、 $2 a^{2} - 4 a = 2 (a^{2} + a)$ B、 $- a^{2} + 4 = (a + 2) (a - 2)$ C、 $a^{2} - 2 a + 1 = {(a - 1)}^{2}$ D、 $a^{2} - 10 a + 25 = a (a - 10) + 25$

查看试题解析
6. 若一个多边形的外角和与它的内角和相等，则这个多边形是（）

A、三角形 B、四边形 C、五边形 D、六边形

查看试题解析
7. 下列三个说法：
①有一个内角是30°，腰长是6的两个等腰三角形全等；②有一个内角是120°，底边长是3的两个等腰三角形全等；③有两条边长分别为5，12的两个直角三角形全等．
其中正确的个数有（）．

A、3 B、2 C、1 D、0

查看试题解析
8. 将一个长为2m，宽为 $2 n (m > n > 0)$ 的长方形纸片，用剪刀沿图1中虛线剪开，把它分成四块形状和大小都一样的小长方形纸片，然后按图2的方式拼成一个边长为 $(m + n)$ 的正方形，则图2中空白部分的小正方形面积是（）．

A、 $2 m n$ B、 ${(m + n)}^{2}$ C、 $m^{2} - n^{2}$ D、 ${(m - n)}^{2}$

查看试题解析

二、填空题

9. 若分式 $\frac{2}{x - 3}$ 有意义，则x的取值范围是

查看试题解析
10. 分解因式： $4 x^{2} - y^{2} =$ ．

查看试题解析
11. 若 $x^{2} + k x y + 4 y^{2}$ 是完全平方式，则k的值等于．

查看试题解析
12. 若 $a - 3 b = 0$ ，且 $a \neq 0$ ，则分式中 $\frac{a + b}{a - b}$ 的值为．

查看试题解析
13. 如图，在 $R t △ A B C$ 中， $∠ A = 90 °$ ， $∠ C = 30 °$ ， $A B = 2$ ， EF是AC的垂直平分线，P是直线EF上的任意一点，则 $P A + P B$ 的最小值是．

查看试题解析
14. 甲做360个零件与乙做480个零件所用的时间相同，已知两人每天共做140个零件，若设甲每天做x个零件，则可列方程．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ B = 30 °$ ， $∠ B A C = 120 °$ ， $A D ⊥ A C$ 交BC于点D．若 $A D = 3$ ，则 $B C =$ ．

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $D E ⊥ A B$ 交BC的延长线于点E，若 $A D = D E$ ，点C是BE中点，则 $∠ B =$ °．

查看试题解析

三、解答题

17. 计算： ${(- 3)}^{2} - {(π - 3)}^{0} + \sqrt{4} + {(\frac{1}{2})}^{- 1}$ ．

查看试题解析
18. 计算： $a^{3} \cdot a + {(- 3 a^{3})}^{2} \div a^{2}$ ．

查看试题解析
19. 已知 $x^{2} - x - 3 = 0$ ，求代数式 ${(x - 1)}^{2} + (x - 1) (2 x + 1)$ 的值．

查看试题解析
20. 计算： $\frac{a^{2} - 3 a}{a^{2} - 2 a + 1} \div \frac{a - 3}{a^{2} - 1} - \frac{a + 1}{a - 1}$ ．

查看试题解析
21. 解方程： $\frac{2 x - 3}{x^{2} - 1} - \frac{1}{x + 1} = \frac{2}{x - 1}$ ．

查看试题解析
22. 如图， $△ A B C$ ≌ $△ A D E$ ， AC和AE，AB和AD是对应边，点E在边BC上，AB与DE交于点F．

(1)、求证： $∠ C A E = ∠ B A D$ ；

(2)、若 $∠ B A D = 35 °$ ，求 $∠ B E D$ 的度数．

查看试题解析
23. 下面是小明同学设计的“已知底边及底边上的中线作等腰三角形”的尺规作图过程．
已知：如图1，线段a和线段b．
求作： $△ A B C$ ，使得 $A B = A C$ ， $B C = a$ ， BC边上的中线为b．
作法：如图2，
①作射线BM，并在射线BM上截取 $B C = a$ ；
②作线段BC的垂直平分线PQ，PQ交BC于点D；
③以点D为圆心，b为半径作弧，交PQ于点A；
④连接AB和AC．
则 $△ A B C$ 为所求作的等腰三角形．

(1)、用直尺和圆规，依作法补全图2中的图形（保留作图痕迹）；

(2)、完成下面的证明：
证明：由作图可知 $B C = a$ ， $A D = b$ ．
∵PQ为线段BC的垂直平分线，点A在PQ上，
∴ $A B = A C$ （ ▲ ）（填推理的依据）．
又∵线段BC的垂直平分线PQ交BC于点D，
∴ $B D = C D$ ．
∴AD为BC边上的中线．

查看试题解析
24. 如图，在 $△ A B C$ 中，AD平分 $∠ B A C$ ， $C E ⊥ A D$ 于点E．求证： $∠ A C E = ∠ B + ∠ E C D$ ．

查看试题解析
25. 如图， $△ A B C$ 为等边三角形，D是BC中点， $∠ A D E = 60 °$ ， CE是 $△ A B C$ 的外角 $∠ A C F$ 的平分线．
求证： $A D = D E$ ．

查看试题解析
26. 观察下列各式：
$(a + 1) (a^{2} - a + 1) = a^{3} + 1$ ；
$(a - 2) (a^{2} + 2 a + 4) = a^{3} - 8$ ；
$(3 a - 2) (9 a^{2} + 6 a + 4) = 27 a^{3} - 8$ ．

(1)、请你按照以上各式的运算规律，填空．
① $(x - 3) (x^{2} + 3 x + 9) =$ ；
② $(2 x + 1)$ （） $= 8 x^{3} + 1$ ；
③（） $(x^{2} + x y + y^{2}) = x^{3} - y^{3}$ ．

(2)、应用规律计算： $(a^{2} - b^{2}) (a^{2} + a b + b^{2}) (a^{2} - a b + b^{2})$ ．

查看试题解析
27. 在 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90 °$ ，点D是直线AC上一动点，连接BD并延长至点E，使 $E D = B D$ ．过点E作 $E F ⊥ A C$ 于点F．

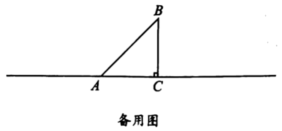(1)、如图1，当点D在线段AC上（点D不与点A和点C重合）时，此时DF与DC的数量关系是．

(2)、如图2，当点D在线段AC的延长线上时，依题意补全图形，并证明： $2 A D = A F + E F$ ．

(3)、当点D在线段CA的延长线上时，直接用等式表示线段AD，AF，EF之间的数量关系是．

查看试题解析
28. 在平面直角坐标系xOy中，对于点P给出如下定义：点P到图形 $G_{1}$ 上各点的最短距离为 $d_{1}$ ，点P到图形 $G_{2}$ 上各点的最短距离为 $d_{2}$ ，若 $d_{1} = d_{2}$ ，就称点P是图形 $G_{1}$ 和图形 $G_{2}$ 的一个“等距点”．
已知点 $A (6 ， 0)$ ， $B (0 ， 6)$ ．

(1)、在点 $D (- 6 ， 0)$ ， $E (3 ， 0)$ ， $F (0 ， 3)$ 中，是点A和点O的“等距点”；

(2)、在点 $G (- 2 ， - 1)$ ， $H (2 ， 2)$ ， $I (3 ， 6)$ 中，是线段OA和OB的“等距点”；

(3)、点 $C (m ， 0)$ 为x轴上一点，点P既是点A和点C的“等距点”，又是线段OA和OB的“等距点”．
①当 $m = 8$ 时，是否存在满足条件的点P，如果存在请求出满足条件的点P的坐标，如果不存在请说明理由；
②若点P在 $△ O A B$ 内，请直接写出满足条件的m的取值范围．

查看试题解析