北京市昌平区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、2 B、±2 C、16 D、±16

查看试题解析
2. 若分式 $ \frac{3 a}{a - 2}$ 有意义，则 $a$ 的取值范围是（）

A、a≠2 B、a≠0 C、a＜2 D、a≥2

查看试题解析
3. 下列垃圾分类的标识中，是轴对称图形的是（）

A、①② B、③④ C、①③ D、②④

查看试题解析
4. 分式 $ \frac{- a}{a - b}$ 可变形为（）

A、 $ \frac{a}{- a - b}$ B、 $ \frac{a}{a + b}$ C、 $- \frac{a}{a - b}$ D、 $- \frac{a}{a + b}$

查看试题解析
5. 下列命题是假命题的是（）

A、对顶角相等 B、直角三角形两锐角互余 C、同位角相等 D、全等三角形对应角相等

查看试题解析
6. 将一副三角尺按如图所示的方式摆放，则 $∠ α$ 的大小为（）

A、 $85 °$ B、 $75 °$ C、 $65 °$ D、 $60 °$

查看试题解析
7. 任意掷一枚骰子，下列事件中：①面朝上的点数小于1；②面朝上的点数大于1；③面朝上的点数大于0，是必然事件，不可能事件，随机事件的顺序是（）

A、①②③ B、①③② C、③②① D、③①②

查看试题解析
8. 如图，已知Rt△ABC中，∠C＝90°，∠A＝30°，在直线BC上取一点P，使得△PAB是等腰三角形，则符合条件的点P有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 若式子 $\sqrt{x - 3}$ 有意义，则实数 $x$ 的取值范围是.

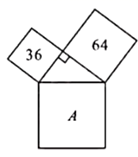
查看试题解析
10. 若分式 $\frac{x - 5}{2 x + 1}$ 的值为0，则x＝．

查看试题解析
11. 在一个不透明的袋中装有除颜色外其余均相同的5个红球和3个黄球，如果从中随机摸出一个，那么摸到黄球的可能性大小是．

查看试题解析
12. 如图，数字代表所在正方形的面积，则A所代表的正方形的面积为.

查看试题解析
13. 已知43²＝1849，44²＝1936，45²＝2025，46²＝2116，若n为整数且n＜ $\sqrt{2022}$ ＜n＋1，则n的值是．

查看试题解析
14. 实数 $m$ 在数轴上的位置如图所示，则化简 $\sqrt{m^{2}} + | m - 1 |$ 的结果为．

查看试题解析
15. 已知一张三角形纸片 $A B C ($ 如图甲 $)$ ，其中 $A B = A C .$ 将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为 $B D ($ 如图乙 $) .$ 再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为 $E F ($ 如图丙 $) .$ 原三角形纸片ABC中， $∠ A B C$ 的大小为 $^{\circ} .$

查看试题解析
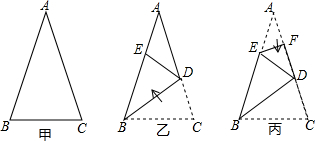16. 我们规定：如果实数a，b满足a＋b＝1，那么称a与b互为“匀称数”．

(1)、1－π与互为“匀称数”；

(2)、已知 $(m - 1) (1 + \sqrt{2}) = - 1$ ，那么m与互为“匀称数”．

查看试题解析

三、解答题

17. 计算： $\sqrt{\frac{1}{3}} \times \sqrt{12} - \sqrt{32} \div \sqrt{2}$ ．

查看试题解析
18. 计算： $\sqrt{8} + {(\sqrt{8})}^{2} + \sqrt{18} - \sqrt[3]{8}$ ．

查看试题解析
19. 如图，点B、F、C、E在一条直线上，BF＝EC，AC＝DF，AC∥DF．求证：∠A＝∠D．

查看试题解析
20. 计算： $\frac{a^{2}}{a - 1} + \frac{1}{1 - a} .$

查看试题解析
21. 解分式方程： $\frac{2 x}{x + 3}$ +1= $\frac{7}{2 x + 6}$ ．

查看试题解析
22. 列方程解应用题：同学们在计算机课上学打字．张帆比王凯每分钟多录入20个字，张帆录入300个字与王凯录入200个字的时间相同．问王凯每分钟录入多少个字．

查看试题解析
23. 如图，在△ABC中，∠C $=$ 90°．

(1)、用尺规作图，保留作图痕迹，不写作法：在边BC上求作一点D，使得点D到AB的距离等于DC的长；

(2)、在（1）的条件下，若AC＝6，AB＝10，求CD的长．

查看试题解析
24. 一个三角形三边长分别为a，b，c．

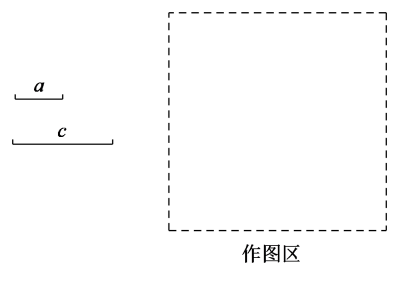(1)、当a＝3，b＝4时，
① c的取值范围是；
② 若这个三角形是直角三角形，则c的值是；

(2)、当三边长满足 $\frac{a + b + c}{3} = b$ 时，
① 若两边长为3和4，则第三边的值是 ▲ ；
② 在作图区内，尺规作图，保留作图痕迹，不写作法：已知两边长为a，c（a＜c），求作长度为b的线段（标注出相关线段的长度）．

查看试题解析
25. 若关于x的分式方程 $\frac{x}{x - 3} - 2 = \frac{m}{x - 3}$ 的解是正数，当m取最大整数时，求 $m^{2} + 2 m + 1$ 的平方根．

查看试题解析
26. 在等边三角形ABC中，点D是边AB的中点，过点D作DE∥BC交AC于点E，点F在BC边上，连接DF，EF．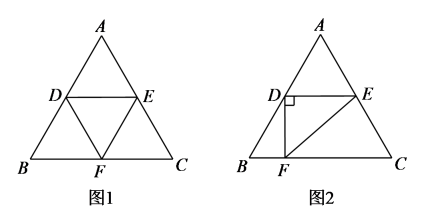

(1)、如图1，当DF是∠BDE的平分线时，若AE＝2，求EF的长；

(2)、如图2，当DF⊥DE时，设AE＝a，则EF的长为（用含a的式子表示）．

查看试题解析
27. 大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数．因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来，于是小燕用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分．理由是：对于正无理数，用本身减去其整数部分，差就是其小数部分．因为 $\sqrt{2}$ 的整数部分为1，所以 $\sqrt{2}$ 的小数部分为 $\sqrt{2} - 1$ ．
参考小燕同学的做法，解答下列问题：

(1)、写出 $\sqrt{13}$ 的小数部分为；

(2)、已知 $7 + \sqrt{7}$ 与 $7 - \sqrt{7}$ 的小数部分分别为a和b，求a²＋2ab＋b²的值；

(3)、如果 $\sqrt{9} + \sqrt[3]{9} = x + y$ ，其中x是整数，0＜y＜1，那么 $\frac{2}{5} x + y$ ＝

(4)、设无理数 $\sqrt{m}$ （m为正整数）的整数部分为n，那么 $m - \sqrt{m}$ 的小数部分为（用含m，n的式子表示）．

查看试题解析
28. 若△ABC和△ADE均为等腰三角形，且AB＝AC＝AD＝AE，当∠ABC和∠ADE互余时，称△ABC与△ADE互为“底余等腰三角形”，△ABC的边BC上的高AH叫做△ADE的“余高”．

(1)、如图1，△ABC与△ADE互为“底余等腰三角形”．
①若连接BD，CE，判断△ABD与△ACE是否互为“底余等腰三角形”：            ▲       （填“是”或“否”）；
②当∠BAC＝90°时，若△ADE的“余高”AH＝ $\sqrt{5}$ ，则DE＝            ▲       ；
③当0°＜∠BAC＜180°时，判断DE与AH之间的数量关系，并证明；

(2)、如图2，在四边形ABCD中，∠ABC＝60°，DA⊥BA，DC⊥BC，且DA＝DC．
①画出△OAB与△OCD，使它们互为“底余等腰三角形”；
②若△OCD的“余高”长为a，则点A到BC的距离为            ▲       （用含a的式子表示）．

查看试题解析