安徽省安庆市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 在平面直角坐标系中,点P(2,﹣3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列四个图形中,线段BE是△ABC的高的是( )A、
3. 下列四个图形中,线段BE是△ABC的高的是( )A、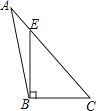 B、
B、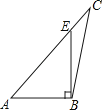 C、
C、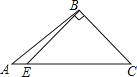 D、
D、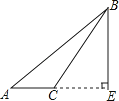 4. 如图在正方形网格中,若A(1,1),B(2,0),则C点的坐标为( )
4. 如图在正方形网格中,若A(1,1),B(2,0),则C点的坐标为( ) A、(-3,-2) B、(3,-2) C、(-2,-3) D、(2,-3)5. 将下列长度的三条线段首尾相连,其中能组成三角形的是( )A、5,6,10 B、2,5,8 C、4,5,9 D、3,4,86. 人字梯中间一般会设计一“拉杆”,你认为这样做的道理是( )
A、(-3,-2) B、(3,-2) C、(-2,-3) D、(2,-3)5. 将下列长度的三条线段首尾相连,其中能组成三角形的是( )A、5,6,10 B、2,5,8 C、4,5,9 D、3,4,86. 人字梯中间一般会设计一“拉杆”,你认为这样做的道理是( ) A、两点之间,线段最短 B、垂线段最短 C、三角形具有稳定性 D、两直线平行,内错角相等7. 若 有意义,则x的取值范围是A、 且 B、 C、 D、8. 如图,在Rt△ABC中,∠ACB=90º,∠A=60º,CD是斜边AB上的高,若AD=3cm,则斜边AB的长为( )
A、两点之间,线段最短 B、垂线段最短 C、三角形具有稳定性 D、两直线平行,内错角相等7. 若 有意义,则x的取值范围是A、 且 B、 C、 D、8. 如图,在Rt△ABC中,∠ACB=90º,∠A=60º,CD是斜边AB上的高,若AD=3cm,则斜边AB的长为( ) A、3cm B、6cm C、9cm D、12cm9. 如图,已知锐角∠AOB.在射线OA上取一点C,以点O为圆心,OC的长为半径作弧,交射线OB于点D,连结CD;分别以点C,D为圆心,CD的长为半径作弧,两弧在∠AOB内部交于点P,连结CP,DP;作射线OP,交CD于点Q.根据以上作图过程及所作图形,有下列结论①CP//OB;②∠AOP = ∠BOP;③OP⊥CD.其中正确的结论( )
A、3cm B、6cm C、9cm D、12cm9. 如图,已知锐角∠AOB.在射线OA上取一点C,以点O为圆心,OC的长为半径作弧,交射线OB于点D,连结CD;分别以点C,D为圆心,CD的长为半径作弧,两弧在∠AOB内部交于点P,连结CP,DP;作射线OP,交CD于点Q.根据以上作图过程及所作图形,有下列结论①CP//OB;②∠AOP = ∠BOP;③OP⊥CD.其中正确的结论( ) A、①②③ B、②③ C、①③ D、③10. 如图,点A的坐标为 , 点B是x轴正半轴上的动点,以AB为腰作等腰直角 , 使 , 设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A、①②③ B、②③ C、①③ D、③10. 如图,点A的坐标为 , 点B是x轴正半轴上的动点,以AB为腰作等腰直角 , 使 , 设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 将命题“直角三角形斜边上的中线等于斜边的一半”改写成“如果…那么…”的形式.12. 如图,在由6个相同的小正方形拼成的网格中,∠2﹣∠1=°.
 13. 在平面直角坐标系中,对于点和 , 给出如下定义:如果当时,;当时, . 那么称点Q为点P的“关联点”.例如点的“关联点”为 . 如果点是一次函数图象上点M的“关联点”,那么n的值为 .14. 如图,在四边形ABCD中,∠BCD=50°,∠B=∠D=90°,在BC、CD上分别取一点M、N,使△AMN的周长最小,则∠MAN=°.
13. 在平面直角坐标系中,对于点和 , 给出如下定义:如果当时,;当时, . 那么称点Q为点P的“关联点”.例如点的“关联点”为 . 如果点是一次函数图象上点M的“关联点”,那么n的值为 .14. 如图,在四边形ABCD中,∠BCD=50°,∠B=∠D=90°,在BC、CD上分别取一点M、N,使△AMN的周长最小,则∠MAN=°.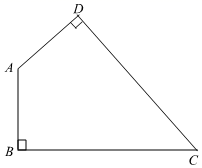
三、解答题
-
15. 如图,点B、C、D、F在一条直线上,FD=BC,DE=CA,EF=AB,求证:EF∥AB.
 16. 在平面直角坐标系中
16. 在平面直角坐标系中
⑴在图中描出 , , , 连接AB、BC、AC,得到 , 并将向右平移5个单位,再向上平移2个单位的得到;
⑵作出 , 使它与关于x轴对称.
17. 已知y与2x-1成正比例,当x=2时,y=6.(1)、求y与x之间的函数关系式;(2)、当y=-6时,求x的值.18. ∠ACD是△ABC的外角,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E. (1)、若∠A=58º,求:∠E的度数.(2)、猜想∠A与∠E的关系,并说明理由.19. 已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A.
(1)、若∠A=58º,求:∠E的度数.(2)、猜想∠A与∠E的关系,并说明理由.19. 已知:如图一次函数y1=﹣x﹣2与y2=x﹣4的图象相交于点A. (1)、求点A的坐标;(2)、若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.(3)、结合图象,直接写出y1≥y2时x的取值范围.20. 如图①,在 中, ,点D是 的中点,点E在 上.
(1)、求点A的坐标;(2)、若一次函数y1=﹣x﹣2与y2=x﹣4的图象与x轴分别相交于点B、C,求△ABC的面积.(3)、结合图象,直接写出y1≥y2时x的取值范围.20. 如图①,在 中, ,点D是 的中点,点E在 上.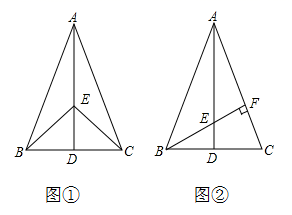 (1)、求证: ;(2)、如图②,若 的延长线交 于点F , 且 ,垂足为F , ,其他条件不变.求证: .21. 教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
(1)、求证: ;(2)、如图②,若 的延长线交 于点F , 且 ,垂足为F , ,其他条件不变.求证: .21. 教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
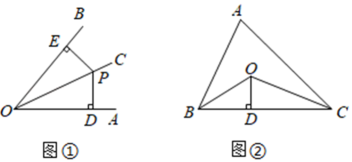 (1)、定理证明:请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.(2)、定理应用:如图②,△ABC的周长是10,BO、CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若OD=3,则△ABC的面积为 .22. 接种新冠病毒疫苗,建立全民免疫屏障,是战胜病毒的重要手段.北京科兴中维需运输一批疫苗到我市疾控中心,据调查得知,2辆 型冷链运输车与3辆 型冷链运输车一次可以运输600盒:5辆 型冷链运输车与6辆 型冷链运输车一次可以运输1350盒.(1)、求每辆 型车和每辆 型车一次可以分别运输多少盒疫苗.(2)、计划用两种冷链运输车共12辆运输这批疫苗, 型车一次需费用5000元, 型车一次需费用3000元.若运输物资不少于1500盒,且总费用小于54000元.请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?23. 在△ABC中,∠C=90°,AC=BC=2,将一块三角板的直角顶点放在斜边AB的中点P处,将此三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于点D、点E,图①,②,③是旋转得到的三种图形.
(1)、定理证明:请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.(2)、定理应用:如图②,△ABC的周长是10,BO、CO分别平分∠ABC和∠ACB,OD⊥BC于点D,若OD=3,则△ABC的面积为 .22. 接种新冠病毒疫苗,建立全民免疫屏障,是战胜病毒的重要手段.北京科兴中维需运输一批疫苗到我市疾控中心,据调查得知,2辆 型冷链运输车与3辆 型冷链运输车一次可以运输600盒:5辆 型冷链运输车与6辆 型冷链运输车一次可以运输1350盒.(1)、求每辆 型车和每辆 型车一次可以分别运输多少盒疫苗.(2)、计划用两种冷链运输车共12辆运输这批疫苗, 型车一次需费用5000元, 型车一次需费用3000元.若运输物资不少于1500盒,且总费用小于54000元.请你列出所有运输方案,并指出哪种方案所需费用最少,最少费用是多少?23. 在△ABC中,∠C=90°,AC=BC=2,将一块三角板的直角顶点放在斜边AB的中点P处,将此三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于点D、点E,图①,②,③是旋转得到的三种图形. (1)、观察线段PD和PE之间有怎样的大小关系?并以图②为例,并加以证明;(2)、观察线段CD、CE和BC之间有怎样的数量关系?并以图③为例,并加以证明;(3)、△PBE是否能成为等腰三角形?若能,求出∠PEB的度数;若不能,请说明理由.
(1)、观察线段PD和PE之间有怎样的大小关系?并以图②为例,并加以证明;(2)、观察线段CD、CE和BC之间有怎样的数量关系?并以图③为例,并加以证明;(3)、△PBE是否能成为等腰三角形?若能,求出∠PEB的度数;若不能,请说明理由.