天津市和平区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，可以看作是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 对于二次函数y＝﹣（x﹣1）²+4，下列说法错误的是（　　）

A、开口向下 B、当x>1时，y随x的增大而减小 C、函数图象与x轴交于点（﹣1，0）和（3，0） D、当x＝1时，y有最小值4

查看试题解析
3. 如图，两个等圆⊙O₁和⊙O₂相交于A、B两点，且⊙O₁经过⊙O₂的圆心，则∠O₁AB的度数为（　　）

A、45° B、30° C、20° D、15°

查看试题解析
4. 根据下列条件，判断△ABC与△A′B′C′能相似的条件有（　　）
①∠C＝∠C′＝90°，∠A＝25°，∠B′＝65°；
②∠C＝90°，AC＝6cm，BC＝4cm， $∠ C ＝ 90 °$ ， A′C′＝9cm，B′C′＝6cm；
③AB＝10cm，BC＝12cm，AC＝15cm，A′B′＝150cm，B′C′＝180cm，A′C′＝225cm；
④△ABC与△A′B′C′是有一个角为80°等腰三角形

A、1对 B、2对 C、3对 D、4对

查看试题解析
5. 如图，要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高，高度为3m，水柱落地处离池中心3m，水管的长为（）

A、 $\frac{9}{4} m$ B、 $\frac{19}{8} m$ C、 $\frac{39}{16} m$ D、 $\frac{45}{16} m$

查看试题解析
6. 如图，在△ABC中，AB＝AC，∠BAC＝50°，将△ABC绕着点A顺时针方向旋转得△ADE，AB，CE相交于点F，若AD∥CE时，则∠BAE的大小是（　　）

A、20° B、25° C、30° D、35°

查看试题解析
7. 把形状完全相同风景不同的两张图片全部从中剪断，再把四张形状相同的小图片混合在一起，从四张图片中随机摸取两张，则这两张小图片恰好合成一张完整图片的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{2}{3}$

查看试题解析
8. 如图，AB，BC，CD分别与⊙O相切于E、F、G三点，且AB $∥$ CD，BO＝3，CO＝4，则OF的长为（　　）

A、5 B、 $\frac{9}{5}$ C、 $\frac{16}{5}$ D、 $\frac{12}{5}$

查看试题解析
9. 如图，在平行四边形 $A B C D$ 中，F是 $A D$ 上一点，且 $A F = 2 F D$ ，连结 $B F$ 并延长交 $C D$ 的延长线于点G ，则 $\frac{B E}{E G}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{4}$

查看试题解析
10. 已知二次函数y＝ax²+bx+c（a≠0，a，b，c为常数），如果a＞b＞c，且a+b+c＝0，则它的图象可能是（　　）

A、 B、 C、 D、

查看试题解析
11. 如图，在平面直角坐标系中，△ABC的顶点A在第二象限，点B坐标为（﹣2，0），点C坐标为（﹣1，0），以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C．若点A的对应点A′的坐标为（2，﹣3），点B的对应点B′的坐标为（1，0），则点A坐标为（　　）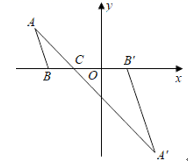

A、（﹣3，﹣2） B、（﹣2， $\frac{3}{2}$ ） C、（﹣ $\frac{5}{2}$ ， $\frac{3}{2}$ ） D、（﹣ $\frac{5}{2}$ ， 2）

查看试题解析
12. 已知二次函数y＝﹣（x﹣m）²﹣m+1（m为常数）．
①二次函数图象的顶点始终在直线y＝﹣x+1上
②当x＜2时，y随x的增大而增大，则m=2
③点A（x₁ ， y₁）与点B（x₂ ， y₂）在函数图象上，若x₁＜x₂ ， x₁+x₂＞2m，则y₁＜y₂
其中，正确结论的个数是（     ）

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

13. 已知正六边形的周长是24，则这个正六边形的半径为．

查看试题解析
14. 一个质地均匀的小正方体，六个面分别标有数字“1”、“2”、“3”、“4”、“5”、“6”，掷一次小正方体后，观察朝上一面的数字出现偶数的概率是．

查看试题解析
15. 用一个圆心角为120°，半径为6的扇形作一个圆锥的侧面，这个圆锥的底面圆的半径是．

查看试题解析
16. 如图，等腰直角三角形ABC，∠C=90°，AC=BC=4，M为AB的中点，∠PMQ=45°，∠PMQ的两边分别交BC于点P，交AC于点Q，若BP=3，则AQ= ．

查看试题解析
17. 已知抛物线 $y = x^{2} - 2 b x + 2 b^{2} - 4 c$ （其中b，c为常数）经过不同两点 $A (1 - b ， m)$ ， $B (2 b + c ， m)$ ，且该二次函数的图象与x轴有公共点，则 $b + c$ 的值为．

查看试题解析

三、解答题

18. 如图

(1)、如图①，AB，CD是⊙O的两条平行弦，OE⊥CD交⊙O于点E，则弧AC弧BD（填“>”，“<”或“=”）；

(2)、如图②，△PAB是⊙O的内接三角形，OE⊥AB交⊙O于点E，则∠APE∠BPE（填“>”，“<”或“=”）；

(3)、如图③，△PAB是⊙O的内接三角形，∠QPA是它的外角，在弧AP上有一点G，满足PG平分∠QPA，请用无刻度的直尺，画出线段PG．（不要求证明）

查看试题解析
19.

(1)、解一元二次方程：x²﹣6x+9＝（5﹣2x）²；

(2)、求证：无论m取何值时，方程（x﹣3）（x﹣2）﹣m²＝0总有两个不相等的实数根．

查看试题解析
20. 已知AB是⊙O的直径，点C在⊙O上，D为弧BC的中点．

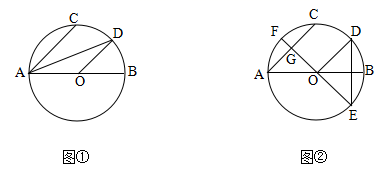(1)、如图①，连接AC，AD，OD，求证：OD $∥$ AC；

(2)、如图②，过点D作DE⊥AB交⊙O于点E，直径EF交AC于点G，若G为AC的中点，⊙O的半径为2，求AC的长．

查看试题解析
21. 已知AB是⊙O直径，点C为⊙O上一点，过点C作⊙O的切线PC交AB的延长线于点P，D为弧AC上一点，连接BD，BC，DC．

(1)、如图①，若∠D=26°，求∠PCB的大小；

(2)、如图②，若四边形CDBP为平行四边形，求∠PCB，∠ADC的大小．

查看试题解析
22. 如图，在△ABC中，∠B＝90°，AB＝12cm，BC＝24cm，动点P从点A开始沿边AB向点B以2cm/s的速度移动，动点Q从点B开始沿边BC向点C以4cm/s的速度移动，如果P、Q两点分别从A，B两点
同时出发，设运动时间为 $t$ s．

(1)、用含t的式子表示：
AP＝cm，BP＝cm，BQ＝cm， ${S_{△}}_{P B Q} =$ cm² ， $S_{四边形 A P Q C} =$ cm²；

(2)、当△PBQ的面积为32cm²时，求运动时间；

(3)、四边形APQC的面积能否等于72cm²？若能，求出运动的时间；若不能，说明理由．

查看试题解析
23. 九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销售量的相关信息如下表：

时间x（天）

1≤x＜50

50≤x≤90

售价（元/件）

x＋40

90

每天销量（件）

200－2x

已知该商品的进价为每件30元，设销售该商品的每天利润为y元[

(1)、求出y与x的函数关系式；

(2)、问销售该商品第几天时，当天销售利润最大，最大利润是多少？

(3)、该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果.

查看试题解析
24.

(1)、如图①，△PAM是等边三角形，在边PM上取点B（点B不与点P，M重合），连接AB，将线段AB绕点A逆时针旋转60°，得到线段AC，连接BC，MC．
①△MAC可以看作△PAB绕点逆时针旋转（度）得到的；

②∠PMC=（度）．

(2)、如图②，△PAM是等腰三角形，∠PAM=90°，AP=AM= $2 \sqrt{2}$ ，在边PM上取点B（点B不与点P，M重合），连接AB，将线段AB绕点A旋转，得到线段AC，旋转角为α，连接PC，BC．
①当α = 90°时，若△PBC的面积为1.5，求PB的长；

②若AB= $\sqrt{5}$ ，求△PBC面积的最大值（直接写出结果即可）．

查看试题解析
25. 已知抛物线 $y = x^{2} - (m + 1) x + 2 m + 3$ （m为常数），点A（-1，-1），B（3，7）．

(1)、当抛物线 $y = x^{2} - (m + 1) x + 2 m + 3$ 经过点A时，求抛物线解析式和顶点坐标；

(2)、抛物线的顶点随着m的变化而移动，当顶点移动到最高处时，
①求抛物线的解析式；
②在直线AB下方的抛物线上有一点E，过点E作EF⊥x轴，交直线AB于点F，求线段EF取最大值时的点E的坐标；

(3)、若抛物线与线段AB只有一个交点，求m的取值范围．

查看试题解析

时间x（天）	1≤x＜50	50≤x≤90
售价（元/件）	x＋40	90
每天销量（件）	200－2x