上海市长宁区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 已知在 中, , 那么 的长为( )A、 B、 C、 D、2. 如果向量 与向量 方向相反, 且 , 那么向量 用向量 表示为( )A、 B、 C、 D、3. 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长等于( )
 A、2 B、4 C、 D、4. 抛物线 (其中 ) 一定不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列命题中, 说法正确的是( )A、所有菱形都相似 B、两边对应成比例且有一组角对应相等的两个三角形相似 C、三角形的重心到一个顶点的距离, 等于它到这个顶点对边距离的两倍 D、斜边和直角边对应成比例, 两个直角三角形相似6. 如图, 点 E 是线段 的中点, , 下列结论中, 说法错误的是( )
A、2 B、4 C、 D、4. 抛物线 (其中 ) 一定不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列命题中, 说法正确的是( )A、所有菱形都相似 B、两边对应成比例且有一组角对应相等的两个三角形相似 C、三角形的重心到一个顶点的距离, 等于它到这个顶点对边距离的两倍 D、斜边和直角边对应成比例, 两个直角三角形相似6. 如图, 点 E 是线段 的中点, , 下列结论中, 说法错误的是( )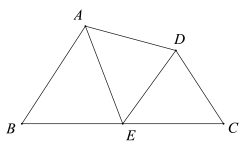 A、 与 相似 B、 与 相似 C、 D、
A、 与 相似 B、 与 相似 C、 D、二、填空题
-
7. 已知 , 那么 的值为 .8. 抛物线 的顶点坐标是 .9. 在比例尺为1:10000的地图上,相距5厘米的两地A、B的实际距离为米.10. 已知点 C 是线段 的黄金分割点, 㓚果 , 则 .11. 如果两个相似三角形周长之比为 , 那么这两个三角形的面积之比为 .12. 点 G 是 的重心, 过点 G 作 边的平行线与 边交于点 E 与 边交于点 F, 则 .13. 如图, 小明沿着坡度 的坡面由 B 到 A 直行走了 13 米时, 他上升的高度 米.
 14. 已知抛物线与y轴交于点A,过点A作x轴的平行线交抛物线于点B,若 , 则点B坐标为 .15. 我国古代数学著作 《九章算术》中记载:“今有邑方不知大小, 各中开门.出北门三十步有木,出西门七百五十步有木.问邑方几何?”示意图如图,正方形中,分别是和的中点,若 , 且过点A,那么正方形的边长为 .
14. 已知抛物线与y轴交于点A,过点A作x轴的平行线交抛物线于点B,若 , 则点B坐标为 .15. 我国古代数学著作 《九章算术》中记载:“今有邑方不知大小, 各中开门.出北门三十步有木,出西门七百五十步有木.问邑方几何?”示意图如图,正方形中,分别是和的中点,若 , 且过点A,那么正方形的边长为 . 16. 如图,在中,是斜边上的中线,点E是直线左侧一点,联结 , 若 , 则的值为 .
16. 如图,在中,是斜边上的中线,点E是直线左侧一点,联结 , 若 , 则的值为 . 17. 定义: 在 中, 点 D 和点 E 分别在 边、 边上, 且DE//BC,点 D 点 E 之间距离与直线 与直线 间的距离之比称为 关于 的横纵比. 已知, 在 中, 上的高长为 关于 的横纵比为 , 则 .18. 如图, 在 中, , 点 分别在 边和 边上,沿着直线 翻折 , 点 A 落在 边上,记为点 F,如果 , 则 .
17. 定义: 在 中, 点 D 和点 E 分别在 边、 边上, 且DE//BC,点 D 点 E 之间距离与直线 与直线 间的距离之比称为 关于 的横纵比. 已知, 在 中, 上的高长为 关于 的横纵比为 , 则 .18. 如图, 在 中, , 点 分别在 边和 边上,沿着直线 翻折 , 点 A 落在 边上,记为点 F,如果 , 则 .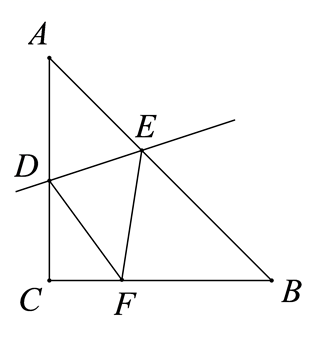
三、解答题
-
19. 计算:.20. 抛物线 经过点 .(1)、求抛物线的表达式及其顶点坐标;(2)、填空:如果将该拋物线平移, 使它的顶点移到点A的位置, 那么其平移的过程是平移后的抛物线表达式是 .21. 如图, 在梯形 中,AB//CD,且 , 点 E 是边 的中点, 联结 交对角线 于点 F, 若 .
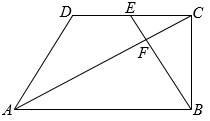 (1)、用 表示 ;(2)、求作 在 方向上的分向量.
(1)、用 表示 ;(2)、求作 在 方向上的分向量.(不要求写作法, 但要保留作图痕迹, 并指出所作图中表示结论的分向量)
22. 如图,某种路灯灯柱 垂直于地面,与灯杆 相连. 已知直线 与直线 的夹角是 .在地面点D处测得点A的仰角是 , 点B仰角是 , 点 A 与点D之间的距离为米.

求:
(1)、点 A 到地面的距离;(2)、 的长度.(精确到 米)(参考数据: )
23. 如图, 线段是的角平分线, 点E点 F 分别在线段 的延长线上, 联结 , 且 . (1)、求证: ;(2)、如果 , 求证: .
(1)、求证: ;(2)、如果 , 求证: .