辽宁省营口市大石桥市2021-2022学年九年级上学期期末考试数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下面是利用图形变化的知识设计的一些美丽的图案，其中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 关于x的一元二次方程2x²＋5x﹣1＝0根的说法，正确的是（）

A、方程没有实数根 B、方程有两个相等实数根 C、方程有两个不相等实数根 D、方程有一个实数根

查看试题解析
3. 下列说法错误的是（）

A、必然事件发生的概率是1 B、通过大量重复试验，可以用频率估计概率 C、概率很小的事件不可能发生 D、投一枚图钉，“钉尖朝上”的概率不能用列举法求得

查看试题解析
4. ①三点确定一个圆；②平分弦的直径平分弦所对的弧；③同圆或等圆中，相等的弦所对的圆心角相等；④在半径为4的圆中，30°的圆心角所对的弧长为 $\frac{π}{3}$ ；从上述4个命题中任取一个，是真命题的概率是（）

A、1 B、 $\frac{3}{4}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
5. 已知⊙O的半径为5cm，点P在⊙O外，则OP的长（）

A、小于5cm B、大于5cm C、小于10cm D、不大于10cm

查看试题解析
6. 如图，点 $O$ 为 $△ A B C$ 的内心， $∠ A = 60 °$ ， $O B = 2$ ， $O C = 4$ ，则 $△ O B C$ 的面积是（）

A、 $4 \sqrt{3}$ B、 $2 \sqrt{3}$ C、2 D、4

查看试题解析
7. 关于x的函数 $y = (a - 2) x^{2} + 2 x - 1$ 与x轴有交点，则a的取值范围是（）

A、 $a \geq 1$ B、 $a > 1$ C、 $a > 1$ 且 $a \neq 2$ D、 $a \geq 1$ 且 $a \neq 2$

查看试题解析
8. 如图，在长为32米、宽为20米的矩形地面是修筑同样宽的道路（图中阴影部分），余下部分种植草坪，要使草坪的面积为540平方米，设道路的宽为x米，则可列方程为（）

A、32×20﹣32x﹣20x＝540 B、（32﹣x）（20﹣x）+x²＝540 C、32x+20x＝540 D、（32﹣x）（20﹣x）＝540

查看试题解析
9. 如图，AB是⊙O的直径，弦CD⊥AB于点E，连接AD，若AB＝10，CD＝8，则AD的长为（）

A、8 B、2 $\sqrt{41}$ C、3 $\sqrt{10}$ D、4 $\sqrt{5}$

查看试题解析
10. 如图所示是抛物线y＝ax²+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：①a﹣b+c＞0；②3a+c＞0；③b²＝4a（c﹣n）；④一元二次方程ax²+bx+c＝n+1没有实数根.其中正确的结论个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若关于x的一元二次方程（k﹣1）x²﹣4x﹣1＝0有两个不相等的实数根，则k的取值范围是．

查看试题解析
12. 已知A（ $- \frac{1}{2}$ ， $y_{1}$ ），B（1， $y_{2}$ ），C（4， $y_{3}$ ）三点都在二次函数 $y = - {(x - 2)}^{2} + k$ 的图象上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系为．

查看试题解析
13. 若点P（m， $- m + 3$ ）关于原点的对称点Q在第三象限，那么m的取值范围是．

查看试题解析
14. 真实惠举行抽奖活动，在一个封闭的盒子里有400张形状一模一样的纸片，其中有20张是一等奖，摸到二等奖的概率是10％，摸到三等奖的概率是20%，剩下是“谢谢惠顾”，则盒子中有“谢谢惠顾”张．

查看试题解析
15. 已知 $x = \frac{- 3 + \sqrt{5}}{2}$ ，那么 $2 x^{2} + 6 x - 3$ 的值是．

查看试题解析
16. 如图，AB为圆O的切线，点A为切点，OB交圆O于点C，点D在圆O上，连接AD、CD、OA，若∠ADC=25°，则∠B的度数为．

查看试题解析
17. 如图Rt△ABC，∠C＝90°，分别以各边为直径作半圆，图中阴影部分在数学史上称为“希波克拉底月牙”：当AC＝6，BC＝8时，则阴影部分的面积为．

查看试题解析
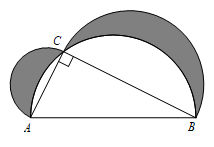18. 在△ABC中，∠BAC=60°，∠ABC=45°，AB=2，D是线段BC上的一个动点，以AD为直径画⊙O 分别交AB、AC于E、F，连接EF，则线段EF长度的最小值是．

查看试题解析

三、解答题

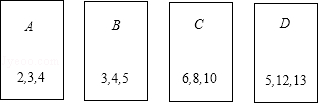
19. 解下列方程：

(1)、x²+2x-19=0；

(2)、(x+1)(2x-3)=2．

查看试题解析
20. 某食品零售店为食品厂代销一种盒装食品，当这种食品的单价定为7元时，每天卖出160盒，在此基础上，单价每提高1元，每天就会少卖20盒．若该食品每盒的成本为5元．设这种食品的单价为每盒 $x (x > 7)$ 元，零售店每天销售所获得的利润为y元．

(1)、求y与x之间的函数关系式并写出自变量x的取值范围；

(2)、当食品单价定为多少时，该零售店每天销售获得的利润最大？最大利润是多少？

查看试题解析
21. 在四张编号为A，B，C，D的卡片（除编号外，其余完全相同）的正面分别写上如图所示正整数后，背面朝上，洗匀放好，现从中随机抽取一张，不放回，再从剩下的卡片中随机抽取一张.

(1)、请用树状图或列表的方法表示两次抽取卡片的所有可能出现的结果（卡片用A，B，C，D表示）；

(2)、我们知道，满足a²+b²＝c²的三个正整数a，b，c成为勾股数，求抽到的两张卡片上的数都是勾股数的概率.

查看试题解析
22. 如图，AB是⊙O的直径，AD平分∠BAC，交⊙O于点D，过点D作直线DE⊥AC，交AC的延长线于点E，交AB的延长线于点F．

(1)、求证：EF是⊙O的切线；

(2)、若∠BAC＝60°，⊙O的半径为6，过点O作OH⊥AD，交AD于点H，求AH的长度．

查看试题解析
23. △ABC和△ADE均为等腰直角三角形，∠BAC＝∠DAE＝90°，将△ADE绕点A逆时针旋转一周，连接DB，将线段DB绕点D逆时针旋转90°得DF，连接EF．

(1)、如图1，当D在AC边上时，线段CD与EF的关系是，

(2)、如图2，当D在△ABC的内部时，（1）的结论是否成立？说明理由；

(3)、当AB＝3，AD＝ $\sqrt{2}$ ， ∠DAC＝ 45°时，直接写出△DEF的面积．

查看试题解析
24. 如图，在平面直角坐标系中，抛物线y＝﹣ $\frac{2}{3} x^{2} + \frac{4}{3} x + 2$ 交x轴于A ， B两点（A在B的左侧），交y轴于点C ．

(1)、求直线BC的解析式；

(2)、求抛物线的顶点及对称轴；

(3)、若点Q是抛物线对称轴上的一动点，线段AQ+CQ是否存在最小值？若存在，求出点Q的坐标；若不存在，说明理由；

(4)、若点P是直线BC上方抛物线上的一个动点，△PBC的面积是否存在最大值？若存在，求出点P的坐标及此时△PBC的面积；若不存在，说明理由．

查看试题解析