辽宁省沈阳市沈河区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $\frac{a}{b} = \frac{3}{2}$ ，那么下列等式中正确的是（）

A、 $\frac{a + b}{b} = \frac{5}{3}$ B、 $\frac{a - b}{b} = \frac{1}{3}$ C、 $2 a = 3 b$ D、 $\frac{a}{2} = \frac{b}{3}$

查看试题解析
2. 如图所示的几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
3. 在一个不透明的袋子里装有红球、黄球共20个，这些球除颜色外都相同．小明每次摸一个后放回再摸，通过多次试验发现，摸出红球的频率稳定在 $0.4$ 左右，则袋子中红球的个数最有可能是（）

A、8 B、5 C、12 D、15

查看试题解析
4. 下列命题中，真命题是（　　）

A、所有的平行四边形都相似 B、所有的矩形都相似 C、所有的菱形都相似 D、所有的正方形都相似

查看试题解析
5. 在一次篮球邀请赛中，参赛的每两个队之间都要赛一场，共赛45场，设共有x个队参赛、根据题意可列方程为（）

A、 $\frac{x (x - 1)}{2} = 45$ B、x（x﹣1）＝45 C、 $\frac{x (x + 1)}{2} = 45$ D、x（x+1）＝45

查看试题解析
6. 若两个相似三角形的周长比为1:3，则它们的面积比为（）

A、1:9 B、1:6 C、1:3 D、6:1

查看试题解析
7. 对于反比例函数 $y = - \frac{2021}{x}$ ，下列说法正确的是（）

A、图象分布在第一、三象限内 B、图象经过点（1，2021） C、当x＞0时，y随x的增大而增大 D、若点A（x₁、y₁），B（x₂ ， y₂）都在该函数的图象上，且x₁＜x₂ ，则y₁＞y₂

查看试题解析
8. 如图，四边形ABCD是平行四边形，下列结论中错误的是（）

A、当▱ABCD是矩形时，∠ABC＝90° B、当▱ABCD是菱形时，AC⊥BD C、当▱ABCD是正方形时，AC＝BD D、当▱ABCD是菱形时，AB＝AC

查看试题解析
9. 如图， $△ A B C$ 中， $∠ A = 76 ° ， A B = 8 ， A C = 6$ ．将 $△ A B C$ 沿图示中的虚线剪开．剪下的阴影三角形与原三角形不相似的是（）

A、 B、 C、 D、

查看试题解析
10. 如图，二次函数y＝ax²+bx+c（a≠0）的图象与x轴交于A，B两点，与y轴交于点C，且对称轴为直线x＝1，点B坐标为（﹣1，0）．则下面的四个结论：
①4a﹣2b+c＞0；②2a+b＝0；③当y＜0时，﹣1＜x＜3；④若m是实数，且m≠1，则a（m²﹣1）+bm＜b．其中正确的是（）

A、①② B、①③ C、②③ D、②④

查看试题解析

二、填空题

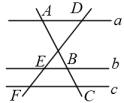
11. 方程x（x﹣3）=0的解为．

查看试题解析
12. 在平面直角坐标系xOy中，已知点A（﹣1，3），B（﹣6，3），以原点O为位似中心，在同一象限内把线段AB缩短为原来的 $\frac{1}{3}$ ，得到线段CD，其中点C对应点A，点D对应点B，则点D的坐标为．

查看试题解析
13. 如图，直线 $a ∥ b ∥ c$ ，直线AC，DF被直线a，b，c所截，若AB＝6，BC＝2，DF＝10，则EF的长为．

查看试题解析
14. 某校准备从A，B两名女生和C，D两名男生中任选2人代表学校参加沈阳市初中生辩论赛，则所选代表恰好为1名女生和1名男生的概率是．

查看试题解析
15. 关于x的一元二次方程kx²+3x﹣1＝0有实数根，则k的取值范围是.

查看试题解析
16. 如图，在矩形ABCD中，AD＝3，点E在AB边上，AE＝4，BE＝2，点F是AC上的一个动点．连接EF，将线段EF绕点E逆时针旋转90°并延长至其2倍，得到线段EG，当 $t a n ∠ G E A = \frac{1}{5}$ 时，点G到CD的距离是．

查看试题解析

三、解答题

17. 计算：2sin30°﹣3tan45°•sin²45°+cos60°．

查看试题解析
18. 如图是甲、乙两个可以自由转动且质地均匀的转盘，甲转盘被分成三个大小相同的扇形，分别标有1，2，3；乙转盘被分成四个大小相同的扇形，分别标有1，2，3，4，指针的位置固定，转动转盘直至它自动停止（若指针正好指向扇形的边界，则重新旋转转盘，直至指针指向扇形内部）．

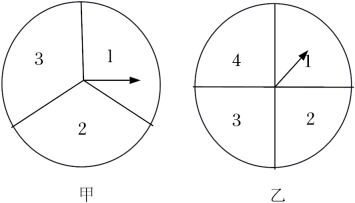(1)、转动甲转盘，指针指向3的概率是；

(2)、利用列表或画树状图的方法求转动两个转盘指针指向的两个数字和是5的概率．

查看试题解析
19. 如图，在Rt△ABC中，∠ACB＝90°，D为AB中点， $B E ∥ C D ， C E ∥ A B$ ．

(1)、试判断四边形BDCE的形状，并证明你的结论；

(2)、若∠ABC＝30°，AB＝4，则四边形BDCE的面积为．

查看试题解析
20. 据国家统计局统计数据显示，我国快递业务收入逐年增加.2018年我国某快递公司快递业务收入为300亿元，2020年增长至432亿元．假设该快递公司快递业务收入每年增长率都相同．

(1)、求该快递公司2018年至2020年快递业务收入的年平均增长率；

(2)、根据（1）的计算结果预测2021年该快递公司快递业务的收入为亿元．

查看试题解析
21. 如图是我们日常生活中经常使用的订书器，AB是订书机的托板，压柄BC绕着点B旋转，连接杆DE的一端点D固定，点E从A向B处滑动．在滑动过程中，DE的长保持不变．已知BD＝ $4 \sqrt{2}$ cm．

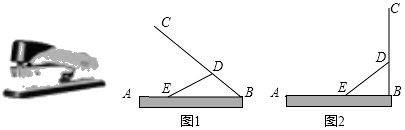(1)、如图1，当∠ABC＝45°，BE＝12cm时，求连接杆DE的长度；（结果保留根号）

(2)、现将压柄BC从图1的位置旋转到与底座AB垂直，如图2所示，请直接写出此过程中，点E滑动的距离．（结果保根号）

查看试题解析
22. 某超市销售一批日用品，每个进价为10元，经市场调研发现：该日用品每个售价为15元时，每天的销售量为200个，销售单价每提高1元，销售量就会减少8个，设销售单价为x（元），每天的销售量为y（个），每天的销售利润为W（元）．

(1)、直接写出销售量y与销售单价x之间的函数关系式；

(2)、求当销售单价x定为多少元时，每天销售利润W最大？最大利润是多少元？

(3)、若每天获得的利润不低于1288元，请直接写出销售单价x的取值范围．

查看试题解析
23. 如图，在平面直角坐标系xOy中，正方形ABCD的边AB在x轴的正半轴上，顶点C，D在第一象限内，正比例函数y₁＝3x的图象经过点D，反比例函数 $y_{2} = \frac{k}{x} (x > 0)$ 的图象经过点D，且与边BC交于点E，连接OE，已知AB＝3．

(1)、点D的坐标是；

(2)、求tan∠EOB的值；

(3)、观察图象，请直接写出满足y₂＞3的x的取值范围；

(4)、连接DE，在x轴上取一点P，使 $S_{△ D P E} = \frac{9}{8}$ ，过点P作PQ垂直x轴，交双曲线于点Q，请直接写出线段PQ的长．

查看试题解析
24.

(1)、（教材呈现）
如图1，在同一平面内，将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC＝∠G＝90°，BC＝6，若△ABC固定不动，将△AFG绕点A旋转，边AF、AG与边BC分别交于点D，E（点D不与点B重合，点E不与点C重合）
①求证：AE²＝DE•BE；
②求BE•CD的值；

(2)、（拓展探究）
如图2，在△ABC中，∠C＝90°，点D，E在边BC上，∠B＝∠DAE＝30°，且 $A D = \frac{3}{4} A E$ ，请直接写出 $\frac{D E}{B C}$ 的值．

查看试题解析
25. 如图，在平面直角坐标系xOy中，抛物线y＝ax²+2x+c（a≠0）与x轴交于点A（﹣1，0）和点B，交y轴于点C（0，3），顶点为D．

(1)、求抛物线解析式；

(2)、点E为线段BD上的一个动点，作EF⊥x轴于点F，连接OE，当△OEF面积最大时．求点E的坐标；

(3)、G是第四象限内抛物线上一点，过点G作GH⊥x轴于点H，交直线BD于点K、且 $O H = \frac{14}{5} G K$ ，作直线AG．
①点G的坐标是；
②P为直线AG上方抛物线上一点，过点P作PQ⊥AG于点Q，取点 $M (0 ， \frac{7}{4})$ ，点N为平面内一点，若四边形MPNQ是菱形，请直接写出菱形的边长．

查看试题解析