辽宁省鞍山市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图形中既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知关于x的一元二次方程 $3 x^{2} + (m + 3) x + m = 0$ 总有两个不相等的实数根，则m的取值范围是（）

A、 $m \geq 3$ B、 $m \neq 3$ C、 $m > 3$ 且 $m \neq 0$ D、 $m > 3$

查看试题解析
3. 如图，将 $△ O A B$ 绕点O逆时针旋转55°得到 $△ O C D$ ，若 $∠ A O B = 20 °$ ，则 $∠ B O C$ 的度数是（）

A、25° B、30° C、35° D、75°

查看试题解析
4. 将抛物线 $y = 2 {(x - 1)}^{2}$ 向右平移2个单位，向下平移3个单位得到的抛物线解析式是（）

A、 $y = 2 {(x - 3)}^{2} + 3$ B、 $y = 2 {(x - 3)}^{2} - 3$ C、 $y = 2 {(x + 1)}^{2} + 3$ D、 $y = 2 {(x + 1)}^{2} - 3$

查看试题解析
5. 已知，在圆中圆心角度数为45°，半径为10，则这个圆心角所对的扇形面积为（）

A、 $\frac{5}{2} π$ B、 $5 π$ C、 $10 π$ D、 $\frac{25}{2} π$

查看试题解析
6. 已知，点 $A (3 ， y_{1})$ ， $B (0 ， y_{2})$ ， $C (- 1 ， y_{3})$ 在二次函数 $y = x^{2} + 2 x + c$ 图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{3} < y_{2}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{1} < y_{2} < y_{3}$ D、 $y_{2} < y_{1} < y_{3}$

查看试题解析
7. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象经过点 $(1 ， - 1)$ ，且图象对称轴为直线 $x = 2$ ，则方程 $a x^{2} + b x + c = - 1 (a \neq 0)$ 的解为（）

A、 $x = 1$ B、 $x = 1$ ， $x = 2$ C、 $x = 2$ ， $x = 3$ D、 $x = 1$ ， $x = 3$

查看试题解析
8. 如图，在 $△ A B C$ 中， $A B = A C$ ，点D为 $B C$ 边上一点，将 $△ A B D$ 沿直线 $A D$ 翻折得到 $△ A B D$ ， $A B$ 与 $B C$ 边交于点E，若 $A B = 3 B D$ ，点 $E$ 为 $C D$ 中点， $B C = 6$ ，则 $A B$ 的长为（）

A、 $\frac{45}{7}$ B、6 C、 $\frac{45}{4}$ D、 $\frac{15}{2}$

查看试题解析

二、填空题

9. 方程 $x^{2} + 2 x = 0$ 的根是．

查看试题解析
10. 在平面直角坐标系 $x O y$ 中，以原点O为位似中心，作 $△ A B C$ 的位似图形，使它与 $△ A B C$ 相似比为2，若点A的坐标为 $(4 ， 2)$ ，则位似图形上与点A对应的点的坐标为．

查看试题解析
11. 某工厂生产一款零件的成本为500元，经过两年的技术创新，现在生产这款零件的成本为405元，求该款零件成本平均每年的下降率是多少？设该款零件成本平均每年的下降率为x，可列方程为．

查看试题解析
12. 如图， $⊙ O$ 为 $△ A B P$ 的外接圆， $A B = 2$ ， $∠ A P B = 30 °$ ，则 $⊙ O$ 直径长为．

查看试题解析
13. 《九章算术》是中国古代的数学专著，书中记载了这样一个问题：“今有句五步，股十二步．问句中容方几何．”其大意是：如图，Rt $△ A B C$ 的两条直角边的长分别为5和12，则它的内接正方形CDEF的边长为．

查看试题解析
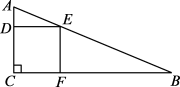14. 如图，A，B两点在x轴上，点P为反比例函数 $y = \frac{k}{x} (k > 0)$ 图象上一点，连接 $P O$ ， $P A$ ， $P B$ ，且 $P B$ 与反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象交于点N，若 $P A = P O$ ， $P N = B N$ ， $△ P A B$ 的面积为2，则k的值为．

查看试题解析
15. 如图，在正方形 $A B C D$ 中，点E为 $C D$ 边中点，连接 $A E$ ， $A E$ 与对角线 $B D$ 交于点F，连接 $C F$ ， $B E$ ，且 $C F$ 与 $B E$ 交于点H，连接 $D H$ ，则下列结论：① $B E ⊥ C F$ ；② $\frac{F H}{E H} = \frac{4}{3}$ ；③ $D H^{2} = C H \cdot B H$ ；④ $△ E H D ∽ △ F D C$ ；其中正确的是．（填序号即可）

查看试题解析
16. 如图，在平面直角坐标系 $x O y$ 中，抛物线 $y = x^{2} - 1$ 与x轴交于A，B两点（点A在点B左侧），直线 $y = k x + b$ 经过点A；当 $b = 1$ 时，直线 $y = k x + b$ 分别与y轴，抛物线 $y = x^{2} - 1$ 交于 $P_{1}$ ， $Q_{1}$ 两点；当 $b = 2$ 时，直线 $y = k x + b$ 分别与y轴，抛物线 $y = x^{2} - 1$ 交于 $P_{2}$ ， $Q_{2}$ 两点；……；当 $b = n$ （ $n$ 为正整数）时，直线 $y = k x + b$ 分别与y轴，抛物线 $y = x^{2} - 1$ 交于 $P_{n}$ ， $Q_{n}$ 两点，则线段 $P_{n} Q_{n}$ 长为．（用含n的代数式表示）

查看试题解析

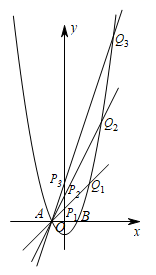
三、解答题

17. 用适当的方法解方程

(1)、 $x^{2} - 5 x - 6 = 0$ ；

(2)、 $2 x^{2} - 2 \sqrt{2} x + 1 = 0$ ．

查看试题解析
18. 如图，将 $△ A B C$ 绕点A逆时针旋转30°得到 $△ A B C$ ，且 $B$ ， $C$ 两点分别与B，C两点对应，延长 $B C$ 与 $B^{^{'}} C^{^{'}}$ 边交于点E，求 $∠ C E C$ 的度数．

查看试题解析
19. 如图，在一块长 $60 m$ 、宽 $30 m$ 的矩形地面内，修筑一横两竖三条道路，横、竖道路的宽度相同，余下的地面铺草坪，要使草坪面积达到 $1568 m^{2}$ ，求道路的宽．

查看试题解析
20. 按要求完成下列问题：

(1)、在平面直角坐标系中，描出二次函数 $y_{1} = - x^{2} + 2 x + 3$ 图象的顶点，图象与x轴，y轴交点，并画出二次函数 $y_{1} = - x^{2} + 2 x + 3$ 的图象（不必列表）；

(2)、已知一次函数 $y_{2} = k x + b$ ，当 $y_{1} > y_{2}$ 时，自变量x的取值范围为 $- 1 < x < 2$ ，请直接写出一次函数 $y_{2} = k x + b$ 的表达式．

查看试题解析
21. 如图，在 $△ A B C$ 中，点D为 $B C$ 边上一点，连接 $A D$ ，点H为 $A D$ 中点，延长 $B H$ 交 $A C$ 边于点E，求证： $\frac{A E}{C E} = \frac{B D}{B C}$ ．

查看试题解析
22. 如图，正比例函数 $y = k x$ 图象与反比例函数 $y = \frac{n}{x}$ 图象交于 $A (m ， - 1)$ ， $B (2 ， 1)$ 两点：

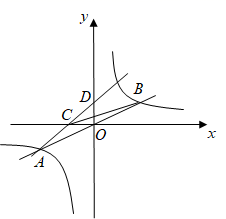(1)、求反比例函数 $y = \frac{n}{x}$ 的函数表达式；

(2)、点C为x轴负半轴上一点，直线 $A C$ 与y轴交于点D，且 $O C = O D$ ，求 $△ A C B$ 的面积．

查看试题解析
23. 如图，在平行四边形 $A B C D$ 中，点O为 $A D$ 边上一点，以O为圆心， $O A$ 为半径作 $⊙ O$ 恰好经过点B，与 $A D$ 边交于点E， $C D$ 边所在直线与 $⊙ O$ 相切，切点为H，连接 $A H$ ， $E H$ ，若 $2 ∠ H A B + ∠ C = 180 °$ ：

(1)、求证： $C B$ 为 $⊙ O$ 切线；

(2)、若 $D E = 1$ ，求 $⊙ O$ 半径．

查看试题解析
24. 某经销商以140元/件的价格购进一款服装，若以300元/件的价格出售，每周可售出300件，该经销商在“元旦”之前购进若干该款服装准备在“元旦”黄金周进行降价促销，若销售单价每降低1元，则每周可多售出5件，且“元旦”黄金周的销售量不超过500件：设“元旦”黄金周该款服装售价为x元/件，销售利润为y元：

(1)、求y与x之间的函数关系式；

(2)、当售价为多少元/件时，“元旦”黄金周的销售利润最大，最大利润为多少元？

查看试题解析
25.

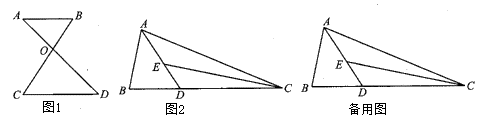(1)、基本模型：如图1， $A D$ 与 $B C$ 交于点O，且 $A B ∥ C D$ ，求证： $△ A O B ∽ △ D O C$ ；

(2)、模型应用：如图2，在 $△ A B C$ 中，点D为 $B C$ 边上一点，连接 $A D$ ，点E为线段 $A D$ 上一点，连接 $C E$ ，若 $\frac{A B}{C E} = \frac{1}{2}$ ， $∠ B A D = ∠ C E D$ ，求 $\frac{B D}{C D}$ 的值．

(3)、综合应用：在（2）的条件下，若 $A C = B C$ ， $C E$ 平分 $∠ B C A$ ， $∠ B A D = 45 °$ ， $A C = \sqrt{13}$ ，求 $A D$ 的长．

查看试题解析
26. 如图，在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} - 2 a x - 3 a (a \neq 0)$ 交x轴于A，B两点（点A在点B左侧），交y轴的正半轴于点C，

(1)、若 $O C = 3 O A$ ；
①求抛物线的解析式；
②点P为y轴上一动点，连接 $P B$ ，将线段 $P B$ 绕点P顺时针旋转90°得到线段 $P B$ ，若 $B$ 恰好落在抛物线 $y = a x^{2} - 2 a x - 3 a$ 上，求P点坐标；

(2)、点Q为抛物线上一动点，其横坐标为n，直线 $B Q$ 交y轴于点E，连接 $Q C$ ，当 $S_{△ Q C E} = S_{△ B O E}$ 时，请直接写出n的值．

查看试题解析