吉林省长春市德惠市2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $\sqrt{a}$ 是二次根式，则a的值可能是（　　）

A、﹣3 B、﹣2 C、﹣1 D、0

查看试题解析
2. 一元二次方程2x²﹣3x﹣4＝0的根的情况是（　　）

A、有一个实数根 B、有两个不相等的实数根 C、没有实数根 D、有两个相等的实数根

查看试题解析
3. 若 $\frac{a}{b} = \frac{3}{2}$ ，则 $\frac{a}{a - b}$ 等于（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{3}{2} .$ D、3.

查看试题解析
4. 将抛物线y＝（x﹣5）²+6向下平移2个单位，得到的新抛物线的顶点坐标是（　　）

A、（5，4） B、（6，5） C、（5，6） D、（5，8）

查看试题解析
5. 下列说法错误的是（　　）

A、不可能事件发生的概率是0 B、概率很小的事件不可能发生 C、必然事件发生的概率是1 D、随机事件发生的概率介于0和1之间

查看试题解析
6. 如图，直线l₁∥l₂ ，直线AB、CD相交于点E，若AE＝4，BE＝8，CD＝9，则线段CE的长为（　　）

A、3 B、5 C、7 D、9

查看试题解析
7. 如图，在△ABC中，∠C＝90°，设∠A，∠B，∠C所对的边分别为a，b，c，则（）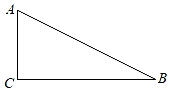

A、sinA＝ $\frac{a}{b}$ B、a＝sinB×c C、cosA＝ $\frac{b}{c}$ D、tanA＝ $\frac{b}{a}$

查看试题解析
8. 在平面直角坐标系中，二次函数y＝ax²+bx+c（a≠0）的图象如图所示，则下列结论正确的（　　）

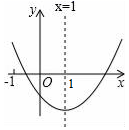A、ac＞0 B、b²﹣4ac＜0 C、4a+2b+c＜0 D、b＝2a

查看试题解析

二、填空题

9. 若最简二次根式 $\sqrt{2023 - m}$ 与 $\sqrt{2}$ 是同类二次根式，则m＝．

查看试题解析
10. 解一元二次方程x²﹣7x＝0的最佳方法是．

查看试题解析
11. 在一个不透明的袋子中，装有若干个除颜色外都相同的小球，其中有8个红球和n个黑球，从袋中任意摸出一个球，若摸出黑球的概率是 $\frac{3}{5}$ ，则n＝．

查看试题解析
12. 如图，某同学利用标杆BE测量教学楼的高度，已知标杆BE高1.5m，测得AB＝1.2m，BC＝12.8m，则教学楼CD的高度是 m．

查看试题解析
13. 如图，在平面直角坐标系中，等边△ABC与等边△BDE是以原点为位似中心的位似图形，且相似比为 $\frac{1}{3}$ ，点A、B、D在x轴上，若等边△BDE的边长为6，则点C的坐标为．

查看试题解析
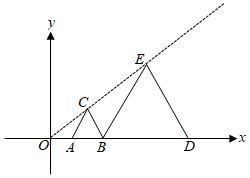14. 如图，在平面直角坐标系中，抛物线y=﹣ $\frac{1}{2}$ （x﹣3）²+m与y= $\frac{2}{3}$ （x+2）²+n的一个交点为A．已知点A的横坐标为1，过点A作x轴的平行线，分别交两条抛物线于点B、C（点B在点A左侧，点C在点A右侧），则 $\frac{A B}{A C}$ 的值为．

查看试题解析

三、解答题

15. 计算： $\sqrt{18} \div \sqrt{\frac{2}{3}}$ •tan60°．

查看试题解析
16. 新高考“3+1+2”是指：3，语数外三科是必考科目；1，物理、历史两科中任选一科；2，化学、生物、地理、政治四科中任选两科．某同学确定选择“物理”，但他不确定其它两科选什么，于是他做了一个游戏：他拿来四张不透明的卡片，正面分别写着“化学、生物、地理、政治”，再将这四张卡片背面朝上并打乱顺序，然后从这四张卡片中随机抽取两张，请你用画树状图（或列表）的方法，求该同学抽出的两张卡片是“化学、政治”的概率．

查看试题解析
17. 如图，在 $△ A B C$ 中， $B C = 6$ ，D为AC延长线上一点， $A C = 3 C D$ ， $∠ C B D = ∠ A$ ，过点D作DE//AB交BC的延长线于点E．

(1)、求证： $△ E C D ∽ △ E D B$ ；

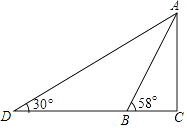
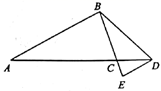(2)、求DE的长度．

查看试题解析
18. 如图，某游乐园有一个滑梯高度AB，高度AC为3米，倾斜角度为58°．为了改善滑梯AB的安全性能，把倾斜角由58°减至30°，调整后的滑梯AD比原滑梯AB增加多少米？（精确到0.1米）
（参考数据：sin58°=0.85，cos58°=0.53，tan58°=1.60）

查看试题解析
19. 图①、图②、图③均是 $5 \times 4$ 的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1，点A、B、C、D均在格点上在图②、图③中，只用无刻度的直尺，在给定的正方形网格中，按要求画图，保留作图痕迹，不要求写出画法．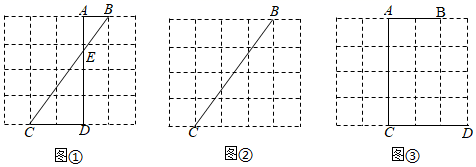

(1)、如图①， $\frac{B E}{C E} =$ ．

(2)、如图②，在 $B C$ 上找一点F，使 $B F = 2$ ．

(3)、如图③，在 $A C$ 上找一点M，连结 $B M$ 、 $D M$ ，使 $△ A B M ∽ △ C D M$ ．

查看试题解析
20. “疫情”期间，某商场积压了一批商品，现欲尽快清仓．老板决定在抖音直播间降价促销，据调查发现，若每件商品盈利50元，可售出500件，商品单价每下降1元，可多售出20件，设每件商品降价x元．

(1)、每件商品降价x元后，可售出商品件（用含x的代数式表示）；

(2)、若要使销售该商品的总利润达到28000元，并能尽快清仓，则每件商品应降价多少元？

查看试题解析
21.

(1)、（教材呈现）下面是华东师大版九年级上册数学教材第78页的部分内容．

例2如图，在△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于点G，求证： $\frac{G E}{C E} = \frac{G D}{A D} = \frac{1}{3}$ ．

证明：连结ED．

请根据教材提示，结合图①，写出完整的证明过程．

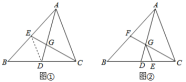(2)、（结论应用）如图②，在△ABC中，D、F分别是边BC、AB的中点，AD、CF相交于点G，GE∥AC交BC于点E，则DE：BC＝．

查看试题解析
22. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90^{°}$ ， $A B = 3$ ， $B C = 4$ ，动点P从点A出发，沿AC方向以每秒1个单位长度的速度向终点C运动，将线段AP绕点P逆时针旋转90°，得到线段PQ，过点Q作 $Q M ⊥ A B$ ，交射线AC于点M．设点P的运动时间为t秒．

(1)、线段MP的长为（用含t的代数式表示）．

(2)、当点M与点C重合时，求t的值．

(3)、设 $△ P Q M$ 与 $△ A B C$ 重叠部分图形的面积为S（ $S > 0$ ），求S与t之间的函数关系式．

(4)、取线段PM的中点H，作直线BH，当直线BH将 $△ P Q M$ 分成的两部分图形的面积比为1：3时，直接写出此时t的值．

查看试题解析
23. 已知二次函数y＝x²﹣2mx+2m²﹣1（m为常数）．

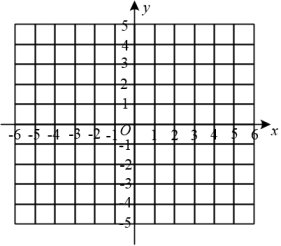(1)、当m＝1时，求该二次函数的解析式，并将其化为顶点式．

(2)、将该函数图象沿过其顶点且平行于x轴的直线翻折，得到新函数图象．
①求新函数的表达式，并说明新函数图象始终经过一个定点．
②已知点A（﹣2，﹣1）、B（2，﹣1），若新函数图象与线段AB只有一个公共点，直接写出m的取值范围．

查看试题解析