吉林省长春市朝阳区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列关于x的函数中，一定是二次函数的是（）

A、 $y = - 3 x$ B、 $x y = 2$ C、 $y = a x^{2} + b x + c$ D、 $y = 2 x^{2} + 5$

查看试题解析
2. 一元二次方程 $x^{2} + 2 x + 3 = 0$ 的根的情况是（）

A、有两个相等的实数根 B、只有一个实数根 C、有两个不相等的实数根 D、没有实数根

查看试题解析
3. 将抛物线 $y = 3 x^{2}$ 先向左平移2个单位，再向上平移6个单位，所得抛物线对应的函数表达式为（）

A、 $y = 3 {(x - 2)}^{2} + 6$ B、 $y = 3 {(x - 2)}^{2} - 6$ C、 $y = 3 {(x + 2)}^{2} + 6$ D、 $y = 3 {(x + 2)}^{2} - 6$

查看试题解析
4. 如图，直线a//b//c，直线 $l_{1}$ 、 $l_{2}$ 与这三条平行线分别交于点A、B、C和点D、E、F．若 $A B ： B C = 1 ： 2$ ， $D E = 3$ ，则EF的长为（）

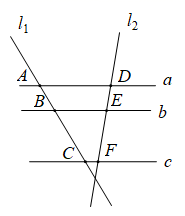A、1.5 B、6 C、9 D、12

查看试题解析
5. 如图，在 $A$ 岛周围20海里水域有暗礁，一艘轮船由西向东航行到 $O$ 处时，发现岛在北偏东64°的方向且与轮船相距52海里．若该轮船不改变航向，为航行安全，需要计算 $A$ 到 $O B$ 的距离 $A C$ ．下列算法正确的是（）

A、 $A C = 52 \cos 64 °$ B、 $A C = \frac{52}{\cos 64 °}$ C、 $A C = 52 \sin 64 °$ D、 $A C = 52 \tan 64 °$

查看试题解析
6. 对于抛物线 $y = - {(x + 1)}^{2} + 3$ ，下列说法中正确的是（）

A、开口向上 B、对称轴是直线 $x = 1$ C、当 $x > - 1$ 时，y随x的增大而增大 D、函数的最大值是3

查看试题解析
7. 若抛物线 $y = a x^{2}$ 经过点 $P (- \sqrt{7} ， 4)$ ，则该抛物线一定还经过点（）

A、 $(4 ， - \sqrt{7})$ B、 $(\sqrt{7} ， 4)$ C、 $(- 4 ， \sqrt{7})$ D、 $(- \sqrt{7} ， - 4)$

查看试题解析
8. 将抛物线 $y = x^{2} - 4 x - 2$ 在x轴上方的部分记为 $M_{1}$ ，在x轴上及其下方的部分记为 $M_{2}$ ，将 $M_{1}$ 沿x轴向下翻折得到 $M_{3}$ ， $M_{2}$ 和 $M_{3}$ 两部分组成的图象记为M．若直线 $y = m$ 与M恰有2个交点，则m的取值范围为（）

A、 $m > 6$ 或 $m < - 6$ B、 $m = 0$ 或 $m < - 6$ C、 $- 6 < m < 6$ D、 $m = 0$ 或 $m > 6$

查看试题解析

二、填空题

9. 计算： $\frac{1}{2} s i n 60 ° =$ ．

查看试题解析
10. 转动如图所示的这些可以自由转动的转盘（转盘均被等分），当转盘停止转动后，根据“指针落在白色区域内”的可能性的大小，将转盘的序号按事件发生的可能性从小到大排列为．

查看试题解析
11. 如图， $△$ ABC中，D是BC中点，AE平分∠BAC，AE⊥BE，AB=3，AC=5，则DE= ．

查看试题解析
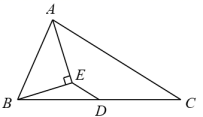12. 如图，在平面直角坐标系中，若直线 $y = m x + n$ 与抛物线 $y = a x^{2} + b x + c$ 分别交于 $A (- 1 ， p)$ 、 $B (2 ， q)$ ，则关于x的不等式 $m x + n < a x^{2} + b x + c$ 的解集是．

查看试题解析
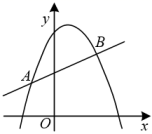13. 若关于x的一元二次方程 $2 x^{2} + 3 x - 5 = 0$ 的一个根是m，则 $4 m^{2} + 6 m - 2021$ 的值为．

查看试题解析
14. 一名运动员在平地上推铅球，铅球出手时离地面的高度为 $\frac{9}{5}$ 米，出手后铅球离地面的高度y（米）与水平距离x（米）之间的函数关系式为 $y = - \frac{3}{40} x^{2} + b x + c$ ，当铅球离地面的高度最大时，与出手点水平距离为5米，则该运动员推铅球的成绩为米．

查看试题解析

三、解答题

15. $\sqrt{27} - \sqrt{12} + \sqrt{45}$

查看试题解析
16. 解方程： $x^{2} + 5 x - 2 = 0$ ．

查看试题解析
17. 图①、图②、图③均是 $4 \times 4$ 的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A、B、C均在格点上．只用无刻度的直尺，在给定的网格中，按照要求作图（保留作图痕迹）．

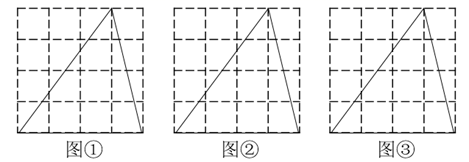(1)、在图①中作 $△ A B C$ 的中线BD．

(2)、在图②中作 $△ A B C$ 的高BE．

(3)、在图③中作 $△ A B C$ 的角平分线BF．

查看试题解析
18. 2021年是中国辛丑牛年，小明将收集到的以下3张牛年邮票分别放到A、B、C三个完全相同的不透明盒子中，现从中随机抽取一个盒子．

(1)、“小明抽到面值为80分的邮票”是事件（填“随机”“不可能”或“必然”）；

(2)、小明先随机抽取一个盒子记下邮票面值后将盒子放回，再随机抽取一个盒子记下邮票面值，用画树状图（或列表）的方法，求小明抽到的两个盒子里邮票的面值恰好相等的概率．

查看试题解析
19. 若抛物线 $y = - x^{2} + b x + c$ 经过 $(- 1 ， 0)$ 和 $(5 ， 0)$ ．

(1)、求抛物线对应的二次函数表达式；

(2)、当 $0 < x < 5$ 时，直接写出y的取值范围是．

查看试题解析
20. 如图，在平行四边形ABCD中， $A D = 3$ ，过点B作 $B E ⊥ C D$ 于E，连结AE， $∠ A E B = 60 °$ ， F为AE上一点，且 $∠ B F E = ∠ C$ ．

(1)、求证： $△ A B F ∽ △ E A D$ ．

(2)、BF的长为．

查看试题解析
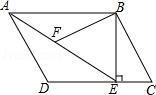21. 如图，某矩形花园ABCD一边靠墙，墙长35m，另外三边用长为69m的篱笆围成，其中一边开有一扇宽为1m的门（不包括篱笆）．设矩形花园ABCD垂直于墙的一边AB长为xm，面积为 $S m^{2}$ ．

(1)、BC的长为m（用含x的代数式表示）．

(2)、求S与x之间的函数关系式，并写出x的取值范围．

(3)、求花园面积S的最大值．

查看试题解析
22.

(1)、（教材呈现）下面内容是华师版八下第75页练习2
如图①，如果直线 $l_{1}$ // $l_{2}$ ，那么 $△ A B C$ 的面积和 $△ D B C$ 的面积是相等的．
请你对上述的结论加以证明．

(2)、（方法操究）如图②，在 $△ A B C$ 中，点D、E分别在边AB、AC上， $D E$ // $B C$ ， $\frac{A D}{A B} = \frac{1}{3}$ ，点F在边BC上，连结DF、EF．求证： $S_{△ D E F} = \frac{2}{9} S_{△ A B C}$ ．

(3)、（拓展应用）如图③，在 $△ A B C$ 中，D、E分别在边AB、AC上． $\frac{A D}{D B} = \frac{A E}{E C} = \frac{3}{4}$ ，在线段DE上取一点F（点F不与点D、E重合），连结AF并延长交BC于点G．点M、N在线段BC上，且 $B M = 2 E F$ ， $C N = 2 D F$ ．若 $S_{△ A B C} = 49$ ，则 $S_{△ B F M} + S_{△ C E N} =$ ．

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A B = 5$ ， $A C = 4$ ．动点P从点A出发，沿AB以每秒4个单位长度的速度向终点B运动．过点P作 $P Q ⊥ A B$ 交AC或BC于点Q，分别过点P、Q作AC、AB的平行线交于点M．设 $△ P Q M$ 与 $△ A B C$ 重叠部分的面积为S，点P运动的时间为 $t (t > 0)$ 秒．

(1)、当点Q在AC上时，CQ的长为（用含t的代数式表示）．

(2)、当点M落在BC上时，求t的值．

(3)、当 $△ P Q M$ 与 $△ A B C$ 的重合部分为三角形时，求S与t之间的函数关系式．

(4)、点N为PM中点，直接写出点N到 $△ A B C$ 的两个顶点的距离相等时t的值．

查看试题解析
24. 在平面直角坐标系中，抛物线 $L ： y = \frac{1}{2} x^{2} - m x + 2 m + 3$ （m是常数）的顶点为A．

(1)、用含m的代数式表示抛物线L的对称轴．

(2)、当 $2 \leq x \leq 3$ ，抛物线L的最高点的纵坐标为6时，求抛物线L对应的函数表达式．

(3)、已知点 $B (- 3 ， 2)$ 、 $C (2 ， 7)$ ，当 $- 3 < m < 2$ 时，设 $△ A B C$ 的面积为S．求S与m之间的函数关系式，并求S的最小值．

(4)、已知矩形MNPQ的四个顶点的坐标分别为 $M (3 ， 3 - m)$ 、 $N (3 ， 3 + \frac{1}{2} m)$ 、 $P (5 + m ， 3 + \frac{1}{2} m)$ 、 $Q (5 + m ， 3 - m)$ ，当抛物线L与边MN、PQ各有1个交点分别为点D、E时，若点D到y轴的距离和点E到x轴的距离相等，直接写出m的值．

查看试题解析