黑龙江省齐齐哈尔市铁锋区2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 垃圾分类一小步,低碳生活一大步,垃圾桶上常有以下四种垃圾分类标识的图案和文字说明其中图案是中心对称图形的是( )A、
 有害垃圾
B、
有害垃圾
B、 厨余垃圾
C、
厨余垃圾
C、 其它垃圾
D、
其它垃圾
D、 可回收物
2. 下列方程中是关于x的一元二次方程的是( )A、 B、ax2+bx+c=0 C、(x﹣1)(x﹣2)=0 D、3x2+2=x2+2(x﹣1)23. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为( )
可回收物
2. 下列方程中是关于x的一元二次方程的是( )A、 B、ax2+bx+c=0 C、(x﹣1)(x﹣2)=0 D、3x2+2=x2+2(x﹣1)23. 如图,线段AB两个端点的坐标分别为A(6,6),B(8,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的 后得到线段CD,则端点C的坐标为( )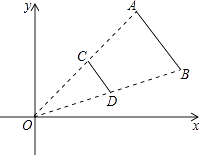 A、(3,3) B、(4,3) C、(3,1) D、(4,1)4. 下列事件中,为必然事件的是( )A、明天要下雨 B、太阳从东边升起 C、﹣2>﹣1 D、打开电视机,它正在播广告5. 如图,在中, , , D,E分别在、上,将沿折叠,使点A落在点处,若为的中点,则折痕的长为( )
A、(3,3) B、(4,3) C、(3,1) D、(4,1)4. 下列事件中,为必然事件的是( )A、明天要下雨 B、太阳从东边升起 C、﹣2>﹣1 D、打开电视机,它正在播广告5. 如图,在中, , , D,E分别在、上,将沿折叠,使点A落在点处,若为的中点,则折痕的长为( )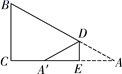 A、 B、2 C、3 D、46. 一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20,则y与x的函数图象大致是( )A、
A、 B、2 C、3 D、46. 一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20,则y与x的函数图象大致是( )A、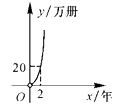 B、
B、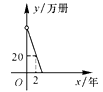 C、
C、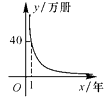 D、
D、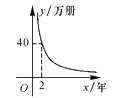 7. 将抛物线的图象向上平移2个单位后得到的图象,那么原图象的表达式是( )A、 B、 C、 D、8. 如图,小芳和爸爸正在散步,爸爸身高1.8m,他在地面上的影长为2.1m.若小芳身高只有1.2m,则她的影长为( )
7. 将抛物线的图象向上平移2个单位后得到的图象,那么原图象的表达式是( )A、 B、 C、 D、8. 如图,小芳和爸爸正在散步,爸爸身高1.8m,他在地面上的影长为2.1m.若小芳身高只有1.2m,则她的影长为( )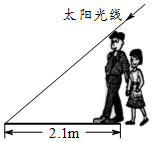 A、1.2m B、1.4m C、1.6m D、1.8m9. 已知点是反比例函数的图象上的两点,若 , 则下列结论正确的是( )A、 B、 C、 D、10. 如图,二次函数 图象的一部分与x轴的一个交点坐标为 ,对称轴为 ,结合图象给出下列结论:
A、1.2m B、1.4m C、1.6m D、1.8m9. 已知点是反比例函数的图象上的两点,若 , 则下列结论正确的是( )A、 B、 C、 D、10. 如图,二次函数 图象的一部分与x轴的一个交点坐标为 ,对称轴为 ,结合图象给出下列结论:
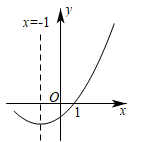
① ;
② ;
③关于x的一元二次方程 的两根分别为-3和1;
④若点 , , 均在二次函数图象上,则 ;
⑤ (m为任意实数).
其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若一元二次方程的二次项系数为1,常数项为0,它的一个根为2,则该方程为。12. 一个圆锥的侧面展开图是半圆,则圆锥母线长与底面半径的比为 .13. 某校图书馆利用节假日面向社会开放.据统计,第一个月进馆500人次,进馆人次逐月增加,第三个月进馆720人次,设该图书馆第二个月、第三个月进馆人次的平均增长率为x,则可列方程为 .14. 如图,已知 是 的直径, 是 的切线,连接 交 于点D,连接 .若 ,则 的度数是 .
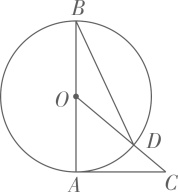 15. 如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的的圆心P在射线OA上,且与点O的距离为6cm,以1cm/s的速度沿由A向B的方向移动,那么与直线CD相切时,圆心P的运动时间为 .
15. 如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的的圆心P在射线OA上,且与点O的距离为6cm,以1cm/s的速度沿由A向B的方向移动,那么与直线CD相切时,圆心P的运动时间为 .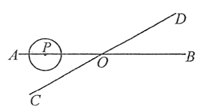 16. 如图,在矩形中,点N为边上不与B、C重合的一个动点,过点N作交于点M,交于点E,以为对称轴折叠矩形 , 点A、B的对应点分别是G、F,连接、 , 若 , , 当为直角三角形时,的长为 .
16. 如图,在矩形中,点N为边上不与B、C重合的一个动点,过点N作交于点M,交于点E,以为对称轴折叠矩形 , 点A、B的对应点分别是G、F,连接、 , 若 , , 当为直角三角形时,的长为 . 17. 如图,边长为1的正六边形放置于平面直角坐标系中,边在x轴正半轴上,顶点F在y轴正半轴上,将正六边形绕坐标原点O顺时针旋转,每次旋转 , 那么经过第2022次旋转后,顶点D的坐标为 .
17. 如图,边长为1的正六边形放置于平面直角坐标系中,边在x轴正半轴上,顶点F在y轴正半轴上,将正六边形绕坐标原点O顺时针旋转,每次旋转 , 那么经过第2022次旋转后,顶点D的坐标为 .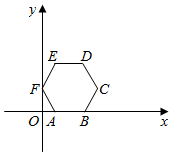
三、解答题
-
18. 解方程:(1)、(2)、19. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好.
 (1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)20. 已知关于x的一元二次方程有两个不等的实根.(1)、求a的取值范围;(2)、当a取最大整数值时,的三条边长均满足关于x的一元二次方程 , 求的周长.21. 如图, 为 的直径,射线 交 于点F,点C为劣弧 的中点,过点C作 ,垂足为E,连接 .
(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)20. 已知关于x的一元二次方程有两个不等的实根.(1)、求a的取值范围;(2)、当a取最大整数值时,的三条边长均满足关于x的一元二次方程 , 求的周长.21. 如图, 为 的直径,射线 交 于点F,点C为劣弧 的中点,过点C作 ,垂足为E,连接 .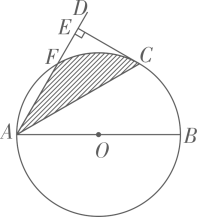 (1)、求证: 是 的切线;(2)、若 ,求阴影部分的面积.22. 某气象研究中心观测到一场沙尘暴从发生到减弱的全过程.开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速 (千米/小时)与时间 (小时)成反比例函数关系缓慢减弱.
(1)、求证: 是 的切线;(2)、若 ,求阴影部分的面积.22. 某气象研究中心观测到一场沙尘暴从发生到减弱的全过程.开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速 (千米/小时)与时间 (小时)成反比例函数关系缓慢减弱. (1)、这场沙尘暴的最高风速是千米/小时,最高风速维持了小时;(2)、当 时,求出风速 (千米/小时)与时间 (小时)的函数关系式;(3)、在这次沙尘暴形成的过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻为“危险时刻”,那么在沙尘暴整个过程中,求“危险时刻”共有几小时.23. 综合与实践
(1)、这场沙尘暴的最高风速是千米/小时,最高风速维持了小时;(2)、当 时,求出风速 (千米/小时)与时间 (小时)的函数关系式;(3)、在这次沙尘暴形成的过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻为“危险时刻”,那么在沙尘暴整个过程中,求“危险时刻”共有几小时.23. 综合与实践如图1,已知点G在正方形ABCD的对角线AC 上,GE⊥BC,垂足为E,GF⊥CD,垂足为F.

 (1)、(证明与推断)
(1)、(证明与推断)①四边形CEGF的形状是;
②的值为;
(2)、(探究与证明)在图1的基础上,将正方形CEGF绕点C按顺时针方向旋转α角(0°<α><45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;
(3)、(拓展与运用)如图3,在(2)的条件下,正方形CEGF 在旋转过程中,当B、E、F三点共线时,探究AG和GE的位置关系,并说明理由.
24. 综合与探究如图,在平面直角坐标系中,抛物线与x轴交于点A、B,与y轴交于点C,连接 , , 对称轴为 , 点D为此抛物线的顶点.
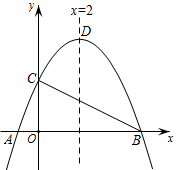
 (1)、求抛物线的解析式;(2)、抛物线上C,D两点之间的距离是;(3)、点E是第一象限内抛物线上的动点,连接和 . 求面积的最大值;(4)、点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点P的坐标.
(1)、求抛物线的解析式;(2)、抛物线上C,D两点之间的距离是;(3)、点E是第一象限内抛物线上的动点,连接和 . 求面积的最大值;(4)、点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点P的坐标.