黑龙江省齐齐哈尔市梅里斯达斡尔族区2021-2022学年九年级上学期期末考试数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 下列是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 将一个等腰三角形绕它的底边旋转一周得到的几何体为( )A、
2. 将一个等腰三角形绕它的底边旋转一周得到的几何体为( )A、 B、
B、 C、
C、 D、
D、 3. 下列一元二次方程中没有实数根的方程是( )A、(x﹣1)2=1 B、x2+2x﹣10=0 C、x2+4=7 D、x2+x+1=04.
3. 下列一元二次方程中没有实数根的方程是( )A、(x﹣1)2=1 B、x2+2x﹣10=0 C、x2+4=7 D、x2+x+1=04.如图所示,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,则∠BOF为( )
 A、35° B、30° C、25° D、20°5. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD的度数为( )
A、35° B、30° C、25° D、20°5. 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD的度数为( )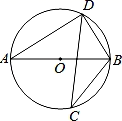 A、32° B、58° C、64° D、116°6. 有三张正面分别写有数字﹣2,1,3的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后把这张放回去,再从三张卡片中随机抽一张,以其正面的数字作为b的值,则点(a,b)在第一象限的概率为( )A、 B、 C、 D、7. 在同一平面直角坐标系中,函数 和函数 (m是常数,且 )的图象可能是( ).A、
A、32° B、58° C、64° D、116°6. 有三张正面分别写有数字﹣2,1,3的卡片,它们背面完全相同,现将这三张卡片背面朝上洗匀后随机抽取一张,以其正面数字作为a的值,然后把这张放回去,再从三张卡片中随机抽一张,以其正面的数字作为b的值,则点(a,b)在第一象限的概率为( )A、 B、 C、 D、7. 在同一平面直角坐标系中,函数 和函数 (m是常数,且 )的图象可能是( ).A、 B、
B、 C、
C、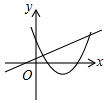 D、
D、 8. 下列说法正确的是( )A、三点确定一个圆 B、同圆中,圆周角等于圆心角的一半 C、平分弦的直径垂直于弦 D、一个三角形只有一个外接圆9. 某水果园2017年水果产量为50吨,2019年水果产量为70吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为 ,则根据题意可列方程为( )A、 B、 C、 D、10. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>﹣3b;(3)7a﹣3b+2c>0;(4)若点A(﹣3,y1)、点B(﹣ ,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( )
8. 下列说法正确的是( )A、三点确定一个圆 B、同圆中,圆周角等于圆心角的一半 C、平分弦的直径垂直于弦 D、一个三角形只有一个外接圆9. 某水果园2017年水果产量为50吨,2019年水果产量为70吨,求该果园水果产量的年平均增长率.设该果园水果产量的年平均增长率为 ,则根据题意可列方程为( )A、 B、 C、 D、10. 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>﹣3b;(3)7a﹣3b+2c>0;(4)若点A(﹣3,y1)、点B(﹣ ,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 . 其中正确的结论有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 我国是全球抗疫最成功的国家,免费打疫苗人数已经超过10亿人,但我们依然要严格遵守防疫四宝,保护自己也保护他人.到目前为止,全球新冠病毒确诊病例已经接近270000000人,死亡人数已经超过5300000人,特别是变异毒株奥密克戎的出现,让全人类抗疫面临更大挑战.全球新冠病毒确诊病例270000000人用科学记数法表示为:人.12. 一个用电器的电阻是可调节的,其调节范围为:110~220Ω.已知电压为220ᴠ,这个用电器的功率P的范围是: w.(P表示功率,R表示电阻,U表示电压,三者关系式为:P·R=U²)13. 如图,□ 中, , , 的周长为25,则 的周长为 .
 14. 三角形两边长分别是4和2,第三边长是2x2﹣9x+4=0的一个根,则三角形的周长是 .15. 如图,双曲线 经过 斜边 的中点 ,与直角边 交于点 .过点 作 于点 ,连接 ,则 的面积是 .
14. 三角形两边长分别是4和2,第三边长是2x2﹣9x+4=0的一个根,则三角形的周长是 .15. 如图,双曲线 经过 斜边 的中点 ,与直角边 交于点 .过点 作 于点 ,连接 ,则 的面积是 .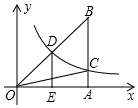 16. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′,若AB=4,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 . (结果保留π).
16. 如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′,若AB=4,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是 . (结果保留π).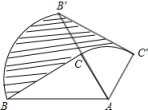 17. 一块材料形状是Rt△ABC,∠C=90°量得边AC=6cm,AB =10cm,用它来加工一个正方形零件,使正方形的至少一边在Rt△ABC的边上,其余顶点在其它边上,则这个正方形零件的边长为: .
17. 一块材料形状是Rt△ABC,∠C=90°量得边AC=6cm,AB =10cm,用它来加工一个正方形零件,使正方形的至少一边在Rt△ABC的边上,其余顶点在其它边上,则这个正方形零件的边长为: .
三、解答题
-
18. 用适当的方法解下列方程.(1)、3x(x+3)=2(x+3)(2)、2x2﹣4x﹣3=0.19. 如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于A、B两点,其中点A的坐标为(﹣1,4),点B的坐标为(4,n).
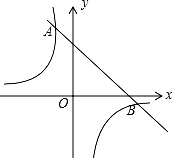 (1)、求这两个函数的表达式;(2)、根据图象,直接写出满足k1x+b>的x的取值范围.20. 如图,在每个小正方形的边长均为1的方格纸中,线段 的端点 、 均在小正方形的顶点上.
(1)、求这两个函数的表达式;(2)、根据图象,直接写出满足k1x+b>的x的取值范围.20. 如图,在每个小正方形的边长均为1的方格纸中,线段 的端点 、 均在小正方形的顶点上.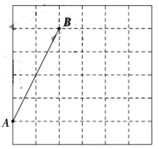 (1)、在方格纸中画出以 为一条直角边的等腰直角 ,顶点 在小正方形的顶点上.(2)、在方格纸中画出 的中线 ,将线段 绕点 顺时针旋转 得到线段 ,画出旋转后的线段 ,连接 ,直接写出四边形 的面积.21. 如图,以△ABC的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,∠D=30°.
(1)、在方格纸中画出以 为一条直角边的等腰直角 ,顶点 在小正方形的顶点上.(2)、在方格纸中画出 的中线 ,将线段 绕点 顺时针旋转 得到线段 ,画出旋转后的线段 ,连接 ,直接写出四边形 的面积.21. 如图,以△ABC的边BC为直径作⊙O,点A在⊙O上,点D在线段BC的延长线上,AD=AB,∠D=30°. (1)、求证:直线AD是⊙O的切线;(2)、过点O作OE∥AB交AC与点E,若直径BC=4,求OE的长.22. 如图,已知正方形中,点E是边延长线上一点,连接 , 过点B作 , 垂足为点F,与交于点G.
(1)、求证:直线AD是⊙O的切线;(2)、过点O作OE∥AB交AC与点E,若直径BC=4,求OE的长.22. 如图,已知正方形中,点E是边延长线上一点,连接 , 过点B作 , 垂足为点F,与交于点G. (1)、求证:;(2)、若 , , 求 BG的长.23. 随着冬季的来临,为了方便冰雪爱好者雪上娱乐,某体育用品商店购进一批简易滑雪板,每件进价为100元,售价为130元,每星期可卖出80件,由于商品库存较多,商家决定降价促销,根据市场调查,每件降价1元,每星期可多卖出4件.(1)、设商家每件滑雪板降价x元,每星期的销售量为y件,写出y与x之间的函数关系式:(2)、降价后,商家要使每星期的利润最大,应将售价定为每件多少元?最大销售利润多少?24. 如图,在平面直角坐标系中,已知直线与x轴交于点A,与y轴交于点B,过A、B两点的抛物线与x轴交于另一点 .
(1)、求证:;(2)、若 , , 求 BG的长.23. 随着冬季的来临,为了方便冰雪爱好者雪上娱乐,某体育用品商店购进一批简易滑雪板,每件进价为100元,售价为130元,每星期可卖出80件,由于商品库存较多,商家决定降价促销,根据市场调查,每件降价1元,每星期可多卖出4件.(1)、设商家每件滑雪板降价x元,每星期的销售量为y件,写出y与x之间的函数关系式:(2)、降价后,商家要使每星期的利润最大,应将售价定为每件多少元?最大销售利润多少?24. 如图,在平面直角坐标系中,已知直线与x轴交于点A,与y轴交于点B,过A、B两点的抛物线与x轴交于另一点 .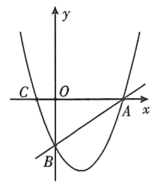 (1)、求抛物线的解析式和顶点坐标;(2)、探究1:在抛物线上直线AB下方是否存在一点P,使△ABP面积最大?若存在,请求出点P的坐标,若不存在,请说明理由;(3)、探究2:在(2)的基础上,平面内是否存在一点M使以A、B、P、M为顶点的四边形是平行四边形?若存在请直接写出M点坐标,若不存在请说明理由.
(1)、求抛物线的解析式和顶点坐标;(2)、探究1:在抛物线上直线AB下方是否存在一点P,使△ABP面积最大?若存在,请求出点P的坐标,若不存在,请说明理由;(3)、探究2:在(2)的基础上,平面内是否存在一点M使以A、B、P、M为顶点的四边形是平行四边形?若存在请直接写出M点坐标,若不存在请说明理由.