黑龙江省佳木斯市前进区2021-2022学年九年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、填空题

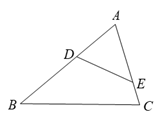
1. 到2020年底我国脱贫攻坚战取得全面胜利，现行标准下98990000农村贫困人口全部脱贫，将数据98990000科学记数法表示为．

查看试题解析
2. 函数 $y = \frac{2}{x - 4}$ 中，自变量x取值范围是．

查看试题解析
3. 如图，点 $D$ ， $E$ 分别在△ $A B C$ 的 $A B$ ， $A C$ 边上．只需添加一个条件即可证明△ $A D E$ ∽△ $A C B$ ，这个条件可以是．（写出一个即可）

查看试题解析
4. 小明和小亮在玩“石头、剪子、布”的游戏，两人一起做同样手势的概率是．

查看试题解析
5. 若不等式组 ${\begin{array}{l} 2 x - 4 > 0 \\ x < m \end{array}$ 无解，则m的取值范围是．

查看试题解析
6. 如图，点A、B、C是半径为4的⊙O上的三个点，若∠BAC＝45°，则弦BC的长等于．

查看试题解析
7. 一个圆锥的底面圆半径为6cm，圆锥侧面展开图扇形的圆心角为240°，则圆锥的母线长为 cm．

查看试题解析
8. 如图，AB是半圆O的直径，AB＝4，点C，D在半圆上，OC⊥AB， $\overset{⌢}{B D} = 2 \overset{⌢}{C D}$ ，点P是OC上的一个动点，则BP＋DP的最小值为．

查看试题解析
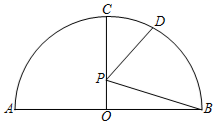9. 如图，矩形ABCD中，AD＝4，AB＝10，P为CD边上的动点，当DP＝时，△ADP与△BCP相似．

查看试题解析
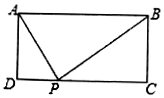10. 如图，在x轴的正半轴上依次截取OA₁＝A₁A₂＝A₂A₃ ， …，过点A₁、A₂、A₃、…分别作x轴的垂线与反比例函数y $＝ \frac{2}{x}$ （x≠0）的图象相交于点P₁、P₂、P₃、…，得直角三角形OP₁A₁、A₁P₂A₂、A₂P₃A₃、…，设其面积分别为S₁、S₂、S₃、…，则Sn的值为．

查看试题解析

二、单选题

11. 下列运算正确的是（）

A、2a＋3a＝6a B、 $(- 3 a)^{2} = 6 a^{2}$ C、 $(a - b)^{2} = a^{2} - b^{2}$ D、3 $\sqrt{2} \times \sqrt{2} ＝$ 6

查看试题解析
12. 下列标志是中心对称图形，但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
13. 八个大小相同的正方体搭成的几何体如图所示，其主视图是（）

A、 B、 C、 D、

查看试题解析
14. 在春季运动会中，有9名学生参加100米比赛，并且他们的最终成绩各不相同，若一名学生想知道自己能否进入前5名，除了要了解自己的成绩外，还要了解这9名学生成绩的（）

A、众数 B、中位数 C、平均数 D、方差

查看试题解析
15. 新型冠状病毒肺炎具有人传人性，调查发现1人感染病毒后如果不隔离，那么经过两轮传染将会有225人感染，若设1人平均感染x人，则x为（）

A、14 B、15 C、16 D、17

查看试题解析
16. 已知关于 $x$ 的分式方程 $\frac{m - 2}{x + 1} = 1$ 的解是非正数，则m的取值范围是（）

A、 $m \leq 3$ B、 $m \leq 3$ 且 $m \neq 2$ C、 $m < 3$ D、 $m < 3$ 且 $m \neq 2$

查看试题解析
17. 周末，小明的妈妈让他到药店购买口罩和消精湿巾，已知口罩每包3元，酒精湿巾每包2元，共用了30元钱（两种物品都买），小明的购买方案共有（）

A、3种 B、4种 C、5种 D、6种

查看试题解析
18. 如图，点P在反比例函数y= $\frac{k}{x}$ （k≠0）的图象上，PA⊥x轴于点A，△PAO的面积为2，则k的值为（　　）

A、1 B、2 C、4 D、6

查看试题解析
19. 如图，点P是▱ABCD边AD上的一点，E，F分别是BP，CP的中点，已知▱ABCD面积为16，那么△PEF的面积为（）

A、8 B、6 C、4 D、2

查看试题解析
20. 在锐角△ABC中，∠BAC＝60°，BN、CM为高，P为BC的中点，连接MN、MP、NP，则结论：①NP＝MP；②AN：AB＝AM：AC；③BN＝2AN；④当∠ABC＝60°时，MN∥BC，一定正确的有（）

A、①②③ B、②③④ C、①②④ D、①④

查看试题解析

三、解答题

21. 先化简，再求值： $(\frac{x + 1}{x - 2} - 1) \div \frac{x^{2} - 2 x}{x^{2} - 4 x + 4}$ ，其中x=tan60°．

查看试题解析
22. 如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（1，4），B（1，1），C（3，1）．
⑴画出△ABC关于x轴对称的△A₁B₁C₁；
⑵画出△ABC绕点O逆时针旋转90°后的△A₂B₂C₂；
⑶在（2）的条件下，求线段BC扫过的面积（结果保留π）．

查看试题解析
23. 如图，抛物线y＝ $- x^{2}$ ＋bx＋c经过坐标原点，并与x轴交于点A（2，0）．

(1)、求此抛物线的解析式；

(2)、写出顶点坐标及对称轴；

(3)、若抛物线上有一点B，且 $S_{△ O A B}$ ＝8，求点B的坐标．

查看试题解析
24. 学史明理，学史增信，学史崇德，学史力行，在建党100周年之际，某校对全校学生进行了一次党史知识测试，成绩评定共分为A，B，C，D四个等级，随机抽取了部分学生的成绩进行调查，将获得的数据整理绘制成如下两幅不完整的统计图．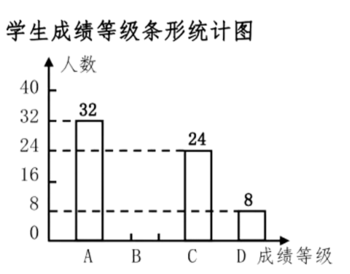
根据统计图提供的信息，解答下列问题：

(1)、在这次调查中一共抽取了名学生；

(2)、请根据以上信息直接在答题卡上补全条形统计图；

(3)、扇形统计图中，D等级对应的圆心角度数是度；

(4)、根据抽样调查的结果，请你估计该校2000学生中有多少名学生的成绩评定为C等级．

查看试题解析
25. 小明一家利用元旦三天驾车到某景点旅游．小汽车出发前油箱有油36L ，行驶，若干小时后，途中在加油站加油若干升，油箱中余油量Q（L）与行驶时间t（h）之间的关系，如图所示，根据图象回答下列问题；

(1)、小汽车行驶小时后加油，中途加油升；

(2)、求加油前邮箱余油量Q与行驶时间t的函数关系式；

(3)、如果小汽车在行驶过程中耗油量速度不变，加油站距景点300km ，车速为80km/h ，要到达目的地，油箱中的油是否够用?请说明理由．

查看试题解析
26. 已知∠ACD＝90°，MN是过点A的直线，AC＝DC，且DB⊥MN于点B，如图易证BD＋AB $＝ \sqrt{2}$ CB，过程如下：
解：过点C作CE⊥CB于点C，与MN交于点E
∵∠ACB＋∠BCD＝90°，∠ACB＋∠ACE＝90°，
∴∠BCD＝∠ACE．
∵DB⊥MN，∴∠ABC＋∠CBD＝90°，
CE⊥CB，∴∠ABC＋∠CEA＝90°，
∴∠CBD＝∠CEA．
又∵AC＝DC，
∴△ACE≌△DCB（AAS），
∴AE＝DB，CE＝CB，
∴△ECB为等腰直角三角形，
∴BE $＝ \sqrt{2}$ CB．
又∵BE＝AE＋AB，∴BE＝BD＋AB，
∴BD＋AB $＝ \sqrt{2}$ CB．

(1)、当MN绕A旋转到如图（2）位置时，BD、AB、CB满足什么样关系式，请写出你的猜想，并给予证明．

(2)、当MN绕A旋转到如图（3）位置时，BD、AB、CB满足什么样关系式，请直接写出你的结论．

查看试题解析
27. 某企业准备购买一批爱心物资捐赠给学校.经了解，若购买洗手液300瓶和口罩200包，则共需6000元；若购买洗手液500瓶和口罩300包，则共需9500元.

(1)、问：每瓶洗手液和每包口罩的价格各是多少元？

(2)、现计划购买洗手液和口罩，若购买这两种物资的总费用不超过11500元，洗手液瓶数和口罩的包数之和为1000，且洗手液的瓶数不大于口罩包数的3倍.设购买洗手液m瓶，购买这两种物资的总费用为W元，请写出W（元）与m（瓶）之间的函数关系式，并求出W的最小值.

查看试题解析
28. 已知：如图，在平面直角坐标系中，点A，B分别在x，y轴上，且OA，OB的长（OA＞OB）是一元二次方程x²﹣7x＋12＝0的两根．

(1)、求点A，B的坐标及线段AB的长；

(2)、过点B作BC⊥AB，交x轴于点C，求点C的坐标；

(3)、在（2）的条件下，如果P，Q分别是线段AB和AC上的动点，连接PQ，设AP＝CQ＝x，问是否存在这样的x，使得△APQ与△ABC相似？若存在，请直接写出x的值；若不存在，请说明理由．

查看试题解析