广东省揭阳市2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. 如图,桌面上放着1个长方体和1个圆柱体,按如图所示的方式摆放在一起,其左视图是( )
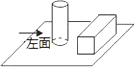 A、
A、 B、
B、 C、
C、 D、
D、 2. 若一元二次方程有一个根为1,则下列等式成立的是( )A、 B、 C、 D、3. 一天晚上,小丽在清洗两只颜色分别为粉色和白色的有盖茶杯时,突然停电了,小丽只好把杯盖和茶杯随机地搭配在一起.则其颜色搭配一致的概率是( )A、 B、 C、 D、14. 中, , 且 , 则A、 B、 C、 D、5. 函数的图象经过(1,-1),则函数的图象是( )A、
2. 若一元二次方程有一个根为1,则下列等式成立的是( )A、 B、 C、 D、3. 一天晚上,小丽在清洗两只颜色分别为粉色和白色的有盖茶杯时,突然停电了,小丽只好把杯盖和茶杯随机地搭配在一起.则其颜色搭配一致的概率是( )A、 B、 C、 D、14. 中, , 且 , 则A、 B、 C、 D、5. 函数的图象经过(1,-1),则函数的图象是( )A、 B、
B、 C、
C、 D、
D、 6. 若 , 则的值为( )A、2 B、 C、 D、97. 点、、在反比例函数的图象上,且 , 则有( )A、 B、 C、 D、8. 如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
6. 若 , 则的值为( )A、2 B、 C、 D、97. 点、、在反比例函数的图象上,且 , 则有( )A、 B、 C、 D、8. 如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( ) A、1:4 B、1:3 C、1:2 D、1:19. 如图所示,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A、1:4 B、1:3 C、1:2 D、1:19. 如图所示,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( ) A、5cosα米 B、米 C、米 D、米10. 如图,将n个边长都为2的正方形按如图所示摆放,点A1 , A2 , …An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )
A、5cosα米 B、米 C、米 D、米10. 如图,将n个边长都为2的正方形按如图所示摆放,点A1 , A2 , …An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )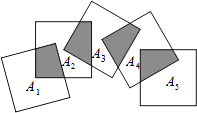 A、n B、n﹣1 C、( )n﹣1 D、 n
A、n B、n﹣1 C、( )n﹣1 D、 n二、填空题
-
11. 若k为整数,关于x的一元二次方程有实数根,则整数k的最大值为 .12. 若点、都在反比例函数的图象上,则m的值是 .13. 如图,矩形中,E是的中点, , , M是线段上的动点,则的最小值是 .
 14. 从长度分别为3,5,6,9的四条线段中任取三条,则能组成三角形的概率为 .
14. 从长度分别为3,5,6,9的四条线段中任取三条,则能组成三角形的概率为 .
15. 如图,△DEF是由△ABC经过位似变换得到的,点O是位似中心, = ,则△DEF与△ABC的面积比是 .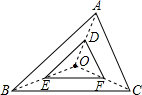 16. 如图,大坝的横截面是一个梯形,坝顶宽 , 坝高 , 斜坡的坡度 , 斜坡的坡度 , 则坡底宽 .
16. 如图,大坝的横截面是一个梯形,坝顶宽 , 坝高 , 斜坡的坡度 , 斜坡的坡度 , 则坡底宽 .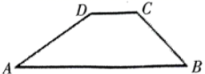 17. 如图,已知矩形OABC的面积为 ,它的对角线OB与双曲线 相交于点D,且OB:OD=5:3,则k=.
17. 如图,已知矩形OABC的面积为 ,它的对角线OB与双曲线 相交于点D,且OB:OD=5:3,则k=.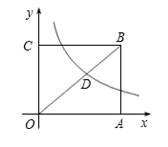
三、解答题
-
18. 计算:19. 画出如图所示物体的主视图、左视图、俯视图.
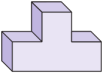 20. 如图:一次函数的图象与反比例函数的图象交于和点 .
20. 如图:一次函数的图象与反比例函数的图象交于和点 . (1)、求点B的坐标;(2)、根据图象回答,当x在什么范围时,一次函数的值大于反比例函数的值.21. 据某市车管部门统计,2013年底全市汽车拥有量为150万辆,而截至到2015年底,全市的汽车拥有量已达216万辆,假定汽车拥有量年平均增长率保持不变.(1)、求年平均增长率;(2)、如果不加控制,该市2017年底汽车拥有量将达多少万辆?22. 如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB= , AD=4.
(1)、求点B的坐标;(2)、根据图象回答,当x在什么范围时,一次函数的值大于反比例函数的值.21. 据某市车管部门统计,2013年底全市汽车拥有量为150万辆,而截至到2015年底,全市的汽车拥有量已达216万辆,假定汽车拥有量年平均增长率保持不变.(1)、求年平均增长率;(2)、如果不加控制,该市2017年底汽车拥有量将达多少万辆?22. 如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB= , AD=4. (1)、求BC的长;(2)、求tan∠DAE的值.23. 已知,在矩形中, , , 动点M从点A出发沿边向点D运动.
(1)、求BC的长;(2)、求tan∠DAE的值.23. 已知,在矩形中, , , 动点M从点A出发沿边向点D运动.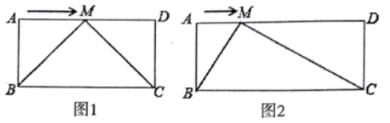 (1)、如图1,当 , 点M运动到边的中点时,请证明;(2)、如图2,当时,点M在运动的过程中,是否存在 , 若存在,请给与证明;若不存在,请说明理由.
(1)、如图1,当 , 点M运动到边的中点时,请证明;(2)、如图2,当时,点M在运动的过程中,是否存在 , 若存在,请给与证明;若不存在,请说明理由.

