安徽省亳州市涡阳县2021-2022学年九年级上学期期末数学试题
试卷更新日期:2022-01-24 类型:期末考试
一、单选题
-
1. -2021的绝对值的相反数是( )A、-2021 B、2021 C、 D、2. 计算的结果是( )A、 B、 C、 D、3. 2020年,引发疫情的冠状病毒被命名为SARS-CoV-2的新型冠状病毒.形态结构冠状病毒粒子呈不规则形状,直径约0.00000022m,用科学记数法表示为( )A、 B、 C、 D、4. 下列分解因式正确的是( )A、 B、 C、 D、5. 已知点关于原点的对称点在一次函数的图象上,则实数k的值为( )A、1 B、-1 C、-2 D、26. 某校九年级(3)班全体学生2021年中考体育模拟考试的成绩统计如表:
成绩(分)
36
40
43
46
48
50
54
人数(人)
2
5
6
7
8
7
5
根据上表中的信息判断,下列结论中错误的是( )
A、该班一共有40名同学 B、该班学生这次考试成绩的众数是48分 C、该班学生这次考试成绩的中位数是47分 D、该班学生这次考试成绩的平均数是46分7. 将关于x的一元二次方程变形为 , 就可以将表示为关于x的一次多项式,从而达到“降次”的目的,又如 , 我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知: , 且 , 则的值为( )A、 B、 C、 D、8. 如图,在中, , 点D为AB边的中点,连接CD,若 , , 则的值为( ) A、 B、 C、 D、9. 二次函数与x轴的两个交点的横坐标分别为m和n,且m <n,则下列结论正确的是( )A、 B、 C、 D、10. 函数的图象如下图所示:其中a、b为常数.由学习函数的经验,可以推断常数、的值满足( )
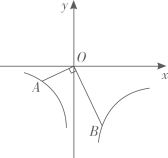
A、 B、 C、 D、9. 二次函数与x轴的两个交点的横坐标分别为m和n,且m <n,则下列结论正确的是( )A、 B、 C、 D、10. 函数的图象如下图所示:其中a、b为常数.由学习函数的经验,可以推断常数、的值满足( ) A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 ,二、填空题
-
11. 计算的结果是12. 计算 的结果是.13. 如图,点A是双曲线 上一动点,连接 ,作 ,且使 ,当点A在双曲线 上运动时,点B在双曲线 上移动,则k的值为.
 14. 矩形ABCD中,E为边AB上一点,将沿DE折叠,使点A的对应点F恰好落在边BC上,连接AF交DE于点N,连接BN.若 , .
14. 矩形ABCD中,E为边AB上一点,将沿DE折叠,使点A的对应点F恰好落在边BC上,连接AF交DE于点N,连接BN.若 , . (1)、矩形ABCD的面积为;(2)、的值为 .
(1)、矩形ABCD的面积为;(2)、的值为 .三、解答题
-
15. 解方程: .16. 如图,在带有网格的平面直角坐标系中,网格边长为一个单位长度,给出了三角形ABC.

⑴作出关于x轴对称的;
⑵以坐标原点为位似中心在图中的网格中作出的位似图形 , 使与的位似比为1:2;
⑶若的面积为3.5平方单位,求出的面积.
17. 观察以下等式:第1个等式:
第2个等式:
第3个等式:
第4个等式:
……
按照以上规律,解决下列问题:
(1)、写出第5个等式:;(2)、写出你猜想的第n个等式:(用含n的等式表示),并证明.18. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?19. 在中, , 斜边 , 过点作 , 以AB为边作菱形ABEF,若 , 求的面积. 20. 小明周末沿着东西走向的公路徒步游玩,在A处观察到电视塔在北偏东37度的方向上,5分钟后在B处观察到电视塔在北偏西53度的方向上.已知电视塔C距离公路AB的距离为300米,求小明的徒步速度.(精确到个位, , , , , , )
20. 小明周末沿着东西走向的公路徒步游玩,在A处观察到电视塔在北偏东37度的方向上,5分钟后在B处观察到电视塔在北偏西53度的方向上.已知电视塔C距离公路AB的距离为300米,求小明的徒步速度.(精确到个位, , , , , , ) 21. 某县教育局组织了一次经典诵读比赛,中学组有两队各10人的比赛成绩如下表:
21. 某县教育局组织了一次经典诵读比赛,中学组有两队各10人的比赛成绩如下表:甲
7
8
9
7
10
10
9
10
10
10
乙
10
8
7
9
8
10
10
9
10
9
(1)、甲队成绩的中位数是分,乙队成绩的众数是分;(2)、计算乙队的平均成绩;(3)、如果要从两个队中选择一对参加市级比赛,你认为安排哪个队更容易获奖.22. 一大型商场经营某种品牌商品,该商品的进价为每件30元,根据市场调查发现,该商品每周的销售量y(件)与售价x(元件)(x为正整数)之间满足一次函数关系,下表记录的是某三周的有关数据:x(元/件)
40
50
60
y(件)
10000
9500
9000
(1)、求y与x的函数关系式(不求自变量的取值范围);(2)、在销售过程中要求销售单价不低于成本价,且不高于150元/件.若某一周该商品的销售量不少于6000件,求这一周该商场销售这种商品获得的最大利润和售价分别为多少元?(3)、抗疫期间,该商场这种商品售价不大于150元/件时,每销售一件商品便向某慈善机构捐赠m元 , 捐赠后发现,该商场每周销售这种商品的利润仍随售价的增大而增大.请求出m的取值范围.23. 已知如图是锐角三角形,分别以边AB、AC为边向外作和 , 和均为等边三角形,且BE和CD交于点F,连接AF.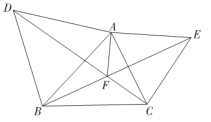 (1)、求证:;(2)、求出的度数;(3)、求证: .
(1)、求证:;(2)、求出的度数;(3)、求证: .