黑龙江省双鸭山市集贤县2020-2021学年九年级上学期期末数学试题

试卷更新日期：2022-01-24 类型：期末考试

进入出卷网下载

一、填空题

1. 点A（a，3）与点B（﹣4，b）关于原点对称，则a+b＝.

查看试题解析
2. 若二次函数 $y = (a - 1) x^{2} - 4 x + 2$ 的图象与x轴有且只有一个交点，则a的值为．

查看试题解析
3. 学校组织团员同学参加实践活动，共安排2辆车，小王和小李随机上了一辆车，结果他们同车的概率是．

查看试题解析
4. 一个圆锥的侧面积是底面积的2倍，则圆锥侧面展开图扇形的圆心角是．

查看试题解析
5. 如图，AB为⊙O的直径，弦CD⊥AB于E，已知CD＝12，BE＝2，则⊙O半径为．

查看试题解析
6. 如图，某单位准备将院内一块长30m，宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道，剩余的地方种植花草，如图，要使种植花草的面积为532m² ，设小道进出口的宽度为x m，根据条件，可列出方程：．

查看试题解析
7. 如图，BD为正方形ABCD的对角线，BE平分∠DBC，交DC与点E，将△BCE绕点C顺时针旋转90°得到△DCF，若CE＝1 cm，则BF＝cm.

查看试题解析
8. 半径为3cm的圆内有长为 $3 \sqrt{3} c m$ 的弦，则此弦所对的圆周角的度数为．

查看试题解析
9. 设m，n分别为一元二次方程 $x^{2} + 2 x - 2021 = 0$ 的两个实数根，则 $m^{2} + 3 m + n =$ ．

查看试题解析
10. 如下图，在平面直角坐标系中有一边长为l的正方形OABC，边OA、OC分别在x轴、y 轴上，如果以对角线OB为边作第二个正方形OBB₁C₁ ，再以对角线OB_l为边作第三个正方形OB_lB₂C₂ ，照此规律作下去，则点B₂₀₂₀的纵坐标为。

查看试题解析

二、单选题

11. 下列图形中既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
12. 已知方程x²+bx+a＝0有一个根是﹣a（a≠0），则下列代数式的值恒为常数的是（　　）

A、ab B、 $\frac{a}{b}$ C、a+b D、a﹣b

查看试题解析
13. 抛物线 $y = - 3 {(x + 1)}^{2} - 2$ 经过平移得到抛物线 $y = - 3 x^{2}$ ，平移的方法是（）

A、向左平移1个单位，再向下平移2个单位 B、向右平移1个单位，再向下平移2个单位 C、向左平移1个单位，再向上平移2个单位 D、向右平移1个单位，再向上平移2个单位

查看试题解析
14. 如图，AB为⊙O的直径，点C为⊙O上的一点，过点C作⊙O的切线，交直径AB的延长线于点D；若∠A＝23°，则∠D的度数是（）

A、23° B、44° C、46° D、57°

查看试题解析
15. 二次函数y＝ax²+bx+c（a≠0）与一次函数y＝ax+c在同一坐标系中的图象大致为（）

A、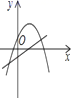 B、 C、 D、

查看试题解析
16. 若关于 $x$ 的方程 $k x^{2} - 2 x + \frac{1}{4} = 0$ 有实数根，则实数 $k$ 的取值范围是（）

A、 $k < 4$ B、 $k < 4$ 且 $k \neq 0$ C、 $k \leq 4$ D、 $k \leq 4$ 且 $k \neq 0$

查看试题解析
17. 在直角坐标系中，等腰直角三角形AOB在如图所示的位置，点B的横坐标为2，将△AOB绕点O按逆时针方向旋转90°，得到△A′OB′，则点A′的坐标为（）

A、（1，1） B、（ $\sqrt{2}$ ， $\sqrt{2}$ ） C、（﹣1，1） D、（﹣ $\sqrt{2}$ ， $\sqrt{2}$ ）

查看试题解析
18. 已知二次函数y＝（a﹣1）x²﹣x+a²﹣1图象经过原点，则a的取值为（　　）

A、a＝±1 B、a＝1 C、a＝﹣1 D、无法确定

查看试题解析
19. 某航空公司有若干个飞机场，每两个飞机场之间都开辟一条航线，一共开辟了10条航线，则这个航空公司共有飞机场（）

A、4个 B、5个 C、6个 D、7个

查看试题解析
20. 如图，二次函数y＝ax²＋bx＋c(a≠0)的图象与x轴交于A，B两点，与y轴交于点C，且OA＝OC．则下列结论：①abc＜0；② $\frac{b^{2} - 4 a c}{4 a} > 0$ ；③ac－b＋1＝0；④OA·OB＝ $- \frac{c}{a}$ .其中正确结论的个数是（）

A、4 B、3 C、2 D、1

查看试题解析

三、解答题

21. 如图；在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度，已知 $△ A B C$ ：
⑴作出 $△ A B C$ 关于点O成中心对称的图形 $△ A_{1} B_{1} C_{1}$ ，写出点B对应点 $B_{1}$ 的坐标．
⑵作出把 $△ A B C$ 绕点A逆时针旋转90°后的图形 $△ A_{2} B_{2} C_{2}$ ．并求出AB在上述旋转过程中所扫过的面积．

查看试题解析
22. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 54 °$ ，以AB为直径的 $⊙ O$ 分别交AC、BC于点D、E，过点B作直线BF，交AC的延长线于点F．

(1)、求证： $B E = C E$ ；

(2)、若 $A B = 6 c m$ ，则弧DE的长是．

(3)、当 $∠ F$ 的度数是多少时，BF与 $⊙ O$ 相切，证明你的结论．

查看试题解析
23. （2016新疆）某校在民族团结宣传活动中，采用了四种宣传形式：A唱歌，B舞蹈，C朗诵，D器乐．全校的每名学生都选择了一种宣传形式参与了活动，小明对同学们选用的宣传形式，进行了随机抽样调查，根据调查统计结果，绘制了如图两种不完整的统计图表：
选项
方式
百分比
A
唱歌
35%
B
跳舞
a
C
朗诵
25%
D
器乐
30%
请结合统计图表，回答下列问题：

(1)、本次调查的学生共人，a= ，并将条形统计图补充完整；

(2)、如果该校学生有2000人，请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人？

(3)、学校采用调查方式让每班在A、B、C、D四种宣传形式中，随机抽取两种进行展示，请用树状图或列表法，求某班抽到的两种形式恰好是“唱歌”和“舞蹈”的概率．

查看试题解析
24. 某口罩生产厂生产的口罩1月份平均日产量为20000，1月底因突然爆发新冠肺炎疫情，市场对口罩需求量大增，为满足市场需求，工厂决定从2月份起扩大产能，3月份平均日产量达到24200个．

(1)、求口罩日产量的月平均增长率；

(2)、按照这个增长率，预计4月份平均日产量为多少？

查看试题解析
25. 已知 $△ A B C$ 与 $△ D E C$ 是两个大小不同的等腰直角三角形．

(1)、如图1所示，连接AE，DB，则线段AE和DB的数量关系和位置关系分别是：（请直接写出结论）

(2)、如图2所示，连接DB，将线段DB绕D点顺时针旋转90°到DF，连接AF，请写出线段DE和AF的关系，并说明理由．

查看试题解析
26. 已知，如图，二次函数y=ax²+bx+c的图象与x轴交于A、B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．

(1)、求抛物线的解析式；

(2)、求△MCB的面积．

查看试题解析
27. 某商品的进价为每件50元．当售价为每件70元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：

(1)、若设每件降价x元、每星期售出商品的利润为y元，请写出y与x的函数关系式，并求出自变量x的取值范围；

(2)、当降价多少元时，每星期的利润最大？最大利润是多少？

查看试题解析

选项	方式	百分比
A	唱歌	35%
B	跳舞	a
C	朗诵	25%
D	器乐	30%